模型设计

• First, we must define an embedding function that maps discrete text into a continuous space.
• Second, we require a rounding method to map vectors in embedding space back to words.

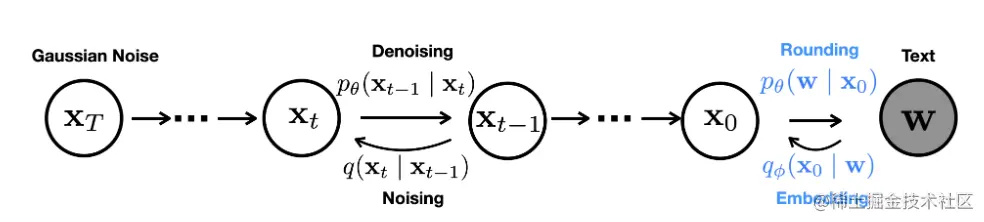
端到端训练

为了将离散文本应用到连续扩散模型上，这里设置了一个embedding函数$\mathrm E_{\mathrm{MB}}(w_i)$将每个词映射到词向量$\mathbb{R}^d$。对于长度为$n$的序列$\mathbf w$：

作者在实验中发现，使用预训练的word embedding效果不如使用随机高斯噪声初始化之后训练出来的embedding，所以加了这样一个网络，实现离散词序列$\mathbf w$到$\mathbf x_0$的马尔科夫转换，参数化为：

与之对应的反向过程添加了一个可训练的舍入步骤，参数化为：

其中$p_\theta\left(w_i \mid x_i\right)$是一个softmax分布。

因为增加了一个嵌入步骤和一个舍入步骤，添加的这两个网络是和扩散模型进行联合训练的，因此要对训练目标函数改进：

$\mathcal{L}_{\mathrm{simple}}^{\mathrm{e} 2 \mathrm{e}}(\mathbf{w})$是$\mathcal{L}_{\mathrm{vlb}}^{\mathrm{e} 2 \mathrm{e}}(\mathbf{w})$的简化版，是根据DDPM设计的目标函数。

DDPM的目标函数：

可视化之后可以看到学到的embedding是有意义的。

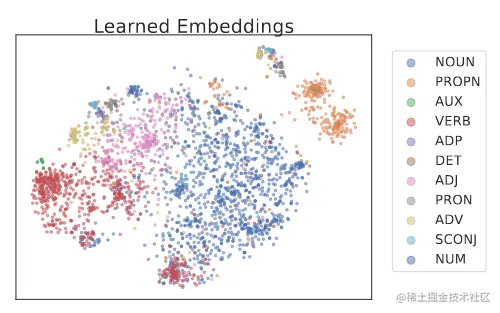
减少舍入误差

embedding是将离散文本映射到连续的$\mathbf x_0$上，那与之对应的反向过程就应该是将模型预测出来的$\mathbf x_0$转换回离散的文本。

舍入步骤是根据$\operatorname{argmax} p_\theta\left(\mathbf{w} \mid \mathbf{x}_0\right)=\prod_{i=1}^n p_\theta\left(w_i \mid x_i\right)$选择每个位置上可能性最大的词。理想状态下通过这个舍入步骤就可以将模型输出的$\mathbf x_0$映射回离散文本，因为去噪步骤应该能让$\mathbf x_0$恰好回到某个单词的embedding上。

然而实际情况是不行的，模型输出是不会精确到某个单词的embedding。

作者认为造成上述问题的原因，是在目标函数中$\mathcal{L}_{\mathrm{simple}}^{\mathrm{e} 2 \mathrm{e}}(\mathbf{\mathbf x_0})$对$\mathbf x_0$结构的建模不够重视。

其中的$\mu_\theta\left(\mathrm{x}_t, t\right)$网络直接去预测时间步$t$去噪的$p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)$的均值。$\mathbf x_0$对单词的约束只会出现在$t$接近于0的项中。因此需要对目标函数进行调整，去强调$\mathbf x_0$。

作者对$\mathcal{L}_{\text {simple }}$进行调整，强调模型在目标函数的每一项中都去显式地建模$\mathbf x_0$。 作者推导出一个类似于$\mathcal{L}_{\text {simple }}$的使用$\mathbf x_0$参数化的公式：

其中网络$f_\theta\left(\mathbf{x}_t, t\right)$直接去预测$\mathbf x_0$，这样会让神经网络去预测每一项的$\mathbf x_0$。 使用修改之后的目标去训练模型，模型很快就会学到让$\mathbf x_0$能回到以word embedding为中心。

clamping trick

作者将其称为clamping trick，在clamping trick中，模型将$\mathbf x_t$降噪为$\mathbf x_{t-1}$的生成过程：

1. 通过$f_\theta (\mathbf x_t,t)$估计出一个$\mathbf x_0$

2. 在这个估计的条件相爱对$\mathbf x_{t-1}$进行采样

3. $\mathbf{x}_{t-1}=\sqrt{\bar{\alpha}} f_\theta\left(\mathbf{x}_t, t\right)+\sqrt{1-\bar{\alpha}} \epsilon$ 其中$\bar{\alpha}_t=\prod_{s=0}^t\left(1-\beta_s\right)$， $\epsilon \sim \mathcal{N}(0, I)$

   这一步就是用的DDPM中的那个，因为都是高斯核，所以$\mathbf x_t$可以由$\mathbf x_0$一步得到。

   $\begin{aligned} \boldsymbol{x}_t & =\sqrt{\alpha_t} x_{t-1}+\sqrt{1-\alpha_t} \epsilon_{t-1}^* \\ & =\sqrt{\alpha_t}\left(\sqrt{\alpha_{t-1}} x_{t-2}+\sqrt{1-\alpha_{t-1}} \epsilon_{t-2}^*\right)+\sqrt{1-\alpha_t} \epsilon_{t-1}^* \\ & =\sqrt{\alpha_t \alpha_{t-1}} x_{t-2}+\sqrt{\alpha_t-\alpha_t \alpha_{t-1}} \epsilon_{t-2}^*+\sqrt{1-\alpha_t} \epsilon_{t-1}^* \\ & =\sqrt{\alpha_t \alpha_{t-1}} x_{t-2}+\sqrt{{\sqrt{\alpha_t-\alpha_t \alpha_{t-1}}}^2+\sqrt{1-\alpha_t^2}} \epsilon_{t-2} \\ & =\sqrt{\alpha_t \alpha_{t-1}} x_{t-2}+\sqrt{\alpha_t-\alpha_t \alpha_{t-1}+1-\alpha_t} \epsilon_{t-2} \\ & =\sqrt{\alpha_t \alpha_{t-1}} x_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}} \epsilon_{t-2} \\ & =\ldots \\ & =\sqrt{\prod_{i=1}^t \alpha_i} x_0+\sqrt{1-\prod_{i=1}^t \alpha_i} \epsilon_0 \\ & =\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon_0\end{aligned}$

clamping trick 会将网络$f_\theta (\mathbf x_t,t)$的预测结果映射到接近的word embedding 序列上。 现在采样步骤就变为了：

clamping trick 迫使扩散模型降噪过程中每一步都去计算一个word embedding，使向量预测更为准确，以此减少舍入误差。

作者在这里提示将开始使用clamping trick的起始位置设置为超参数。具体原因看论文P5。

论文信息

论文地址：[2205.14217] Diffusion-LM Improves Controllable Text Generation (arxiv.org)

代码地址：XiangLi1999/Diffusion-LM: Diffusion-LM (github.com)

---

本文正在参加「金石计划」