开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 32 天，点击查看活动详情

在简单易学的机器学习算法——马尔可夫链蒙特卡罗方法MCMC中简单介绍了马尔可夫链蒙特卡罗MCMC方法的基本原理，介绍了Metropolis采样算法的基本过程，这一部分，主要介绍Metropolis-Hastings采样算法，Metropolis-Hastings采样算法也是基于MCMC的采样算法，是Metropolis采样算法的推广形式。

1. Metropolis-Hastings算法的基本原理

1.1. Metropolis-Hastings算法的基本原理

与Metropolis采样算法类似，假设需要从目标概率密度函数$p\left ( \theta \right )$中进行采样，同时，$\theta$满足$-\infty <\theta <\infty$。Metropolis-Hastings采样算法根据马尔可夫链去生成一个序列：

其中，$\theta ^{\left (t \right )}$表示的是马尔可夫链在第$t$代时的状态。

在Metropolis-Hastings采样算法的过程中，首先初始化状态值$\theta ^{\left (1 \right )}$，然后利用一个已知的分布$q\left ( \theta \mid \theta ^{\left ( t-1 \right )} \right )$生成一个新的候选状态$\theta ^{\left (\ast \right )}$，随后根据一定的概率选择接受这个新值，或者拒绝这个新值，与Metropolis采样算法不同的是，在Metropolis-Hastings采样算法中，概率为：

这样的过程一直持续到采样过程的收敛，当收敛以后，样本$\theta ^{\left (t \right )}$即为目标分布$p\left ( \theta \right )$中的样本。

1.2. Metropolis-Hastings采样算法的流程

基于以上的分析，可以总结出如下的Metropolis-Hastings采样算法的流程：

• 初始化时间$t=1$
• 设置$u$的值，并初始化初始状态$\theta ^{\left (t \right )}=u$
• 重复以下的过程：
  • 令$t=t+1$
  • 从已知分布$q\left ( \theta \mid \theta ^{\left ( t-1 \right )} \right )$中生成一个候选状态$\theta ^{\left (\ast \right )}$
  • 计算接受的概率：$\alpha =min\: \left ( 1,\; \frac{p\left ( \theta ^{\left ( \ast \right )} \right )}{p\left ( \theta ^{\left ( t-1 \right )} \right )} \frac{q\left ( \theta ^{\left ( t-1 \right )}\mid \theta ^{\left ( \ast \right )} \right )}{q\left ( \theta ^{\left ( \ast \right )} \mid \theta ^{\left ( t-1 \right )} \right )}\right )$
  • 从均匀分布$Uniform\left ( 0, 1 \right )$生成一个随机值$a$
  • 如果$a\leqslant \alpha$，接受新生成的值：$\theta ^{\left (t \right )}=\theta ^{\left (\ast \right )}$；否则：$\theta ^{\left (t \right )}=\theta ^{\left (t-1 \right )}$
• 直到$t=T$

1.3. Metropolis-Hastings采样算法的解释

与Metropolis采样算法类似，要证明Metropolis-Hastings采样算法的正确性，最重要的是要证明构造的马尔可夫过程满足如上的细致平稳条件，即：

对于上面所述的过程，分布为$p\left ( \theta \right )$，从状态$i$转移到状态$j$的转移概率为：

其中，$Q_{i,j}$为上述已知的分布，$Q_{i,j}$为：

在Metropolis-Hastings采样算法中，并不要求像Metropolis采样算法中的已知分布为对称的。

接下来，需要证明在Metropolis-Hastings采样算法中构造的马尔可夫链满足细致平稳条件。

因此，通过以上的方法构造出来的马尔可夫链是满足细致平稳条件的。

1.4. 实验1

如前文的Metropolis采样算法，假设需要从柯西分布中采样数据，我们利用Metropolis-Hastings采样算法来生成样本，其中，柯西分布的概率密度函数为：

那么，根据上述的Metropolis-Hastings采样算法的流程，接受概率$\alpha$的值为：

若已知的分布符合条件独立性，则

此时，与Metropolis采样算法一致。

2. 多变量分布的采样

上述的过程中，都是针对的是单变量分布的采样，对于多变量的采样，Metropolis-Hastings采样算法通常有以下的两种策略：

• Blockwise Metropolis-Hastings采样
• Componentwise Metropolis-Hastings采样

2.1. Blockwise Metropolis-Hastings采样

对于BlockWise Metropolis-Hastings采样算法，在选择已知分布时，需要选择与目标分布具有相同维度的分布。针对上述的更新策略，在BlockWise Metropolis-Hastings采样算法中采用的是向量的更新策略，即：$\Theta =\left ( \theta _1,\theta _2,\cdots ,\theta _N \right )$。因此，算法流程为：

• 初始化时间$t=1$
• 设置$\mathbf{u}$的值，并初始化初始状态$\Theta ^{\left (t \right )}=\mathbf{u}$
• 重复以下的过程：
  • 令$t=t+1$
  • 从已知分布$q\left ( \Theta \mid \Theta ^{\left ( t-1 \right )} \right )$中生成一个候选状态$\Theta ^{\left (\ast \right )}$
  • 计算接受的概率：$\alpha =min\: \left ( 1,\; \frac{p\left ( \Theta ^{\left ( \ast \right )} \right )}{p\left ( \Theta ^{\left ( t-1 \right )} \right )} \frac{q\left ( \Theta ^{\left ( t-1 \right )}\mid \Theta ^{\left ( \ast \right )} \right )}{q\left ( \Theta ^{\left ( \ast \right )} \mid \Theta ^{\left ( t-1 \right )} \right )}\right )$
  • 从均匀分布$Uniform\left ( 0, 1 \right )$生成一个随机值$a$
  • 如果$a\leqslant \alpha$，接受新生成的值：$\Theta ^{\left (t \right )}=\Theta ^{\left (\ast \right )}$；否则：$\Theta ^{\left (t \right )}=\Theta ^{\left (t-1 \right )}$
• 直到$t=T$

2.2. Componentwise Metropolis-Hastings采样

对于上述的BlockWise Metropolis-Hastings采样算法，有时很难找到与所要采样的分布具有相同维度的分布，因此可以采用Componentwise Metropolis-Hastings采样，该采样算法每次针对一维进行采样，其已知分布可以采用单变量的分布，算法流程为：

• 初始化时间$t=1$
• 设置$\mathbf{u}=\left ( u_1,u_2,\cdots ,u_N \right )$的值，并初始化初始状态$\Theta ^{\left (t \right )}=\mathbf{u}$
• 重复以下的过程：
  • 令$t=t+1$
  • 对每一维：$i=1,2,\cdots N$
    • 从已知分布$q\left ( \theta _i\mid \theta _i^{\left ( t-1 \right )} \right )$中生成一个候选状态$\theta _i^{\left (\ast \right )}$，假设没有更新之前的整个向量为：$\Theta ^{\left (t-1 \right )}=\left ( \theta _1^{\left ( t-1 \right )},\cdots ,\theta _i^{\left ( t-1 \right )},\cdots ,\theta _N^{\left ( t-1 \right )} \right )$，更新之后的向量为：$\Theta =\left ( \theta _1^{\left ( t-1 \right )},\cdots ,\theta _i^{\left ( \ast \right )},\cdots ,\theta _N^{\left ( t-1 \right )} \right )$
    • 计算接受的概率：$\alpha =min\: \left ( 1,\; \frac{p\left ( \Theta \right )}{p\left ( \Theta ^{\left ( t-1 \right )} \right )} \frac{q\left ( \theta _i^{\left ( t-1 \right )}\mid \theta _i^{\left ( \ast \right )} \right )}{q\left ( \theta _i^{\left ( \ast \right )} \mid \theta _i^{\left ( t-1 \right )} \right )}\right )$
    • 从均匀分布$Uniform\left ( 0, 1 \right )$生成一个随机值$a$
    • 如果$a\leqslant \alpha$，接受新生成的值：$\theta _i^{\left (t \right )}=\theta _i^{\left (\ast \right )}$；否则：$\theta _i^{\left (t \right )}=\theta _i^{\left (t-1 \right )}$
• 直到$t=T$

2.3. 实验

假设希望从二元指数分布：

中进行采样，其中，假设$\theta _1$和$\theta _2$在区间$\left [ 0,8 \right ]$，$\lambda _1 = 0.5$，$\lambda _2 = 0.1$， $\lambda = 0.01$，$max\left ( \theta _1,\theta _2 \right )=8$。

2.3.1. Blockwise

实验代码

'''
Date:20160703
@author: zhaozhiyong
'''
import random
import math
from scipy.stats import norm
import matplotlib.pyplot as plt

def bivexp(theta1, theta2):
    lam1 = 0.5
    lam2 = 0.1
    lam = 0.01
    maxval = 8
    y = math.exp(-(lam1 + lam) * theta1 - (lam2 + lam) * theta2 - lam * maxval)
    return y

T = 5000
sigma = 1
thetamin = 0
thetamax = 8
theta_1 = [0.0] * (T + 1)
theta_2 = [0.0] * (T + 1)
theta_1[0] = random.uniform(thetamin, thetamax)
theta_2[0] = random.uniform(thetamin, thetamax)

t = 0
while t < T:
    t = t + 1
    theta_star_0 = random.uniform(thetamin, thetamax)
    theta_star_1 = random.uniform(thetamin, thetamax)
    # print theta_star
    alpha = min(1, (bivexp(theta_star_0, theta_star_1) / bivexp(theta_1[t - 1], theta_2[t - 1])))
        
    u = random.uniform(0, 1)
    if u <= alpha:
        theta_1[t] = theta_star_0
        theta_2[t] = theta_star_1
    else:
        theta_1[t] = theta_1[t - 1]
        theta_2[t] = theta_2[t - 1]
plt.figure(1)
ax1 = plt.subplot(211)
ax2 = plt.subplot(212)        
plt.ylim(thetamin, thetamax)
plt.sca(ax1)
plt.plot(range(T + 1), theta_1, 'g-', label="0")
plt.sca(ax2)
plt.plot(range(T + 1), theta_2, 'r-', label="1")
plt.show()

plt.figure(2)
ax1 = plt.subplot(211)
ax2 = plt.subplot(212)        
num_bins = 50
plt.sca(ax1)
plt.hist(theta_1, num_bins, normed=1, facecolor='green', alpha=0.5)
plt.title('Histogram')
plt.sca(ax2)
plt.hist(theta_2, num_bins, normed=1, facecolor='red', alpha=0.5)
plt.title('Histogram')
plt.show()

实验结果

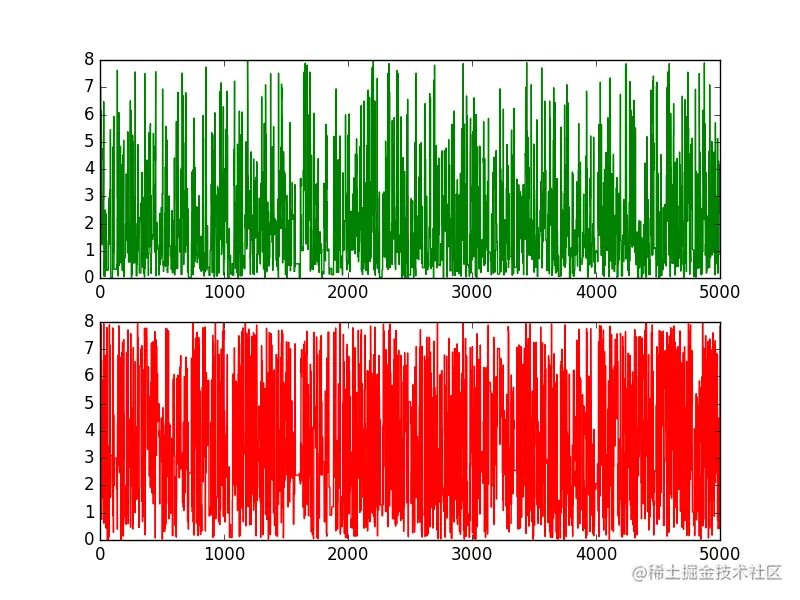
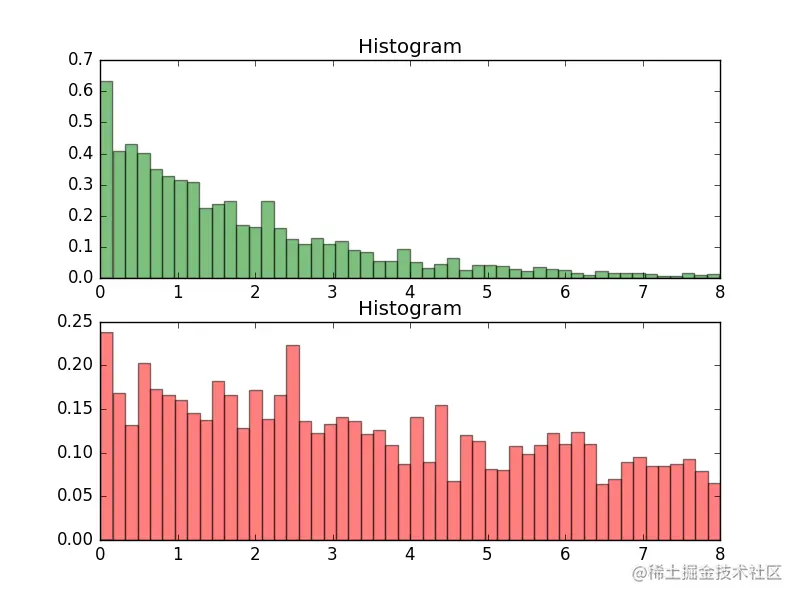
2.3.2. Componentwise

实验代码

'''
Date:20160703
@author: zhaozhiyong
'''
import random
import math
from scipy.stats import norm
import matplotlib.pyplot as plt

def bivexp(theta1, theta2):
    lam1 = 0.5
    lam2 = 0.1
    lam = 0.01
    maxval = 8
    y = math.exp(-(lam1 + lam) * theta1 - (lam2 + lam) * theta2 - lam * maxval)
    return y

T = 5000
sigma = 1
thetamin = 0
thetamax = 8
theta_1 = [0.0] * (T + 1)
theta_2 = [0.0] * (T + 1)
theta_1[0] = random.uniform(thetamin, thetamax)
theta_2[0] = random.uniform(thetamin, thetamax)

t = 0
while t < T:
    t = t + 1
    # step 1
    theta_star_1 = random.uniform(thetamin, thetamax)
    alpha = min(1, (bivexp(theta_star_1, theta_2[t - 1]) / bivexp(theta_1[t - 1], theta_2[t - 1])))
        
    u = random.uniform(0, 1)
    if u <= alpha:
        theta_1[t] = theta_star_1
    else:
        theta_1[t] = theta_1[t - 1]
    
    # step 2
    theta_star_2 = random.uniform(thetamin, thetamax)
    alpha = min(1, (bivexp(theta_1[t], theta_star_2) / bivexp(theta_1[t], theta_2[t - 1])))
    u = random.uniform(0, 1)
    if u <= alpha:
        theta_2[t] = theta_star_2
    else:
        theta_2[t] = theta_2[t - 1]
        
plt.figure(1)
ax1 = plt.subplot(211)
ax2 = plt.subplot(212)        
plt.ylim(thetamin, thetamax)
plt.sca(ax1)
plt.plot(range(T + 1), theta_1, 'g-', label="0")
plt.sca(ax2)
plt.plot(range(T + 1), theta_2, 'r-', label="1")
plt.show()

plt.figure(2)
ax1 = plt.subplot(211)
ax2 = plt.subplot(212)        
num_bins = 50
plt.sca(ax1)
plt.hist(theta_1, num_bins, normed=1, facecolor='green', alpha=0.5)
plt.title('Histogram')
plt.sca(ax2)
plt.hist(theta_2, num_bins, normed=1, facecolor='red', alpha=0.5)
plt.title('Histogram')
plt.show()

实验结果

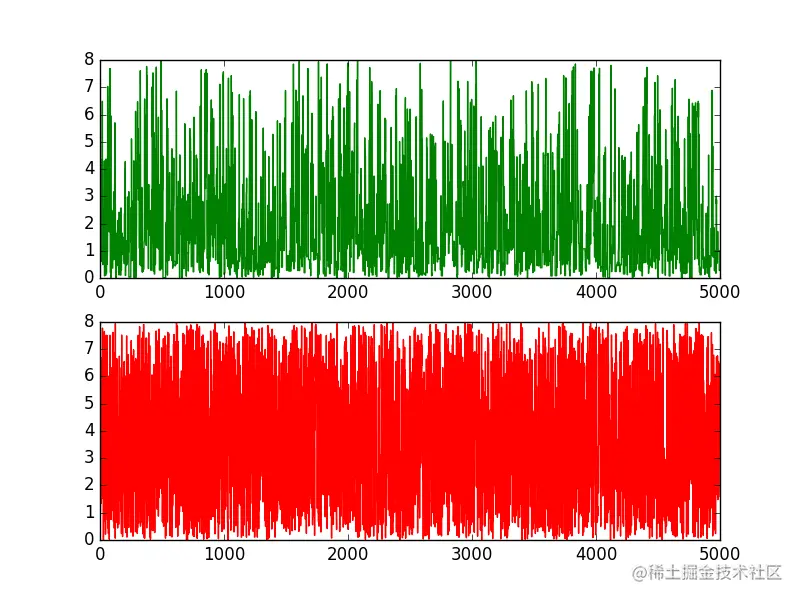
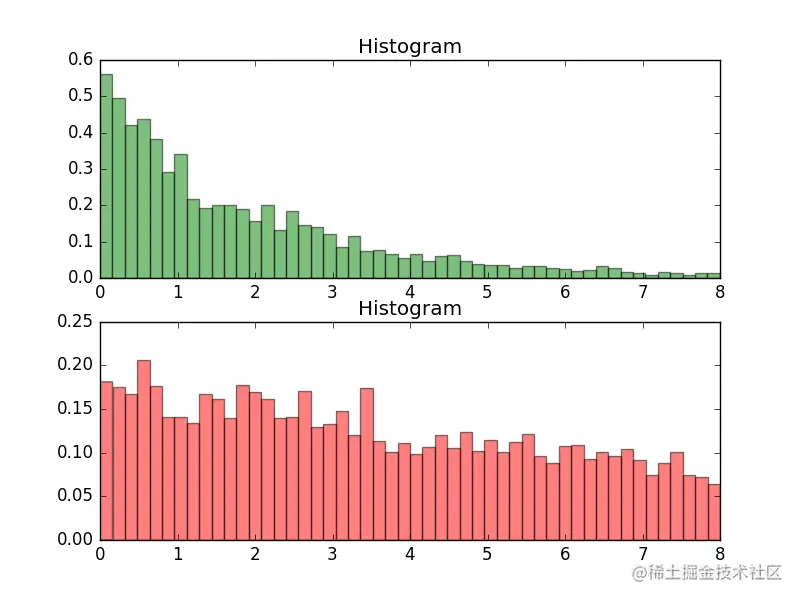
开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 32 天，点击查看活动详情