基本概念：凸集、凸函数、凸优化问题

凸集

definition

$x,y\in C \subseteq R^n \rightarrow \forall 0\le t\le 1, tx + (1-t)y\in C$

$x$，$y$是任取的某一特定对。

凸组合构成凸包

$\forall x_1,...,x_k \in C, C'=\sum_{i=1}^k \theta_i x_k$ with $\theta_i \ge 0$ and $\sum_{i=1}^k \theta_i=1$。$C'$构成凸包convex hull，即所有点凸组合构成的集合。凸包也是包含非凸区域的最小凸区域。

常见的凸集类型如下

• Norm ball: $\{x: ||x||\le r\}$
• 椭球：$\{x: (x-x_c)^TP^{-1}(x-x_c)\le 1\}$,P是对称正定阵
• Hyperplane: $\{x: a^Tx=b\}$, a是平面法向量
• Halfspace: $\{x: a^Tx\le b\}$
• Affine space: $\{x: Ax=b\}$
• polyhedron: $\{x: Ax\le b\}$ 若干平面方程的交集，如果是$Ax\le b, Cx= d$也是多边形，因为$Cx=d$可以转化成$Cx\le d, -Cx\le -d$，然后和前面合并在一起即可。
• simplex: 特殊的多边形，可以组成是不同维度空间中的complex（复形），一个经典的单纯形是概率单纯形，即n个元素，非负且和为0。
• cone: $x\in C\rightarrow tx\in C \forall t \ge 0$
• convex cone: $x_1,x_2\in C\rightarrow t_1x_1+t_2x_2\in C\forall t_1,t_2\ge 0$
• conic combination: $x_1,...,x_k\in R^n, C'=\sum_{i=1}^k\theta_k x_k, \theta_i \ge 0$
• norm cone: $\{(x,t): ||x||\le t\}$，想象一个圆锥，每固定一个t就形成一个圆面。
• normal cone: $N_C(x)=\{g: g^Tx\ge g^Ty, \forall y \in C\}, x\in C$，这里C不一定是凸集也ok
• positive semidefinite cone: $S_n^+$，表示所有n阶半正定对称方阵。这是一个convex cone，可以自行验证

性质

• separating hyperplane theorem：两个不相交的convex set存在一个超平面划分
• Supporting hyperplane theorem：非空凸集存在支撑。啥叫支撑？就是说对于一个边界上的点$x_0\in C$，一定存在一个向量$a$，满足$\forall x \in C, a^Tx \le a^Tx_0$

凸集操作

• 求交集保凸性
• 线性变换aX+b保凸，这里a和b都是实数
• affine保凸，Ax+b，这里A是矩阵，b是向量。并且如果A可逆，那么像凸则原像也是凸的
• 数字除法保凸，$\frac{Ax+b}{c^Tx+d}$也保凸。

第三个性质有个很妙的题目：如何证明下面的矩阵不等式的解集是凸集？
$x_1A_1+...+x_kA_k\le B$，A和B都是n阶方阵。不等号表示正定性。
一个naive的方法是直接用定义去证明。还有一个更骚的，构造$f(x)=B-\sum_kx_kA_k$，他的输入是不等式的解，输出是一个n阶正定阵，那么这是一个affine变换，并且像是正定方阵是convex cone，肯定是凸的，所以原像也是凸的。

凸函数

definition

$f: R^n\rightarrow R, s.t. \forall x,y\in dom(f),\forall 0\le t\le 1, f(tx+(1-t)y)\le tf(x)+(1-t)f(y)$

Jessen不等式，下凸

严格凸：等号取不到。但是注意，这个只能说等号取不到是严格凸，反过来不成立，比如$x^4$严格凸，但是在0处二阶导为0。对于二次型，严格凸和矩阵正定是等价的。 强凸：$m > 0, f-\frac{m}{2}||x||_2^2$是凸的，即至少和二次函数一样凸

凸函数有个好处，如果我们让dom之外的部分取值都是$\infty$，那它还是凸的，这样我们其实直接延拓一个新的函数即不需要再考虑定义域。

案例

• 二次型$x^TQx+b^Tx+c$，Q半正定时为凸
• square error: $(y-Ax)^T(y-Ax)$，就是二次型，对应的$Q=A^TA$始终半正定
• norm函数$||x||_p=(\sum x^p)^{1/p}$
• max函数
• 支撑函数:$I^*_C(x)=\max_{y\in C} x^Ty$
• logdet(X)，在正定对称阵上是凹函数。
• 几何平均：$(\prod_i x_i^p)^{1/p}$是凹函数

性质

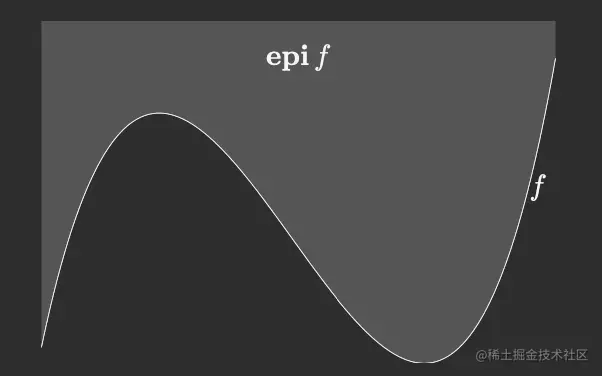
• 凸函数等价于他的epigraph是凸的:$epi(f)=\{(x,t)\in dom(f)\times R: f(x)\le t\}$ 这里其实是把凸函数看作是一个集合的边界。相应的概念叫$hypo(f)=\{(x,t)\in dom(f)\times R: f(x)\ge t\}$

几何解释
一个凸函数$f(x)$，如果一阶可微，那么$f(y)\ge f(x)+\nabla^T f(x)(y-x)$，而他的epigraph为$t\ge f(y)$，因此，$(y,t)$满足$t\ge f(y)\ge f(x)+\nabla^T f(x)(y-x)$。这个东西可以转化成$[\nabla f(x),-1]([y,t]^T-[x, f(x)]^T)\le 0$。这说明，在f(x)上任取x处的超平面支撑了epigraph。

• 凸函数则sublevel sets是凸的：$\{x\in dom(f): f\le t\}, \forall t\in R$ （反过来不成立，$-e^x$）
• 如果一阶可微，那么f是凸的等价于$dom(f)$凸且$f(y)\ge f(x)+\nabla f(x)^T(y-x),\forall x,y$（切线在下）
• 如果2阶可微，那么f是凸的等价于$dom(f)$凸且$\nabla^2f(x)\ge 0$，这里不等号表示半正定

Schur补条件：考虑一个n阶对称阵，如果可以分块2x2$[[A,B],[B^T,D]]$并且$det(A)\ne0$，对角线上的两个阵是方阵，那么Schur补就是$S=D-B^TA^{-1}B$。X正定等价于S和A正定。并且$det(X)=det(A)det(S)$

保凸操作

• 一些列凸函数的非负线性组合
• 对一系列凸函数取最大值
• 偏最小值，$g(x,y)$是凸的，$f(x)=\min_{y\in C}g(x,y)$是凸函数。
• affine保凸：f是convex，$f(Ax+b)$是凸的
• 复合变换：利用链式求二阶导判断正负。
• log-sum-exp：$g(x)=\log(\sum_{i=1}^k e^{a_i^T x+b_i})$,softmax

共轭函数

定义

对于函数$f(x)$，其共轭函数为$f^*(y)=\sup_{x\in dom(f)}(y^Tx-f(x))$。

在x是实数的时候很容易理解

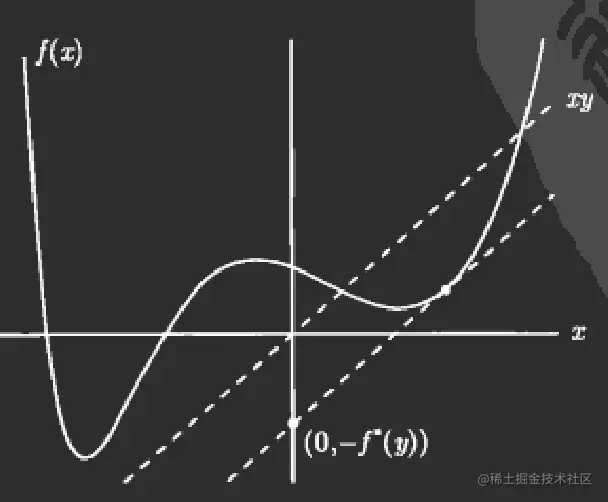
显然，共轭函数是凸函数，因为相当于有一系列关于$y$的函数，从里面找最大。而每一个关于y的函数都是y的凸函数。这和$f(x)$其实没有关系。

这个定义也要求了，y的取值必须保证上确界存在。比如对于一次函数$f(x)=ax+b$，那么很明显，其共轭函数$f^*(y)=\max_{x\in R}\{(y-a)x-b\}$，这个要想有界，y只能取$a$。

性质

• 1 Fenchel不等式：$f(x) + f^*(y)\ge x^T y$
• 2 $f$是凸函数且避函数（epigraph是闭的）, $f^{**}=f$
• 3 变换$g(x)=af(x)+b$，则$g^*(y)=af^*(y/a)-b$
• 4 变换$g(x)=f(Ax+b)$A是可逆方阵，$g^*(y)=f^*(A^{-T}y)-b^TA^{-T}y$
• 5 $g(u,v)=f_1(x)+f_2(y)$，那么$g^*(w,z)=f_1^*(w)+f_2^*(z)$

拟凸函数

比凸函数更弱的函数，可以不凸，但是凹的程度没那么大。

定义

定义域内的所有下水平集都是凸集。如果上水平集都是凸集，那么是拟凹函数。（比如logx，同时是拟凸和拟凹的）

比如实属函数的一个拟凸函数如下图

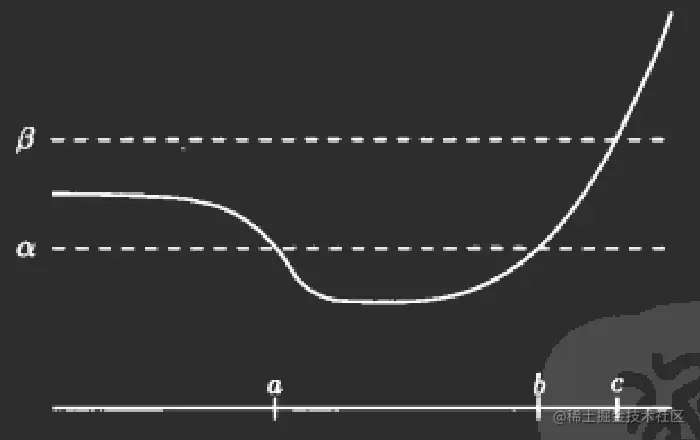
如果这个函数凹的程度再厉害一点，那么下水平集就可能是两段区间，这样就不是凸集了。

性质

• $f(\theta x + (1-\theta) y)\le \max\{f(x), f(y)\}$
• R上的连续函数，要么非增、要么非减、要么存在一个点$c$，左侧非增，右侧非减（单峰特性）
• 如果可微，那么拟凸的充要条件是定义域凸且$\forall x,y: f(y)\le f(x)\Rightarrow \nabla f(x)^T(y-x)\le 0$

相当于定义了下水平集的一个支撑超平面

• 如果二次可微，$y^T\nabla f(x)=0\Rightarrow y^T \nabla^2 f(x)y\ge 0$

R上的函数更直观，即一阶导为0的点，二阶导非负。

保拟凸运算

• 一系列拟凸函数的非负加权后，求最大
• 拟凸函数的复合函数是拟凸的
• $f(x,y)$是联合拟凸函数，C是凸集，那么$g(x)=\inf_{y\in C} f(x,y)$是拟凸函数。

转换表示

对于拟凸函数的下水平集，可以用一个凸函数的0不等式表示即

最naive的方法是indicator，在下水平集内取0，否则取1。因为拟凸函数保证了定义域是凸的，所以显然。但是不naive的需要结合函数特点来设计。

对数凸函数

• def：$\log f$是凸函数
• 性质$f(\theta x + (1-\theta)y)\ge f(x)^\theta f(y)^{1-\theta}$

凸优化问题

definition

$D$是公共定义域，$f$和$g$是凸函数，$h$是affine的，$h(x)=w^Tx+b$

相当于优化问题统一取最小化问题，限制条件可以是若干不等条件和等于条件，不等条件统一取小于等于。

凸最小化问题等价于一个凹最大化问题，都叫凸优化。
可以重新写成没有constraint的版本，就是目标中增加一个Indicator，在定义域内是0，否则无穷大。

性质

• 这类问题的好处是局部最优就是全局最优。
• 最优解集合为凸集
• f是严格凸那么解唯一
• 如果一阶可微，那么$x$是最优解等价于$\nabla f(x)(y-x)\ge 0$，相当于x处负梯度法向量的超平面构成对可行集的支撑。

问题变换

• partial optimization 可以把一个问题的决策变量，分别求最小，这是由于凸函数的保凸操作3保证的。因此可以先求一个变量的最小，再将其固定求另外一个。
• 目标转换 如果一个函数是单调增的，那么套一个重新求最小化，或者把原有的单调增函数去掉。这些变换可以应用于优化目标和constraint
• 变量映射 一一映射并且像包含可行域，那么$\min_x f(x), x\in C$等价于$\min_y f(\phi(y)), \phi(y)\in C$

比如几何优化就是非凸的
所谓几何优化是指优化目标和constraint都是posynomials的（$\sum_{i=1}^p \gamma_k x_1^{\alpha_1}x_2^{\alpha_2}...x_n^{\alpha_n}$这种形式），$\gamma>0$，$g_i(x)\le 1, h_i(x)=1$。
但是如果令$y_i=\log x_i, \gamma=e^b$，那$x_i=e^{y_i}$,带回原式可得$f(x)= e^{a^Ty+b}$，这就是凸了。

• 去除不等约束 对于$g_i(x)\le 0$，引入$s_i \ge 0$，且$g_i(x)+s_i=0$，注意只有$g_i$affine的时候才是convex的。
• 增加等式约束 把原来的变量，配凑成一个新的形式$z=\phi(x)$成为等式约束，然后把原始公式里配凑出来的$\phi(x)$变成z。
• 松弛等于约束 对于$g_i(x)=0$但$g_i$不是affine的情况，可以松弛为$g_i(x)\le 0$，这样可行域会变大，求完了还得验证分析。

拟凸优化

目标函数从凸函数变成了拟凸函数。这样传统的一阶最优充要条件$\nabla f(x)^T(y-x)\ge 0 \forall y$是不对的，但是我们有一个类似的充分条件:$\nabla f(x)^T (y-x)>0 \ \forall y\in X-\{x\}$

实际求解，可以利用其下水平集可以转化为凸函数的性质。即$f(x)\le t \Leftrightarrow \phi_t(x)\le 0$。所以可以求解如下凸优化问题：

二分搜索$t$，如果能找到$x$，搜索左侧，否则搜右侧。即，当我们能找到可行的x，意味着$f(x)\le t$可以进一步压缩（最小化f），等价于$\phi_t(x)\le 0$把t压缩。

四类典型问题

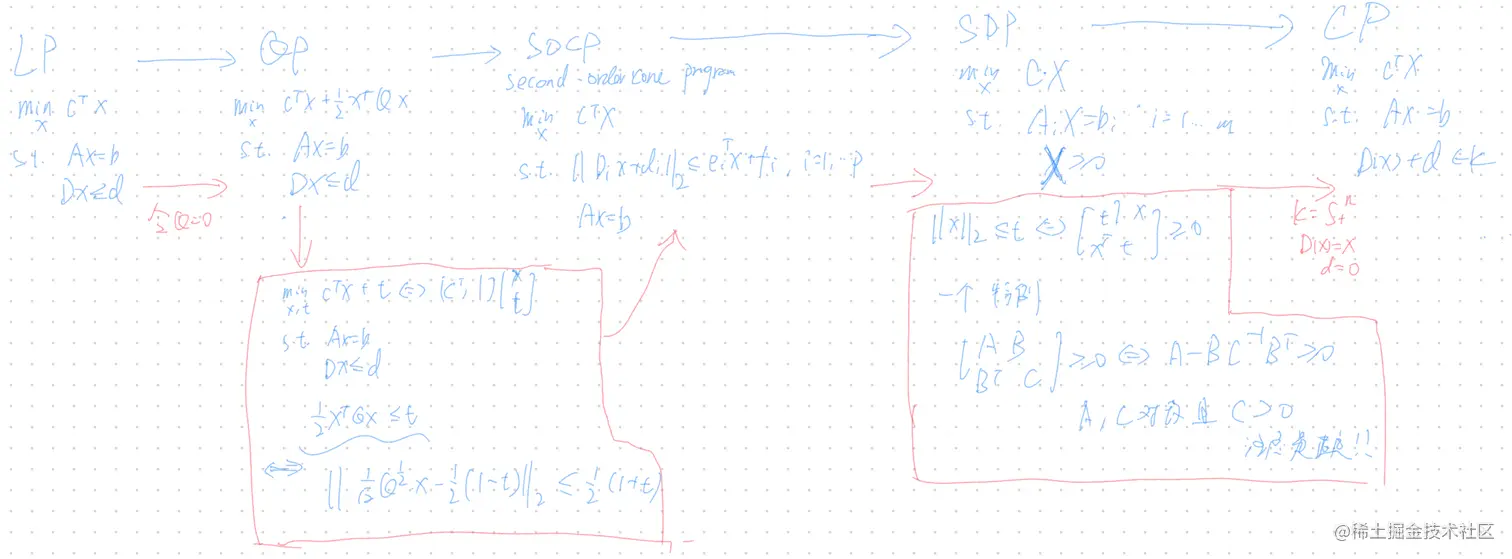
LP

案例：basis pursuit，如何应对绝对值？

转化为

LP问题的标准形式

变种：线性分式规划，即优化目标函数变成了$\frac{a^Tx+b}{c^Tx+d}$，要求分母大于0。

这个问题可以转化为线性规划，即另$y=\frac{x}{e^Tx+f}, z=\frac{1}{e^Tx+f}$，然后代换之前的x，优化y和z，优化完反向求出x。

QP

$Q$是半正定
标准形式

SDP

不等号定义半正定性$A\le B\equiv A-B$半正定，$F_i$是d阶对称方阵,$x_i$表示x向量的第i个元素。
标准形式

Conic Program

c、x是向量，A是矩阵，D把x线性映射到某一个欧氏空间$Y$，$d\in Y, K\subseteq Y$closed convex cone。

比如对于LP而言，$D(x)=x, d=0$，$K$是非负实数向量。

四类问题转换证明