5. 数组与广义表

5.1 数组的顺序存储

数组是由相同类型的数据元素构成的有限集合。

一维数组可以看作一个线性表，如图所示。

二维数组也可以看作一个线性表，只不过每一个数据元素也是一个线性表，如图所示。

于是，二维数组也可以看作一个线性表，只不过每一个数据元素也是一个线性表，如图所示。

数组一般采用顺序存储结构，因为存储单元是一维的，而数组可以是多维的，如何用一组连续的存储单元来存储多维数组呢？以二维数组为例，可以按行序存储，即先存第一行，再存第二行……也可以按列序存储，先存第一列，再存第二列……现在比较流行的C语言，Java都是按行序存储的。

1)按行序存储

如果按行序存储，怎么找到的存储位置呢？

先看看存储之前，前面已经存储了多少个元素，如图所示。

从图可以看出，在之前一共有i×n+j个元素，如果每个元素占用L字节，那么共需要(i×n+j)×L字节，只需要用基地址加上这些字节就可以得到的存储地址了。按行序存储，的存储地址为：

表示第一个元素的存储地址，即基地址，表示的存储地址。

2)按列序存储

如果按列序存储，怎么找到的存储位置呢？

先看看存储之前，前面已经存储了多少个元素，如图所示。

从图可以看出，在之前一共有j×m+i个元素，如果每个元素占用L字节，那么共需要(j×m+i)×L字节，只需要用基地址加上这些字节就可以得到的存储地址了。按列序存储，的存储地址为：

表示第一个元素的存储地址，即基地址，表示aij的存储地址。

注意：如果二维数组的下标是从1开始的，那么情形就变了。先看看存储之前，前面已经存储了多少个元素，如图所示。从图可以看出，行数和个数都少1，在aij之前一共有(i−1)×n+j−1个元素，如果每个元素占用L字节，那么共需要((i−1)×n+j−1)×L字节，只需要用基地址加上这些字节就可以得到的存储地址了。如果二维数组下标从1开始，按行序存储，的存储地址为：

存储地址计算秘籍：

的存储地址等于第一个元素的存储地址，加上前面的元素个数乘以每个元素占用的字节数。计算公式为：

5.2 特殊矩阵的压缩存储

在很多科学工程计算问题中，经常遇到一些特殊的矩阵，这些矩阵的很多值是相同的，有的很多元素是0，为了节省空间，可以对这类矩阵进行压缩存储。什么是压缩存储？给多个相同的元素分配一个存储空间，元素为0的不分配空间。什么样的矩阵能够压缩？一些特殊矩阵，如对称矩阵、三角矩阵、对角矩阵、稀疏矩阵等。什么叫稀疏矩阵？矩阵中非零元素的个数较少，怎样才算是较少呢？一般认为非零元素个数小于5%的矩阵为稀疏矩阵。

5.2.1 对称矩阵

对称矩阵比较特殊，其数据元素沿着对角线对称，即：
那么，因为上三角和下三角是一样的，因此只存储其中的一个就可以了。如果用一维数组存储下三角，则只需要n(n+1)/2个空间，比全部存储需要n^2个空间少了很多。

如果按行序存储下三角，那么怎么找到aij的存储位置呢？

先看看存储下三角中的之前，前面已经存储了多少个元素，如图所示。

如果将对称矩阵的下三角（i>= j）存储在一维数组s[ ]中，那么下三角中的下标就是i(i−1)/2+j−1，如图所示。

而上三角的元素（i<j），根据对称性，，可以直接读取下三角中的，因此按行序存储下三角时，的下标为：

存储下标计算秘籍：如果用一维数组s[ ]存储（下标从0开始），则的存储下标k等于前面的元素个数。

如果一维数组的下标从1开始呢？——公式后面再加1就行了。上面的公式是计算一维数组存储的下标，如果给了基地址（a11的存储地址），那么的存储地址为：

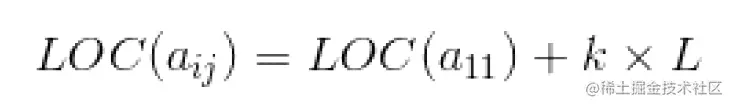
5.2.2 三角矩阵

三角矩阵比较特殊，分为下三角矩阵和上三角矩阵，下三角矩阵是指矩阵的下三角有数据，而其余的都是常数c或者为0，如图5-11所示。上三角矩阵也是如此，如图所示。

在下三角矩阵存储时，只需要存储其下三角中的元素，最后一个空间存储常数c即可。如果上面全为0，则不需要存储；下三角也是如此。

三角矩阵如果按行序存储，怎么找到的存储位置呢？

先看看存储之前，前面已经存储了多少个元素，如图所示。

如果一维数组的下标从零开始，那么下三角中的下标就是i(i−1)/2+j−1。而上三角的元素因为全是常数c或者为0，最后一个空间（下标为n(n+1)/2）存储常数c即可，如果是0，则不需要存储。因此下三角矩阵按行序存储时，的下标为：

上三角矩阵如果按行序存储，怎么找到aij的存储位置呢？

先看看存储之前，前面已经存储了多少个元素，如图所示。

如果一维数组的下标从0开始，那么上三角中的下标就是(i−1)(2n−i+2)/2+j−i。而下三角的元素全是常数c或者为0，最后一个空间（下标为n(n+1)/2）存储常数c即可。因此上三角矩阵按行序存储时，的下标为：

5.2.3 对角矩阵

对角矩阵又称为带状矩阵，是指在n×n的矩阵中非零元素集中在主对角线及其两侧，共L（奇数）条对角线的带状区域内，称为L对角矩阵，如图所示。

很明显，L对角矩阵的带宽为L，半带宽d=(L−1)/2。例如，5对角矩阵的半带宽d=2。当|i−j| d时，≠0，为对角矩阵的带状区域元素。当|i−j|>d时，=0，为对角矩阵的带状区域之外的元素。

1）L对角矩阵非零元素个数

L对角矩阵一共有多少个非零元素呢？

首先将每一行以对角线为中心进行补零，让每一行都达到L个元素，如图所示。一共补了多少个零呢？第一行补d个0，第二行补d−1个0左上角补零个数为d (d+1)/2。同理，右下角补零个数也为d(d+1)/2，总的补零个数为d(d+1)。那么每行按L个元素计算，再减去补零元素个数即可，即带状区域元素个数为L×n−d(d+1)。因为d=(L−1)/2，即L=2d+1，所以带状区域元素个数也可以表达为(2d+1)×n−d(d+1)。

2）按行序存储

补零后每行都有L个元素，需要L×n个空间。为了节省空间，第一行前面和最后一行后面的d个0可以不存储，“掐头去尾”，需要L×n−2d个空间。如图所示，阴影部分就是要存储的元素。

如果按行序，用一维数组s[]（下标从0开始）存储上图中的5对角矩阵，如下图所示。

怎么找到的存储位置呢？
首先找到的存储位置，因为是对角线上的元素，以对角线为中心，左右两侧都是d个元素，如图5-20所示。之前有i−1行，每行L个元素，所在行左侧有d个元素，因此之前有(i−1)×L+d个元素。因为第一行前面的d个0“掐头去尾”没有存储，所以之前有(i−1)×L个元素。的存储位置为：(i−1)×L。而和相差j−i个元素，也就说，的存储位置为：(i−1)×L+j−i。

在上图中，在的右侧（i<j），它们之间相差j−i个元素。如果在的左侧（i>j）呢？它们之间相差i−j个元素。只需要计算出的存储位置，减去它们之间的差值就可以了。即的存储位置为(i−1)×L−(i−j)=(i−1)×L+j−i。也就是说在的左侧或右侧，存储位置计算公式是一样的。
公式总结
按行序，用一维数组（下标从0开始）存储L对角矩阵，aij的存储位置为：
3对角矩阵中的存储位置为k=3(i−1)+j−i=2i+j−3。
5对角矩阵中的存储位置为k=5(i−1)+j−i=4i+j−5。
如果一维数组的下标从1开始，公式后面再加1即可。

3）按对角线存储

对角矩阵还有一种按对角线的顺序存储方式，如图所示。

即对角线作为0行，左侧分别为1, 2, …, d行，右侧分别为−1, −2, …, −d行。相当于行转换为i′=i−j，列值j不变，把n×n的L对角矩阵转换为L×n的矩阵，如图5-22所示。在图中，（a）矩阵中的对应（b）矩阵中的，其中。

在图（b）所示的矩阵中，将其他位置补零，如图5-23所示。用一维数组s[ ]（下标从0开始）按行序存储，仍然采用“掐头去尾”，第一行前面和最后一行后面的d个0不存储，如图5-24所示。

怎么找到的存储位置呢？

首先看n×n的L对角矩阵按对角线转换后的L×n的矩阵，如图5-25所示。之前有行，每行有n个元素，所在行左侧有j−1个元素，因此之前有个元素。因为第一行前面的d个0“掐头去尾”没有存储，所以之前有个元素。的存储位置为：。

如果用一维数组（下标从0开始）按行序存储，的下标为：
又因为，因此对角矩阵中的下标为：
公式总结
按对角线存储，对角矩阵中的下标为：

5.2.4 稀疏矩阵

稀疏矩阵是指非零元素个数较少，且分布没有规律可言，

那么少到什么程度才算稀疏呢？

一般认为非零元素小于5%时，属于稀疏矩阵。当然也没那么绝对，只要非零元素个数远远小于矩阵元素个数，就可以认为是稀疏矩阵，如图所示。

稀疏矩阵如何存储呢？

为了节省空间，只需要记录每个非零元素的行、列和数值即可，这就是三元组存储法，如图所示。

5.3 广义表

广义表是线性表的推广，也称为列表。它是个表元素组成的有限序列，记作。是表名，是表元素，它可以是表（称为子表），也可以是数据元素(称为原子)。为表的长度，的广义表为空表。

广义表最常见的操作就是求表头和表尾。
表头GetHead(L)：非空广义表的第一个元素，可以是一个单元素，也可以是一个子表。
表尾GetTail(L)：删除表头元素后余下的元素所构成的表。表尾一定是一个表。

例如，，表长为，表头为，表尾为，如图所示。

5.4 数组与广义表小结

虽然矩阵压缩有多种，但存储地址计算有一个通用公式。
存储地址计算秘籍：的存储地址等于第一个元素的存储地址，加上前面的元素个数乘以每个元素占用的字节数。计算公式为：

:表示第一个元素的存储地址，即基地址，表示的存储地址。
存储下标计算秘籍：如果用一维数组s[ ]存储（下标从0开始），则aij的存储下标k等于前面的元素个数。计算公式为：