顶刊TPAMI2022｜复旦大学研究团队提出基于贝叶斯理论的图像超分辨率网络BayeSR来自复旦大学医学影像、图像视觉与

论文标题：Bayesian Image Super-Resolution With Deep Modeling of Image Statistics
论文链接：ieeexplore.ieee.org/document/97…
代码仓库：github.com/shangqigao/…
作者单位：复旦大学

欢迎关注@CV顶刊顶会微信公众号，认真且严肃的计算机视觉论文前沿报道~

搜索框传播样式-标准色版.png

期刊介绍：IEEE Transactions on Pattern Analysis and Machine Intelligence（IEEE TPAMI）是计算机视觉和人工智能领域公认的顶级国际期刊，是中国计算机学会（CCF）推荐的A类期刊，其最新的影响因子为35.2。

对图像先验的统计信息进行建模对于图像超分辨率任务非常有用。来自复旦大学医学影像、图像视觉与人工智能实验室的研究团队提出了一个基于贝叶斯理论的图像超分辨率网络（Bayesian image super-resolution network，BayeSR），发表在人工智能领域顶级期刊IEEE Transactions on Pattern Analysis and Machine Intelligence（IEEE TPAMI）上。该框架结合平滑性和稀疏性先验对自然图像进行统计建模。具体来说，首先将理想图像视为平滑分量和稀疏残差的总和，并对包括模糊、缩小和噪声损坏在内的真实图像退化进行建模，并且设计了一种变分贝叶斯方法来推断它们的后验概率。最后作者结合深度神经网络实现了一个单图超分辨率（single image super-resolution (SISR)）变分网络，并且使用一种无监督学习策略进行训练。实验部分作者在三种图像恢复任务上进行实验，即理想的 SISR、现实的 SISR 和真实世界的 SISR，实验结果表明本文提出的方法对不同的噪声水平和退化等级具有良好的模型泛化能力。本文的代码和模型均已开源。

1.动机

目前用于解决SISR任务的方法大致可以分为基于建模的方法和基于学习的方法，前者将图像退化表示为分析或统计模型，其目的是在不使用任何进一步数据的情况下恢复退化的图像。这种设置下SISR被定义为一种不适定问题。因此，许多图像先验被提出来对自然图像的领域知识进行建模，例如高斯先验、马尔可夫随机场 (MRF)、稀疏性先验和低秩先验等等。但由于现实世界图像的复杂结构，单一的先验建模很难覆盖现实场景。因此，对图像结构进行建模仍然是具有挑战性的话题。而基于学习的方法旨在学习从退化空间到原始空间的映射。深度神经网络应用在 SISR 并取得了优于先前工作的性能。大多数在理想数据上训练的 SISR 模型，例如，通过双三次插值合成的模型，在图像包含噪声时不能很好地进行泛化。为了解决这个问题，可以在建模过程中明确地对图像先验建模，然后通过贝叶斯推理恢复它们。

此外，现有许多 SISR 模型是以监督的形式进行学习的，因此其很难用于没有Ground-Truth的真实场景中。为了解决这个问题，可以使用单个图像本身的信息进行内部学习，但由于其需要很多次梯度更新，这一类方法需要较长的推理时间。在本文中，作者旨在通过图像先验的显式建模来构建贝叶斯图像恢复框架。大多数基于学习的方法不对图像先验建模，通常使用均方误差（MSE）或平均绝对误差（MAE）进行判别学习，一旦输入图像中包含噪声，就可能导致模型泛化能力较差。本文提出研究两个图像先验，一个是平滑先验，另一个是稀疏先验。前者旨在对图像的局部相似分量进行建模，而引入后者是为了拟合图像的非平滑细节。由于任何图像都可以分解为分段平滑分量和更可能是稀疏的残差的总和[1]，因此可以构建一个深度网络来恢复 SISR 的平滑分量和稀疏残差。

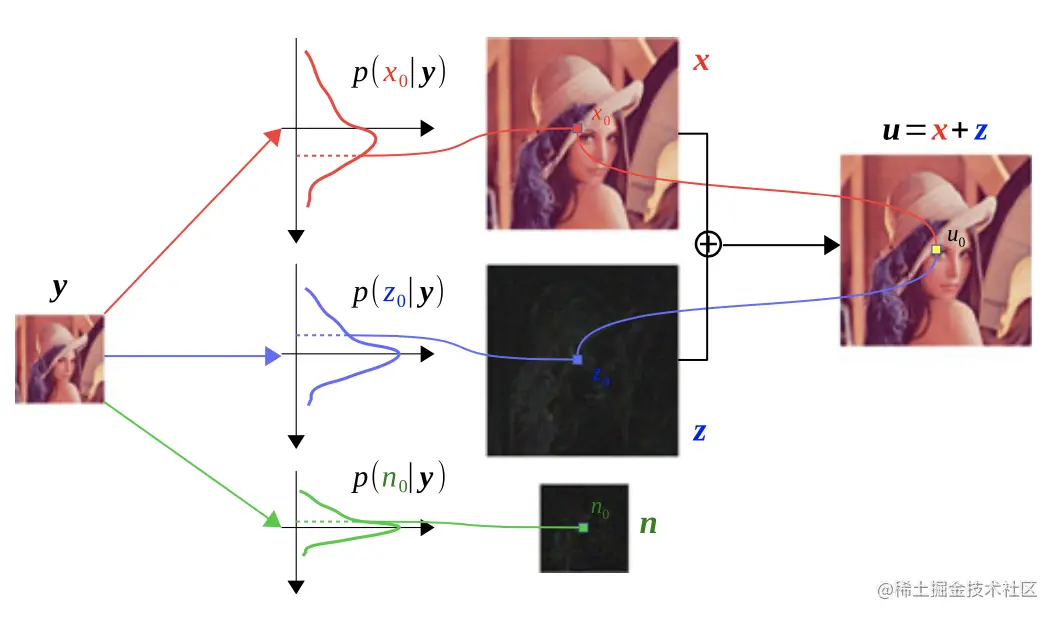
本文提出的贝叶斯图像超分辨率网络BayeSR，首先将每个图像建模为平滑分量和稀疏残差的总和。然后构建 DNN 来推断平滑度分量、稀疏残差和噪声的变分后验分布，即逐像素高斯分布，如下图所示。最后，我们对平滑度组合和稀疏残差进行采样，采集到的总和可以被认为是用来进行超分的信息，因此，BayeSR可以重复进行最后一步操作来为给定的退化图像生成很多超分版本，因此 BayeSR 是一种随机恢复方法，而不是确定性方法。

2.本文方法

2.1 图像退化建模

假设一张退化的图像是从某个变量 $\mathbf{y} \in \mathbb{R}^{d_{y}}$ 中采样得到的，其中 $d_{y}$ 表示 $y$ 的维度，而一幅清晰的图像是从 $\mathbf{u^{*}} \in \mathbb{R}^{d_{y}}$ 中采样得到，那图像的退化过程可以表示如下：

\mathbf{y}=\mathbf{A}(\mathbf{x}+\mathbf{z})+\mathbf{n}

其中， $\mathbf{x} \in \mathbb{R}^{d_{u}}$ 表示先验平滑度变量， $\mathbf{z} \in \mathbb{R}^{d_{u}}$ 表示稀疏先验变量， $\mathbf{n} \in \mathbb{R}^{d_{y}}$ 为高斯噪声。 $\mathbf{A}$ 表示含有卷积核 $\mathbf{k} \in \mathbb{R}^{d_{k}}$ 的下采样矩阵。

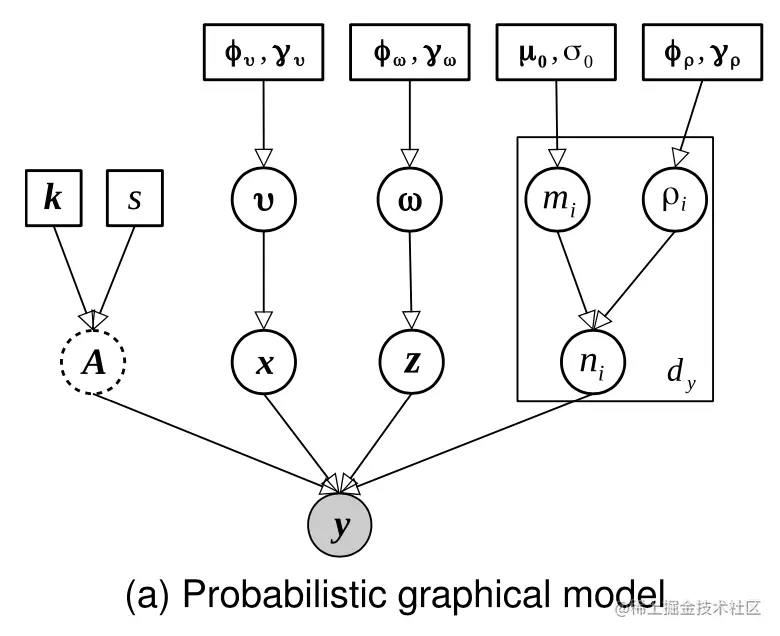
下图展示了使用概率图模型表示上述图像退化过程，其也被称为贝叶斯信念网络，对观察值 $\mathbf{y}$ 进行建模，具体而言， $\mathbf{y}$ 可以建模为平滑分量 $\mathbf{x}$ 、稀疏残差 $\mathbf{z}$ 、高斯噪声 $\mathbf{n}$ 和确定性下采样算子 $\mathbf{A}$ 的组合，其中 $\mathbf{x}$ 和 $\mathbf{z}$ 的总和被视为 $\mathbf{y}$ 的恢复信息。此外，高斯噪声 $\mathbf{n}$ 由均值 $\mathbf{m}$ 和方差决定，平滑分量 $\mathbf{x}$ 由空间相关性 $\nu$ 决定。稀疏残差 $\mathbf{z}$ 由稀疏精度 $\omega$ 决定。

2.2 后验分布的变分推理

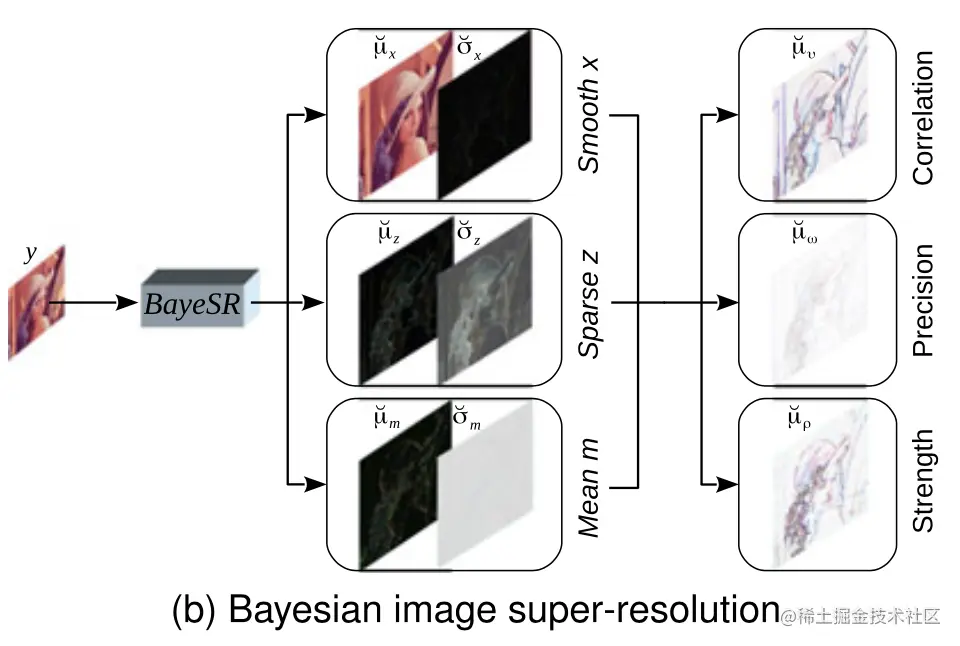
作者随后使用DNN来对 $\mathbf{x}$ ， $\mathbf{z}$ 和 $\mathbf{m}$ 的变分后验分布进行推断。如下图所示，变量集合为 $\boldsymbol{\psi}=\{\mathbf{m}, \boldsymbol{\rho}, \mathbf{x}, \boldsymbol{v}, \mathbf{z}, \omega\}$ 。

作者使用变分贝叶斯 (variational Bayesian，VB)进行推理，VB 方法通过变分后验分布 $q(\boldsymbol{\psi})$ 来逼近 $p(\boldsymbol{\psi} \mid \mathbf{y})$ 。最直接获得变分近似值的方法是最小化 $q(\boldsymbol{\psi})$ 和 $p(\boldsymbol{\psi} \mid \mathbf{y})$ 之间的 Kullback-Leibler (KL) 散度，如下所示：

\breve{q}(\boldsymbol{\psi}) \in \underset{q(\boldsymbol{\psi})}{\arg \min } \mathrm{KL}(q(\boldsymbol{\psi}) \| p(\boldsymbol{\psi} \mid \mathbf{y}))

因此所有变量 $\boldsymbol{\psi}=\{\mathbf{m}, \boldsymbol{\rho}, \mathbf{x}, \boldsymbol{v}, \mathbf{z}, \omega\}$ 的边缘分布的变分后验近似可以依次表示如下，

\begin{aligned} \breve{q}(\mathbf{m}) & =\mathcal{N}\left(\mathbf{m} \mid \breve{\boldsymbol{\mu}}_{m}, \operatorname{diag}\left(\breve{\boldsymbol{\sigma}}_{m}^{2}\right)\right) \\ \breve{q}(\boldsymbol{\rho}) & =\prod_{i=1}^{d_{y}} \mathcal{G}\left(\rho_{i} \mid \breve{\beta}_{\rho i}, \breve{\boldsymbol{\alpha}}_{\rho i}\right) \\ \breve{q}(\mathbf{x}) & =\mathcal{N}\left(\mathbf{x} \mid \breve{\boldsymbol{\mu}}_{x}, \operatorname{diag}\left(\breve{\boldsymbol{\sigma}}_{x}^{2}\right)\right) \\ \breve{q}(\boldsymbol{v}) & =\prod_{i=1}^{d_{u}} \mathcal{G}\left(v_{i} \mid \breve{\beta}_{v i}, \breve{\boldsymbol{\alpha}}_{v i}\right) \\ \breve{q}(\mathbf{z}) & =\mathcal{N}\left(\mathbf{z} \mid \breve{\boldsymbol{\mu}}_{z}, \operatorname{diag}\left(\breve{\boldsymbol{\sigma}}_{z}^{2}\right)\right) \\ \breve{q}(\boldsymbol{\omega}) & =\prod_{i=1}^{d_{u}} \mathcal{G}\left(\omega_{i} \mid \breve{\beta}_{\omega i}, \breve{\boldsymbol{\alpha}}_{\omega i}\right) \end{aligned}

在具体操作时，作者并没有直接计算 KL 散度，而是将其转换为如下更易于推导的公式，

\begin{aligned} \operatorname{KL}(\breve{q}(\boldsymbol{\psi}) \| p(\boldsymbol{\psi} \mid \mathbf{y})) & =\mathbb{E}[\log \breve{q}(\boldsymbol{\psi})]-\mathbb{E}[\log p(\boldsymbol{\psi} \mid \mathbf{y})] \\ & =\mathbb{E}[\log \breve{q}(\boldsymbol{\psi})]-\mathbb{E}[\log p(\boldsymbol{\psi}, \mathbf{y})]+\log p(\mathbf{y}) \end{aligned}

其中，由于所有期望都需要观察 $\breve{q}(\boldsymbol{\psi})$ ，而证据 $p(\mathbf{y})$ 仅取决于先验，该公式表明，最小化 KL 散度可以转化为：

\begin{aligned} & \min _{\breve{q}(\boldsymbol{\psi})} \mathbb{E}[\log \breve{q}(\boldsymbol{\psi})]-\mathbb{E}[\log p(\boldsymbol{\psi}, \mathbf{y})] \\ = & \min _{\breve{q}(\boldsymbol{\psi})} \mathrm{KL}(\breve{q}(\boldsymbol{\psi}) \| p(\boldsymbol{\psi}))-\mathbb{E}[\log p(\mathbf{y} \mid \boldsymbol{\psi})] \end{aligned}

基于此，模型的最终目标函数可以转化为：

\min _{\breve{q}(\boldsymbol{\psi})} \operatorname{KL}(\breve{q}(\boldsymbol{\psi}) \| p(\boldsymbol{\psi}))-\mathbb{E}_{\breve{q}(\boldsymbol{\rho})}[\log p(\mathbf{y} \mid \boldsymbol{\psi})]

随后作者对最终优化目标进行了理论解释，具体细节作者可参见原文。

2.3 BayeSR深度网络构建

由于迭代的 VB 算法需要对高维参数进行多次迭代，计算代价较大，因此作者选用DNN来构建BayeSR网络，DNN具有良好的非线性映射能力以及并行部署功能，更适合解决该问题。

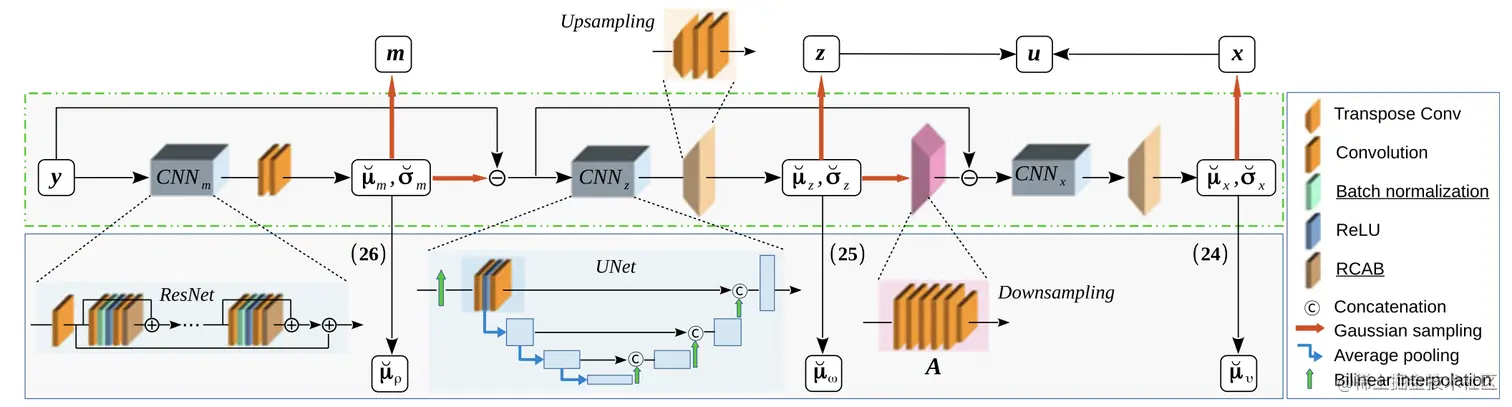
上图展示了BayeSR的整体框架，主要由三种类型的模块组成，即 CNN、上采样模块和下采样模块。CNN 模块可以使用 ResNet 或 UNet 的主干进行设计，CNN模块有三个，即 $CNN_{m}$ ， $CNN_{z}$ 和 $CNN_{x}$ ，分别用来估计 $\breve{q}(\boldsymbol{m})$ ， $\breve{q}(\boldsymbol{z})$ 和 $\breve{q}(\boldsymbol{x})$ 的分布参数。给定观察值 $\mathbf{y}$ ，首先使用 $CNN_{m}$ 估计出变量 $\mathbf{m}$ ，随后通过计算残差 $y-m$ ，并使用 $CNN_{z}$ 和上采样模块从残差中推断出稀疏残差 $\mathbf{z}$ 。最后，通过下采样模块对 z 进行下采样，该模块是为实现下采样算子 $\mathbf{A}$ 而开发的，并计算另一个残差 $\mathbf{y}-\mathbf{m}-\mathbf{Az}$ 。随后使用相同的方法来估计得到平滑分量 $\mathbf{x}$ 。

3.实验效果

在本文的实验部分，作者选用三个数据集对BayeSR进行训练，分别是DIV2K、Flickr2K 和 DPED，其中DIV2K1 首次发布于 SISR 上的 NTIRE 2017 挑战赛。Flickr2K 包含 2650 张不同的高分辨率图像。DPED3 由三部智能手机和一台专业相机在野外同步拍摄的照片组成。对于理想的 SISR，使用双三次 DIV2K，其中的退化图像是通过双三次插值合成的。对于真实的 SISR，使用温和的 DIV2K，其中退化图像被未知的泊松噪声和随机偏移破坏。对于现实世界的 SISR，采用DPED-iPhone，其中的退化图像被真实噪声破坏了。评价指标选用五个全参考图像质量评估指标，即 HR 空间峰值信噪比 (PSNR)、结构相似性 (SSIM) 指数、 LR 空间中的 PSNR (LRPSNR)、学习感知图像块相似度 (LPIPS) 和多样性 (Div.) 分数，以及两个无参考指标，即自然图像质量评估 (NIQE) 和空间质量评估 (BRISQUE)。

下表中展示了在理想SISR任务上的对比效果。

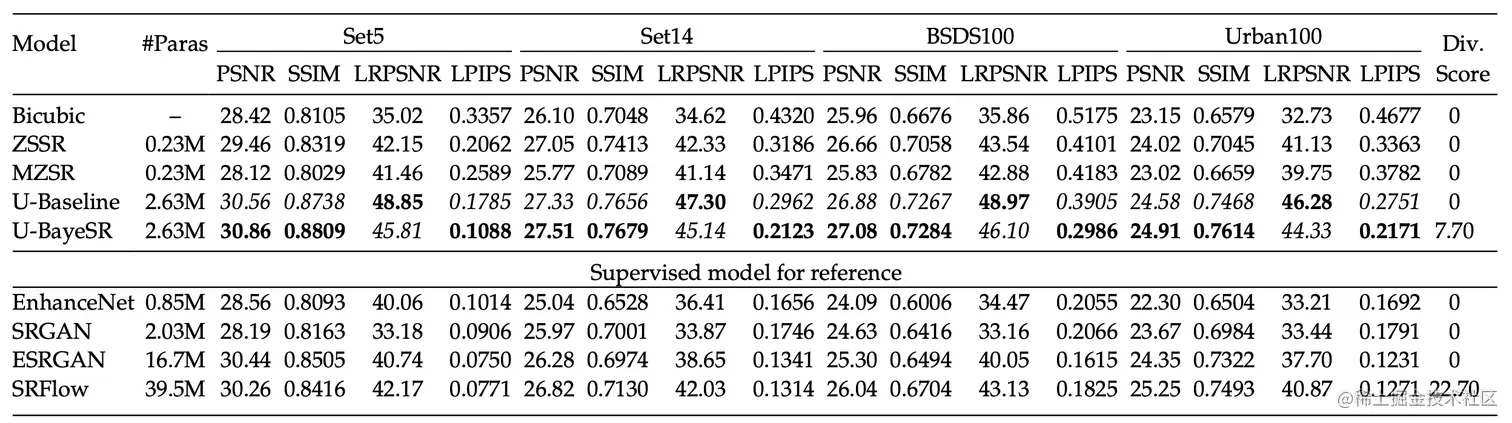
下图展示了BayeSR与其他方法的超分视觉对比效果，可以发现，BayeSR 可以恢复比其他无监督模型更多的图像细节。此外，监督模型可能会产生一些图像伪影，而 BayeSR 由于图像先验的显式建模而保持更好的局部相似性。

4.总结

在本文中，作者提出了一个贝叶斯图像超分框架BayeSR，并结合深度神经网络进行实现。具体来说，BayeSR首先使用平滑度和稀疏度先验对图像统计进行建模，并提出了从观察中估计平滑度分量和稀疏度残差的变分推理框架。然后，我们构建了神经网络来实现具体的变量估计，并提出了无监督策略来训练网络。最后，作者进行了大量的实验证明了BayeSR在无监督 SISR 任务中的有效性。

参考

[1] S. Osher, M. Burger, D. Goldfarb, J. Xu, and W. Yin, “An iterative regularization method for total variation-based image restoration,” Multiscale Model. Simul., vol. 4, no. 2, pp. 460–489, 2005.