什么是彼得森图表?
图是一种数据结构,由两个部分定义。
- 一个节点或一个顶点。
- 边缘E或有序对是两个节点u,v之间的连接,由唯一的一对(u,v)标识。这对(u,v)是有序的,因为在有向图的情况下,(u,v)与(v,u)是不一样的。边缘可能有一个权重,或者在无权重图的情况下被设置为1。
彼得森图。
彼得森图
- 是一个有10个顶点和15条边的立方图。
- 是唯一的(3,5)-笼子图和唯一的(3,5)-摩尔图。
- 是参数为3的奇数图。这是Kneser图,其中两个顶点是相邻的,当且仅当相应的子集是不相交的。
- 也是线型图k5的一个补充。
- 是最小的无桥3规则图,没有边3着色
- 在有10个顶点的3-regular图形中,有2000个生成树,是最多的。
彼得森图中没有3周期或4周期。

彼得森图
构造
彼得森图是由Hemi-dodecahedron的顶点和边组成的,Hemi-dodecahedron是一个十二面体,其对面的点、线、面都被标识在一起。
广义的彼得森图
通过将正多边形的顶点与星形多边形的等效顶点相连而产生的立方体图形家族被称为广义彼得森图形。广义彼得森图用P(n,k)来表示。

P(7,1)
如果n=7 ,k=7/2=3 ,P(7,1); P(7,2); P(7,3)
彼得森图形的色度数。
如上图所示,该图并不完整。此外,它有一个奇数的边。因此, 它不是一个二方图。
由于该图有偶数个顶点,彼得森图的色度数为3。
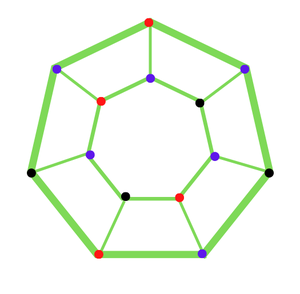
色度数=3
其他特征。
- 它是一个3连接的图,因此是3边连接和无桥的。
- 它有色度多项式t(t-1)(t-2)(t7-12t6+67t5-230t4+529t3-814t2+775t-352)
- 它是非平面的。
- 它不是 哈密顿式的。
- 彼得森图有一个哈密尔顿路径,但没有哈密尔顿循环。
例子。证明彼得森图形不是哈密顿式的。
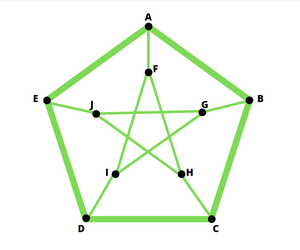
彼得森图
假设G是彼得森图,相反,假设G是哈密尔顿图。我们用数字A、B、C、D......J标记G的顶点,让T={AF、EJ、DI、CH、BG}为G的边的子集,那么G-T是断开的。因此,G的任何汉密尔顿循环必须包含T中的偶数边。不难看出,任何包含T中正好两条边的循环都不是汉密尔顿的。