如何利用矩阵实现平移、缩放、旋转等 3D 变换

羽月
2,944 阅读7分钟

上篇文章讲解了矩阵，利用矩阵我们可以轻松实现旋转、缩放等 3D 变换。另外在之前的一篇 CSS3 transform 和 canvas 背后不为人知的秘密 文章中详细讲解了平移、缩放、错切、旋转等 2D 变换，建议先看完这篇文章，这篇文章会基于这篇文章继续讲解 3D 变换不会从头再讲一遍。

组合变换和逆变换

在 CSS3 transform 和 canvas 背后不为人知的秘密 文章的最后介绍了这些 2D 变换如何用矩阵形式表示，可能有同学要问了，为啥非要用矩阵来表示这些变换，之前不挺好的吗？

这是因为用矩阵来实现，我们就可以利用矩阵的特性，实现非常强大的功能，比如我们可以将多个矩阵组合为一个单一矩阵，这个单一矩阵包含了所有的变换。

比如我们将一位置应用两个变换 A 和 B 矩阵。我们让 (B * A) 等于 C 矩阵。

newPosition = B * (A * position)
            = (B * A) * position
            = C * position

我们利用矩阵乘法可结合的性质，将 A 变换和 B 变换组合成了 C 变换。这样只用将位置乘上这个 C 矩阵就行了。我们可以拿这个 C 矩阵对其他点进行同样的变换了，而不需要每个点都重新计算下 B * A。

需要注意，我们首先是应用的 A 变换，然后再是 B 变换。但是由于我们使用的是列矢量，所以是 B * A * position，B 在 A 的前面。

例如，下面 A 是旋转变换，B 是平移变换。

C=B∗A=[10dx01dy001][cos(θ)−sin(θ)0sin(θ)cos(θ)0001]=[cos(θ)−sin(θ)dxsin(θ)cos(θ)dy001]\begin{aligned} C&=B*A \\ &=\begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ &=\begin{bmatrix} cos(\theta) & -sin(\theta) & dx \\ sin(\theta) & cos(\theta) & dy \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}

可以发现，C 矩阵是将旋转和平移组合起来，最右那一列是平移部分。也就是我们可以将一个矩阵变成线性变换部分和平移部分。

逆变换

使用矩阵的另一个好处是可以对一个变换做它的逆变换，用于撤销原始变换。比如向右旋转 90 度，那么它的逆变换就是向左旋转 90 度。

F−1(F(a))=F(F−1(a))=aF^{-1}(F(a)) = F(F^{-1}(a)) = a

对一个映射 FF 是可逆的需要存在一个逆运算 F−1F^{-1} ，满足上方式子。

我们可以发现上方介绍的变换都是可逆的，例如平移变换。

matrix=[10dx01dy001]matrix = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix}
invertMatrix=[10−dx01−dy001]invertMatrix = \begin{bmatrix} 1 & 0 & -dx \\ 0 & 1 & -dy \\ 0 & 0 & 1 \end{bmatrix}

将它平移部分变为负的即可。

绕中心旋转

我们还可以利用矩阵的特性推算出绕中心旋转矩阵。旋转一个物体时，一般希望绕它的中心旋转，而不是其他地方。要实现这个效果，我们可以对物体进行三次变换。

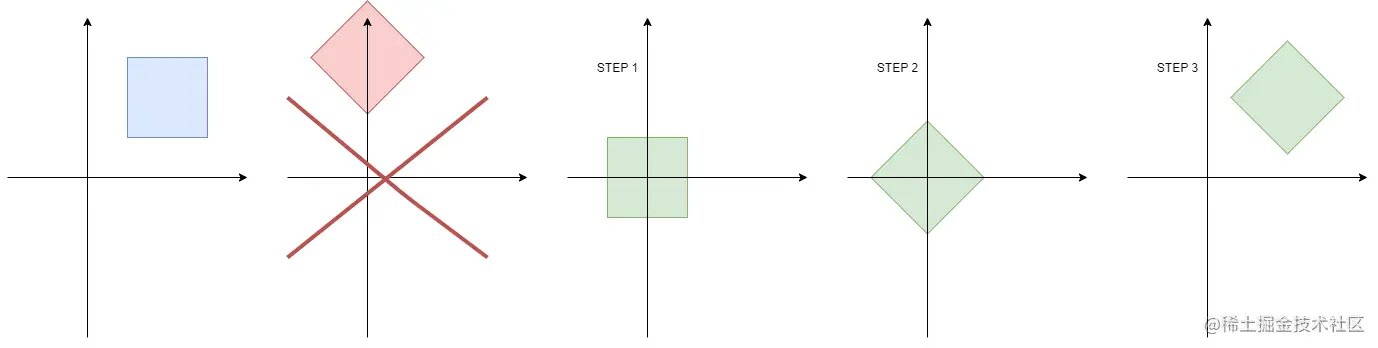
  1. 首先我们可以用平移矩阵 TT 将物体移动到原点。
  2. 再使用旋转矩阵 RR 旋转物体
  3. 最后使用第一次平移矩阵的逆矩阵 T−1T^{-1} 将物体移回原处
T=[10−dx01−dy001]T = \begin{bmatrix} 1 & 0 & -dx \\ 0 & 1 & -dy \\ 0 & 0 & 1 \end{bmatrix}
R=[cos(θ)−sin(θ)0sin(θ)cos(θ)0001]R = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix}
T−1=[10dx01dy001]T^{-1} = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix}

根据上方旋转和平移中得出的矩阵 T−1∗RT^{-1}*R 等于。

[cos(θ)−sin(θ)dxsin(θ)cos(θ)dy001]\begin{bmatrix} cos(\theta) & -sin(\theta) & dx \\ sin(\theta) & cos(\theta) & dy \\ 0 & 0 & 1 \end{bmatrix}

我们将这些矩阵组合起来。

M=T−1∗R∗T=[cos(θ)−sin(θ)−dx∗cos(θ)+dy∗sin(θ)+dxsin(θ)cos(θ)−dx∗sin(θ)−dy∗cos(θ)+dy001]\begin{aligned} M&=T^{-1}*R*T \\ &=\begin{bmatrix} cos(\theta) & -sin(\theta) & -dx * cos(\theta) + dy * sin(\theta) + dx \\ sin(\theta) & cos(\theta) & -dx * sin(\theta) -dy * cos(\theta)+dy \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}

这样我们就得到了一个绕中心旋转矩阵，任何图形应用这个矩阵都可以实现绕中心旋转。

3D 平移矩阵

3D 平移矩阵和 2D 一样，这里不做过多介绍

[100dx010dy001dz0001]\begin{bmatrix} 1 & 0 & 0 & dx \\ 0 & 1 & 0 & dy \\ 0 & 0 & 1 & dz \\ 0 & 0 & 0 & 1 \end{bmatrix}

缩放矩阵

3D 缩放矩阵也和 2D 的一样，这里也不做过多介绍。

[sx0000sy0000sz00001]\begin{bmatrix} sx & 0 & 0 & 0 \\ 0 & sy & 0 & 0 \\ 0 & 0 & sz & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

任意方向缩放

除了 X，Y，Z 轴方向，我们还可以实现任意方向缩放。假设我们任意方向是单位矢量 N。

上图中将矢量 VV ，沿着单位矢量 NN 进行缩放，缩放比例为 k，得到矢量 V′V' 。

将矢量 VV 分解为 V∥V\| 和 V⊥V\bot ，使得 V∥V\| 平行 NN ， V⊥V\bot 垂直于 V∥V\| ，并且 V=V∥+V⊥V=V\| + V\bot 。同样的将 V′V' 也分为 V′∥V'\| 和 V′⊥V'\bot 。

由于 V⊥V\bot 垂直 NN ，所以它不会受到缩放操作影响，对 VV 的缩放也就是对 V∥V\| 的缩放。

我们可以发现 V∥V\| 等于 (V⋅N)∗N(V \cdot N) * N，那么变换后 V′V' 就为。

V=V∥+V⊥V=V\| + V\bot
V∥=(V⋅N)∗NV\| = (V \cdot N) * N
V′⊥=V⊥=V−V∥=V−(V⋅N)∗N\begin{aligned} V'\bot &= V\bot \\ &= V-V\| \\ &= V-(V \cdot N) * N \end{aligned}
V′∥=kV∥=k∗(V⋅N)∗N\begin{aligned} V'\| &= kV\| \\ &= k * (V \cdot N) * N \end{aligned}
V′=V′⊥+V′∥=V−(V⋅N)∗N+k∗(V⋅N)∗N=V+(k−1)∗(V⋅N)∗N\begin{aligned} V' &= V'\bot + V'\| \\ &= V - (V \cdot N) * N + k * (V \cdot N) * N \\ &= V + (k - 1) * (V \cdot N) * N \end{aligned}

求出了 V′V' ，我们就可以得到在任意单位矢量 NN 方向，缩放 kk 的缩放矩阵。

[1+(k−1)Nx2(k−1)NxNy(k−1)NxNz0(k−1)NxNy1+(k−1)Ny2(k−1)NxNz0(k−1)NxNz(k−1)NyNz1+(k−1)Nz200001]\begin{bmatrix} 1+(k-1)N_x^2 & (k-1)N_xN_y & (k-1)N_xN_z & 0 \\ (k-1)N_xN_y & 1+(k-1)N_y^2 & (k-1)N_xN_z & 0 \\ (k-1)N_xN_z & (k-1)N_yN_z & 1+(k-1)N_z^2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

旋转矩阵

对于三维旋转，我们可以绕 X、Y 和 Z 轴旋转，每个旋转对应一个旋转矩阵。

我们还需要确认哪个方向是旋转正方向，我们这里用之前文章中提到的右手坐标系。

绕 X 轴旋转，X 轴坐标不变。

Rx=[10000cos(θ)−sin(θ)00sin(θ)cos(θ)00001]R_x = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) & 0 \\ 0 & sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

绕 Y 轴旋转，Y 轴坐标不变。

Ry=[cos(θ)0sin(θ)00100−sin(θ)0cos(θ)00001]R_y = \begin{bmatrix} cos(\theta) & 0 & sin(\theta) & 0 \\ 0 & 1 & 0 & 0 \\ -sin(\theta) & 0 & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

绕 Z 轴旋转，Z 轴坐标不变。

Rz=[cos(θ)−sin(θ)00sin(θ)cos(θ)0000100001]R_z = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & 0 \\ sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

我们可以看到 3D 旋转矩阵其实和 2D 差不多，另外旋转矩阵是正交矩阵，它的逆矩阵就等于它的转置矩阵（求矩阵的逆矩阵是性能开销比较大的运算，利用旋转矩阵的这个特性可以节省大量性能开销）。

根据上面公式我们可以写出公式对应的 JS 代码。

class Mat4 {
  static fromXRotation(rad) {
    const s = Math.sin(rad)
    const c = Math.cos(rad)
    return [
      1, 0, 0, 0,
      0, c, s, 0,
      0, -s, c, 0,
      0, 0, 0, 1
    ]
  }
  static fromYRotation(rad) {
    const s = Math.sin(rad)
    const c = Math.cos(rad)
    return [
      c, 0, -s, 0,
      0, 1, 0, 0,
      s, 0, c, 0,
      0, 0, 0, 1
    ]
  }
  static fromZRotation(rad) {
    const s = Math.sin(rad)
    const c = Math.cos(rad)
    return [
      c, s, 0, 0,
      -s, c, 0, 0,
      0, 0, 1, 0,
      0, 0, 0, 1
    ]
  }
}

在之前的 零基础玩转 WebGL - 着色器 文章的中我们利用 WebGL 渲染了一个立方体，但是看起来却像个正方形，这是因为它没有转起来，我们只能看得见它的正面所以看起来像个正方体。现在我们学会了旋转矩阵是时候让它旋转起来了。

code.juejin.cn/pen/7168479…

我们可以看到立方体旋转起来了，但是可能这个立方体看起来有一点点奇怪，这是因为还没有作透视处理，透视处理同样是利用矩阵来实现，透视将在下篇文章讲解。

绕任意过原点轴旋转

除了绕 X、Y、Z 轴，还可以绕任意轴旋转（该轴穿过原点，不考虑位移的情况）。假设绕任意轴单位矢量 N。

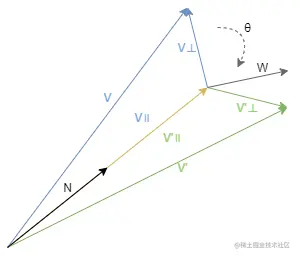
和任意方向缩放中一样，上图中 V′V' 是矢量 VV 沿单位矢量 NN 旋转 θ\theta 度后的结果。要求出 V′V' 的位置，我们可以将 VV 和 V′V' 拆分成垂直和平行分量，其中平行分量平行于 NN 。

我们可以发现旋转是应用在垂直分量上的，因为平行分量于旋转方向 NN 平行，不受旋转影响。我们现在可以把目标放在 2 维平面上的垂直矢量 V⊥V\bot 和 V′⊥V'\bot 。

我们可以构造一个 WW 矢量， WW 垂直 V⊥V\bot ，长度于 V⊥V\bot 相等。 WW 矢量等于 NN 叉乘 V⊥V\bot （叉乘在矢量中有讲）。

WW、 V⊥V\bot 、 V′⊥V'\bot 都在一个平面上，并且 WW 与 V⊥V\bot 垂直，我们把 WW 和 V⊥V\bot 当成水平和垂直坐标轴，根据上方讲到的二维旋转，我们可以得到。

V′⊥=cos(θ)∗V⊥+sin(θ)∗WV'\bot=cos(\theta)*V\bot + sin(\theta)*W

那么 V′V' 就等于。

V∥=(V⋅N)NV\| =(V \cdot N)N
V⊥=V−V∥=V−(V⋅N)N\begin{aligned} V\bot &= V-V\| \\ &=V-(V \cdot N)N \end{aligned}
W=N×V⊥=N×(V−V∥)=N×V−N×V∥=N×V\begin{aligned} W &= N \times V\bot \\ &=N \times (V - V\|) \\ &=N \times V - N \times V\| \\ &=N \times V \end{aligned}
V′=V′⊥+V′∥=cos(θ)∗V⊥+sin(θ)∗W+(V⋅N)∗N=cos(θ)∗(V−(V⋅N)∗N)+sin(θ)∗(N×V)+(V⋅N)∗N\begin{aligned} V' &= V'\bot + V'\| \\ &=cos(\theta) * V\bot + sin(\theta) * W + (V \cdot N) * N \\ &=cos(\theta) * (V - (V \cdot N) * N) + sin(\theta) * (N \times V) + (V \cdot N) * N \end{aligned}

把坐标轴基矢量带入上方式子中，那么绕任意过原点轴旋转的矩阵如下。

[Nx2(1−cos(θ))+cos(θ)NxNy(1−cos(θ))−Nzsin(θ)NxNz(1−cos(θ))+Nysin(θ)0NxNy(1−cos(θ))+Nzsin(θ)Ny2(1−cos(θ))+cos(θ)NyNz(1−cos(θ))−Nxsin(θ)0NxNz(1−cos(θ))−Nysin(θ)NyNz(1−cos(θ))+Nxsin(θ)Nz2(1−cos(θ))+cos(θ)00001]\begin{bmatrix} N_x^2(1-cos(\theta))+cos(\theta) & N_xN_y(1-cos(\theta))-N_zsin(\theta) & N_xN_z(1-cos(\theta))+N_ysin(\theta) & 0 \\ N_xN_y(1-cos(\theta))+N_zsin(\theta) & N_y^2(1-cos(\theta))+cos(\theta) & N_yN_z(1-cos(\theta))-N_xsin(\theta) & 0 \\ N_xN_z(1-cos(\theta))-N_ysin(\theta) & N_yN_z(1-cos(\theta))+N_xsin(\theta) & N_z^2(1-cos(\theta))+cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

总结

这篇文章如何利用矩阵变换物体，以及使用矩阵来变换物体和使用矩阵的好处。上面描述的各种变换中除了平移其他都是线性变换，任何线性变换都会将零矢量变换成零矢量，同时线性变换需要满足下方两个条件。

F(a+b)=F(a)+F(b)F(ka)=kF(a)F(a+b) = F(a) + F(b) \\ F(ka) = kF(a)

大家可以理解成线性变换不会使直线扭曲，变换后的平行线将继续平行。仿射变换是线性变换的超集，仿射变换包含平移。

这篇文章中渲染的立方体看起来有点奇怪，这是因为没有进行透视处理，下一篇文章将会讲解矩阵的另一个用处，如何实现相机功能。

如果觉得文章还不错欢迎点赞和关注来支持鼓励作者，我会尽快更新系列教程的下一篇文章。

零基础玩转 WebGL 系列文章目录请查看：零基础玩转 WebGL - 目录

avatar
文章
阅读
粉丝
相关推荐
高级前端应该掌握的数学知识-矩阵
4.1k阅读
 · 
65点赞
从零实现 3D 渲染引擎 - 相机矩阵
2.4k阅读
 · 
22点赞
用threejs实现火焰，超级简单
6.6k阅读
 · 
17点赞
如何实现物体透视效果 - 正交和透视投影矩阵
2.3k阅读
 · 
22点赞
THREE使用Curve曲线让小球沿着轨迹动起来
3.1k阅读
 · 
6点赞
Three.js实现穿越云层动效
4.2k阅读
 · 
36点赞
Three.js - 物体碰撞检测（二十六）
5.5k阅读
 · 
27点赞
第三篇：浅入一下 WebGL 的核心概念 - 着色器、坐标系统和纹理
283阅读
 · 
0点赞
THREE.JS实现地图+地球粒子效果之路
6.0k阅读
 · 
20点赞

友情链接：