看着所有非常大的卷积神经网络,如ResNets、VGG等,这就提出了一个问题:我们如何能用更少的参数使所有这些网络变得更小,同时还能保持同样的精度,甚至用更少的参数提高模型的泛化。一种方法是深度可分离卷积,在TensorFlow和Pytorch中也被称为可分离卷积(不要与空间可分离卷积混淆,后者也被称为可分离卷积)。深度可分离卷积是由Sifre在 "Rigid-motion scattering for image classification "中提出的,并且已经被流行的模型架构所采用,如MobileNet和Xception中的类似版本。它将通常在普通卷积层中结合在一起的通道和空间卷积分割开来
在本教程中,我们将研究什么是深度可分离卷积,以及我们如何使用它们来加速我们的卷积神经网络图像模型。
完成本教程后,你将学会
- 什么是纵深、点状和纵深可分离卷积
- 如何在Tensorflow中实现纵深可分离卷积
- 将它们作为我们计算机视觉模型的一部分
让我们开始吧!

概述
本教程分为三个部分
- 什么是深度可分离卷积
- 为什么它们有用?
- 在计算机视觉模型中使用纵深可分卷积
什么是纵深可分卷积?
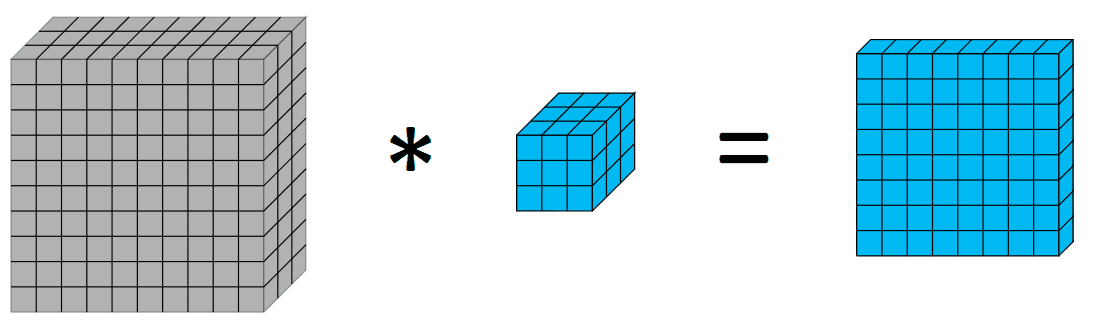
在深入研究深度可分卷积和深度可分卷积之前,快速回顾一下卷积可能会有所帮助。图像处理中的卷积是一个在体积上应用核的过程,我们对像素进行加权求和,其权重为核的值。视觉上,如下所示。
在10×10×3的图像上应用3×3的核,可以得到8×8×1的体积。
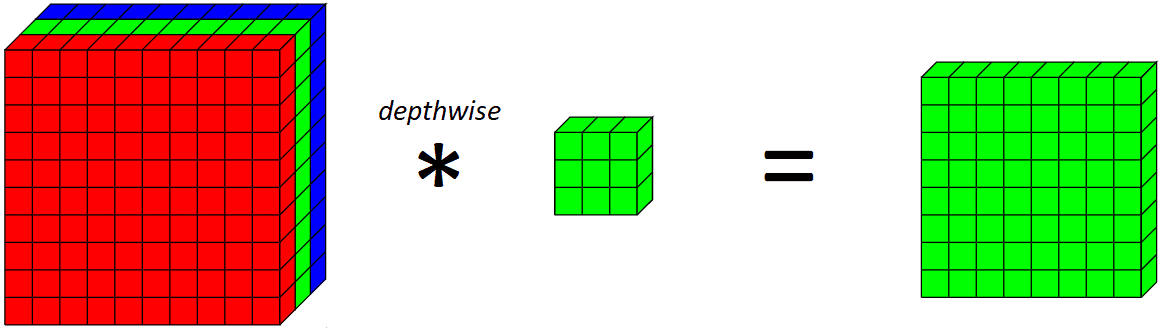
现在,我们来介绍一下深度卷积。深度卷积基本上是只沿着图像的一个空间维度进行卷积。在视觉上,这就是一个单一的深度卷积滤波器的样子和作用。
在这个例子中,在绿色通道上应用一个纵深3x3 核心
普通卷积层和深度卷积的关键区别在于,深度卷积只沿着一个空间维度(即通道)进行卷积,而普通卷积每一步都是在所有空间维度/通道上进行。
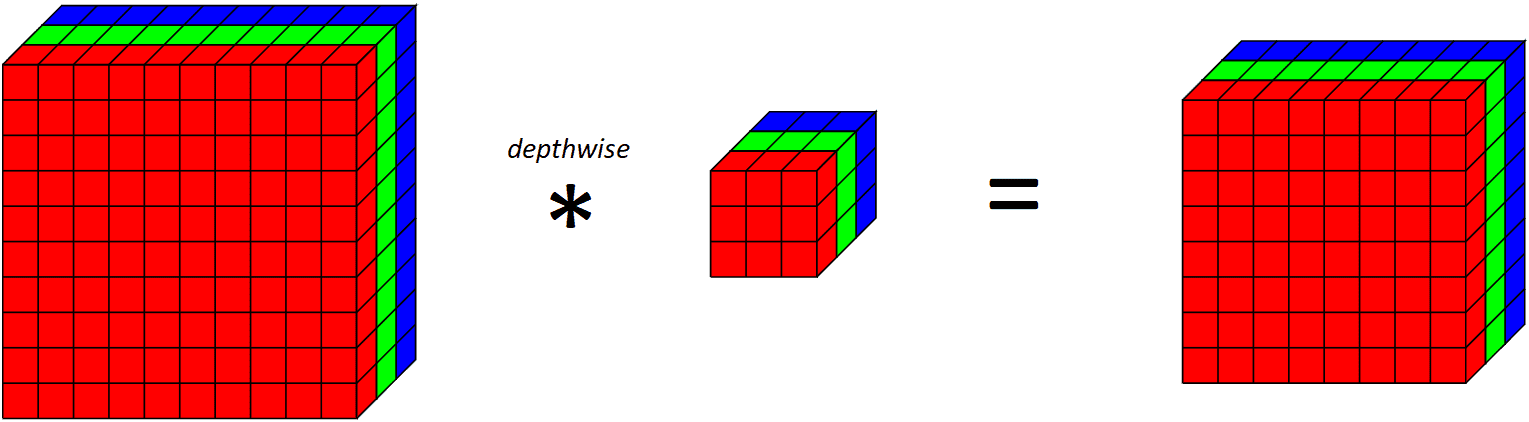
如果我们看一下整个深度卷积层对所有RGB通道的作用。
在10x10x3 输入体积上应用一个深度卷积滤波器,输出8x8x3 体积
注意,由于我们对每个输出通道应用一个卷积滤波器,输出通道的数量等于输入通道的数量。在应用这个深度卷积层后,我们再应用一个点卷积层。
简单地说,点式卷积层是一个带有1x1 核心的常规卷积层(因此在所有通道上看一个点)。在视觉上,它看起来像这样。
在一个10x10x3 的输入卷上应用点卷积,输出一个10x10x1 的输出卷。
为什么深度可分离卷积是有用的?
现在,你可能想知道,用纵深可分卷积做两个操作有什么用?鉴于本文的标题是为了加快计算机视觉模型的速度,那么做两次操作而不是一次操作对加快速度有什么帮助?
为了回答这个问题,让我们看看模型中的参数数量(虽然做两次卷积而不是一次会有一些额外的开销)。假设我们想对我们的RGB图像应用64个卷积滤波器,以便在我们的输出中拥有64个通道。普通卷积层的参数数(包括偏置项)为3次3次3次64+64=1792元。另一方面,使用深度可分离卷积层将只有参数,这是一个显著的减少,深度可分离卷积的参数不到正常卷积的6倍。
这可以帮助减少计算和参数的数量,从而减少训练/推理时间,并可以分别帮助我们的模型正规化。
让我们看看这个动作。对于我们的输入,让我们使用CIFAR10图像数据集的32x32x3 。
import tensorflow.keras as keras
from keras.datasets import mnist
# load dataset
(trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data()
然后,我们实现一个深度可分离卷积层。在Tensorflow中有一个实现,但我们将在最后的例子中进行讨论。
class DepthwiseSeparableConv2D(keras.layers.Layer):
def __init__(self, filters, kernel_size, padding, activation):
super(DepthwiseSeparableConv2D, self).__init__()
self.depthwise = DepthwiseConv2D(kernel_size = kernel_size, padding = padding, activation = activation)
self.pointwise = Conv2D(filters = filters, kernel_size = (1, 1), activation = activation)
def call(self, input_tensor):
x = self.depthwise(input_tensor)
return self.pointwise(x)
使用深度可分离卷积层构建一个模型,并查看参数的数量。
visible = Input(shape=(32, 32, 3))
depthwise_separable = DepthwiseSeparableConv2D(filters=64, kernel_size=(3,3), padding="valid", activation="relu")(visible)
depthwise_model = Model(inputs=visible, outputs=depthwise_separable)
depthwise_model.summary()
这就得到了输出
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_15 (InputLayer) [(None, 32, 32, 3)] 0
depthwise_separable_conv2d_ (None, 30, 30, 64) 286
11 (DepthwiseSeparableConv2
D)
=================================================================
Total params: 286
Trainable params: 286
Non-trainable params: 0
_________________________________________________________________
我们可以将其与一个使用普通二维卷积层的类似模型进行比较。
normal = Conv2D(filters=64, kernel_size=(3,3), padding=”valid”, activation=”relu”)(visible)
它给出的输出是
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input (InputLayer) [(None, 32, 32, 3)] 0
conv2d (Conv2D) (None, 30, 30, 64) 1792
=================================================================
Total params: 1,792
Trainable params: 1,792
Non-trainable params: 0
_________________________________________________________________
这与我们之前做的关于参数数量的初步计算相印证,并显示了使用深度可分离卷积可以实现参数数量的减少。
更具体地说,让我们看看普通卷积层和深度可分离卷积层中核的数量和大小。当看一个普通的二维卷积层,有通道作为输入,内核空间分辨率,通道作为输出,我们需要有参数,也就是过滤器,每个过滤器的内核大小为。然而,这对于类似的深度可分离卷积来说是不同的,即使有相同数量的输入通道、核空间分辨率和输出通道。首先是深度卷积,它涉及到滤波器,每个滤波器的核大小为,由于它作用于每个滤波器,所以输出通道。这个深度卷积层有参数(加上一些偏置单元)。然后是顺时针卷积层,它从深度卷积层吸收通道,并输出通道,因此我们有过滤器,每个过滤器的内核大小为。这个点卷积层有参数(加上一些偏置单元)。
你现在可能在想,但为什么他们能工作呢?
从Chollet的Xception论文中可以看出,一种思考方式是深度可分离卷积有一个假设,即我们可以分别映射跨通道和空间的相关性。鉴于此,卷积层中会有一堆冗余的权重,我们可以通过将卷积分离成深度和点度成分的两个卷积来减少这些权重。对于熟悉线性代数的人来说,一种思考方式是,当矩阵中的列向量是彼此的倍数时,我们如何能够将矩阵分解为两个向量的外积。
在计算机视觉模型中使用深度可分离卷积
现在我们已经看到了通过使用深度可分离卷积比普通卷积滤波器可以实现的参数减少,让我们看看如何在实践中使用Tensorflow的SeparableConv2D 滤波器。
在这个例子中,我们将使用上述例子中使用的CIFAR-10图像数据集,而对于模型,我们将使用一个基于VGG块建立的模型。深度可分离卷积的潜力在于更深的模型中,正则化效应对模型更有利,相对于LeNet-5这样的轻量级模型来说,参数的减少更明显。
使用VGG块创建我们的模型,使用普通卷积层。
from keras.models import Model
from keras.layers import Input, Conv2D, MaxPooling2D, Dense, Flatten, SeparableConv2D
import tensorflow as tf
# function for creating a vgg block
def vgg_block(layer_in, n_filters, n_conv):
# add convolutional layers
for _ in range(n_conv):
layer_in = Conv2D(filters = n_filters, kernel_size = (3,3), padding='same', activation="relu")(layer_in)
# add max pooling layer
layer_in = MaxPooling2D((2,2), strides=(2,2))(layer_in)
return layer_in
visible = Input(shape=(32, 32, 3))
layer = vgg_block(visible, 64, 2)
layer = vgg_block(layer, 128, 2)
layer = vgg_block(layer, 256, 2)
layer = Flatten()(layer)
layer = Dense(units=10, activation="softmax")(layer)
# create model
model = Model(inputs=visible, outputs=layer)
# summarize model
model.summary()
model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc")
history = model.fit(x=trainX, y=trainY, batch_size=128, epochs=10, validation_data=(testX, testY))
然后我们看一下这个6层卷积神经网络的正常卷积层的结果。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 32, 32, 3)] 0
conv2d (Conv2D) (None, 32, 32, 64) 1792
conv2d_1 (Conv2D) (None, 32, 32, 64) 36928
max_pooling2d (MaxPooling2D (None, 16, 16, 64) 0
)
conv2d_2 (Conv2D) (None, 16, 16, 128) 73856
conv2d_3 (Conv2D) (None, 16, 16, 128) 147584
max_pooling2d_1 (MaxPooling (None, 8, 8, 128) 0
2D)
conv2d_4 (Conv2D) (None, 8, 8, 256) 295168
conv2d_5 (Conv2D) (None, 8, 8, 256) 590080
max_pooling2d_2 (MaxPooling (None, 4, 4, 256) 0
2D)
flatten (Flatten) (None, 4096) 0
dense (Dense) (None, 10) 40970
=================================================================
Total params: 1,186,378
Trainable params: 1,186,378
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
391/391 [==============================] - 11s 27ms/step - loss: 1.7468 - acc: 0.4496 - val_loss: 1.3347 - val_acc: 0.5297
Epoch 2/10
391/391 [==============================] - 10s 26ms/step - loss: 1.0224 - acc: 0.6399 - val_loss: 0.9457 - val_acc: 0.6717
Epoch 3/10
391/391 [==============================] - 10s 26ms/step - loss: 0.7846 - acc: 0.7282 - val_loss: 0.8566 - val_acc: 0.7109
Epoch 4/10
391/391 [==============================] - 10s 26ms/step - loss: 0.6394 - acc: 0.7784 - val_loss: 0.8289 - val_acc: 0.7235
Epoch 5/10
391/391 [==============================] - 10s 26ms/step - loss: 0.5385 - acc: 0.8118 - val_loss: 0.7445 - val_acc: 0.7516
Epoch 6/10
391/391 [==============================] - 11s 27ms/step - loss: 0.4441 - acc: 0.8461 - val_loss: 0.7927 - val_acc: 0.7501
Epoch 7/10
391/391 [==============================] - 11s 27ms/step - loss: 0.3786 - acc: 0.8672 - val_loss: 0.8279 - val_acc: 0.7455
Epoch 8/10
391/391 [==============================] - 10s 26ms/step - loss: 0.3261 - acc: 0.8855 - val_loss: 0.8886 - val_acc: 0.7560
Epoch 9/10
391/391 [==============================] - 10s 27ms/step - loss: 0.2747 - acc: 0.9044 - val_loss: 1.0134 - val_acc: 0.7387
Epoch 10/10
391/391 [==============================] - 10s 26ms/step - loss: 0.2519 - acc: 0.9126 - val_loss: 0.9571 - val_acc: 0.7484
让我们试试同样的架构,但用Keras的SeparableConv2D 层代替普通卷积层。
# depthwise separable VGG block
def vgg_depthwise_block(layer_in, n_filters, n_conv):
# add convolutional layers
for _ in range(n_conv):
layer_in = SeparableConv2D(filters = n_filters, kernel_size = (3,3), padding='same', activation='relu')(layer_in)
# add max pooling layer
layer_in = MaxPooling2D((2,2), strides=(2,2))(layer_in)
return layer_in
visible = Input(shape=(32, 32, 3))
layer = vgg_depthwise_block(visible, 64, 2)
layer = vgg_depthwise_block(layer, 128, 2)
layer = vgg_depthwise_block(layer, 256, 2)
layer = Flatten()(layer)
layer = Dense(units=10, activation="softmax")(layer)
# create model
model = Model(inputs=visible, outputs=layer)
# summarize model
model.summary()
model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc")
history_dsconv = model.fit(x=trainX, y=trainY, batch_size=128, epochs=10, validation_data=(testX, testY))
运行上面的代码,我们就可以看到结果。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 32, 32, 3)] 0
separable_conv2d (Separab (None, 32, 32, 64) 283
leConv2D)
separable_conv2d_2 (Separab (None, 32, 32, 64) 4736
leConv2D)
max_pooling2d (MaxPoolin (None, 16, 16, 64) 0
g2D)
separable_conv2d_3 (Separab (None, 16, 16, 128) 8896
leConv2D)
separable_conv2d_4 (Separab (None, 16, 16, 128) 17664
leConv2D)
max_pooling2d_2 (MaxPoolin (None, 8, 8, 128) 0
g2D)
separable_conv2d_5 (Separa (None, 8, 8, 256) 34176
bleConv2D)
separable_conv2d_6 (Separa (None, 8, 8, 256) 68096
bleConv2D)
max_pooling2d_3 (MaxPoolin (None, 4, 4, 256) 0
g2D)
flatten (Flatten) (None, 4096) 0
dense (Dense) (None, 10) 40970
=================================================================
Total params: 174,821
Trainable params: 174,821
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
391/391 [==============================] - 10s 22ms/step - loss: 1.7578 - acc: 0.3534 - val_loss: 1.4138 - val_acc: 0.4918
Epoch 2/10
391/391 [==============================] - 8s 21ms/step - loss: 1.2712 - acc: 0.5452 - val_loss: 1.1618 - val_acc: 0.5861
Epoch 3/10
391/391 [==============================] - 8s 22ms/step - loss: 1.0560 - acc: 0.6286 - val_loss: 0.9950 - val_acc: 0.6501
Epoch 4/10
391/391 [==============================] - 8s 21ms/step - loss: 0.9175 - acc: 0.6800 - val_loss: 0.9327 - val_acc: 0.6721
Epoch 5/10
391/391 [==============================] - 9s 22ms/step - loss: 0.7939 - acc: 0.7227 - val_loss: 0.8348 - val_acc: 0.7056
Epoch 6/10
391/391 [==============================] - 8s 22ms/step - loss: 0.7120 - acc: 0.7515 - val_loss: 0.8228 - val_acc: 0.7153
Epoch 7/10
391/391 [==============================] - 8s 21ms/step - loss: 0.6346 - acc: 0.7772 - val_loss: 0.7444 - val_acc: 0.7415
Epoch 8/10
391/391 [==============================] - 8s 21ms/step - loss: 0.5534 - acc: 0.8061 - val_loss: 0.7417 - val_acc: 0.7537
Epoch 9/10
391/391 [==============================] - 8s 21ms/step - loss: 0.4865 - acc: 0.8301 - val_loss: 0.7348 - val_acc: 0.7582
Epoch 10/10
391/391 [==============================] - 8s 21ms/step - loss: 0.4321 - acc: 0.8485 - val_loss: 0.7968 - val_acc: 0.7458
请注意,在深度可分离卷积版本中,参数明显减少(约20万对约120万的参数),同时每个epoch的训练时间也略低。深度可分离卷积更有可能在可能面临过拟合问题的深层模型和具有较大内核的层上发挥更好的作用,因为参数和计算量的减少会抵消做两次卷积而不是一次卷积的额外计算成本。接下来,我们绘制了两个模型的训练和验证以及准确率,以查看模型训练性能的差异。
带有普通卷积层的网络的训练和验证准确率

带有深度可分离卷积层的网络的训练和验证准确率
两种模型的最高验证准确率相似,但纵深可分离卷积似乎对训练集的过拟合程度较低,这可能有助于它对新数据有更好的概括。
将所有的代码组合在一起,用于深度可分离卷积模型的版本。
import tensorflow.keras as keras
from keras.datasets import mnist
# load dataset
(trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data()
# depthwise separable VGG block
def vgg_depthwise_block(layer_in, n_filters, n_conv):
# add convolutional layers
for _ in range(n_conv):
layer_in = SeparableConv2D(filters = n_filters, kernel_size = (3,3), padding='same',activation='relu')(layer_in)
# add max pooling layer
layer_in = MaxPooling2D((2,2), strides=(2,2))(layer_in)
return layer_in
visible = Input(shape=(32, 32, 3))
layer = vgg_depthwise_block(visible, 64, 2)
layer = vgg_depthwise_block(layer, 128, 2)
layer = vgg_depthwise_block(layer, 256, 2)
layer = Flatten()(layer)
layer = Dense(units=10, activation="softmax")(layer)
# create model
model = Model(inputs=visible, outputs=layer)
# summarize model
model.summary()
model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc")
history_dsconv = model.fit(x=trainX, y=trainY, batch_size=128, epochs=10, validation_data=(testX, testY))
摘要
在这篇文章中,你已经看到了什么是纵深、点状和纵深可分离卷积。你还看到了使用纵深可分离卷积是如何让我们在使用明显较少的参数时获得有竞争力的结果。
具体来说,你已经学会了。
- 什么是纵深、点状和纵深可分离卷积?
- 如何在Tensorflow中实现纵深可分离卷积
- 将它们作为我们计算机视觉模型的一部分