持续创作,加速成长!这是我参与「掘金日新计划 · 1 月更文挑战」的第22天,点击查看活动详情
定义
在数学中某个序列的生成函数(母函数)是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。
使用母函数解决问题的方法称为母函数方法。
生成函数可分为很多种,如普通母函数、指数母函数、L级数、贝尔级数、狄利克雷级数等。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。
fib递推式
好像每一篇生成函数的博客都有这种东西
普通型生成函数
对于数列, 设, 则称G(x)是数列的生成函数。
一些公式
当时,
- (广义二项式定理)
举个栗子
第一个栗子
每一项都是1的无穷数列的生成函数是?
第二个栗子
设n∈N+,数列的生成函数是?
第三个栗子
小明有四个盒子,盒子里分别有1,2,3,4块蛋糕。
为了保证蛋糕的口感,一旦小明打开盒子就必须把盒子里的所有蛋糕都吃掉。
小明吃了若干块蛋糕。
(用生成函数求解以下问题)
(1)小明可能吃了几块蛋糕(显然以小明的胃口吃得下任意数量的蛋糕)?
(2)小明吃各种数量蛋糕打开盒子的方案分别是多少?
设生成函数G(x);
指数为蛋糕数,系数为方案数;
对于一个盒子,我们可以选择是否打开:
第一个盒子的方案:
第二个盒子的方案:
第三个盒子的方案:
第四个盒子的方案:
四个盒子的开合相互独立;最终方案
\begin{aligned} G(x)&=(x^0+x^1)\times(x^0+x^2)\times(x^0+x^3)\times(x^0+x^4) \&=x^0+x^1+x^2+2\times x^3\ &+2\times x^4+2\times x^5+2\times x^6+2\times x^7+x^8+x^9+x^{10} \end{aligned}
>我们可以从中得知,小明可能吃到0,1,2,3,4,5,6,7,8,8,10块蛋糕;
>
>有1种方案吃到0块,有1种方案吃到1块,有1种方案吃到2块,有2种方案吃到3块;
>
>有2种方案吃到4块,有2种方案吃到5块,有2种方案吃到6块,有2种方案吃到7块;
>
>有1种方案吃到8块,有1种方案吃到9块,有1种方案吃到10块。
### 第四个栗子
小明有四种盒子,每种盒子有无限个,盒子里分别有1,2,3,4块蛋糕。
为了保证蛋糕的口感,一旦小明打开盒子就必须把盒子里的所有蛋糕都吃掉。
小明吃了若干块蛋糕。
(1)小明可能吃了几块蛋糕(显然以小明的胃口吃得下任意数量的蛋糕)?
(2)小明吃各种数量蛋糕打开盒子的方案分别是多少?
(用生成函数求解)
>设生成函数G(x);
>
>指数为蛋糕数,系数为方案数;
>
>对于一个盒子,我们可以选择打开任意个或不打开:\
>第一个盒子的方案:$(x^0+x^1+x^2+x^3+...)$\
>第二个盒子的方案:$(x^0+x^2+x^4+x^6+...)$\
>第三个盒子的方案:$(x^0+x^3+x^6+x^9+...)$\
>第四个盒子的方案:$(x^0+x^4+x^8+x^{12}+...)$\
><br/>
>四个盒子的方案相互独立;\
>最终方案:
>$$
\begin{aligned}
G(x)&=(x^0+x^1+x^2+...)\times(x^0+x^2+x^4+...)\\
&\times(x^0+x^3+x^6+...)\times(x^0+x^4+x^8+...)
\end{aligned}
>$$
><br/>
>我们可以从中得知,小明可能吃了x(x∈N)块蛋糕;
>
>有1种方案吃到0块,有1种方案吃到1块,有2种方案吃到2块,有3种方案吃到3块;
>
>有5种方案吃到4块...
### 第五个栗子
小明有四种盒子,第一种盒子有无限个,每个装有两块蛋糕;第二种盒子有无限个,每个装有五块蛋糕;第三种盒子有四个,每个装有一块蛋糕,第四种盒子有一个,里面装有三块蛋糕。\
为了保证蛋糕的口感,一旦小明打开盒子就必须把盒子里的所有蛋糕都吃掉。\
小明吃了若干块蛋糕。\
(用生成函数求解)
(1)小明可能吃了几块蛋糕(显然以小明的胃口吃得下任意数量的蛋糕)?
(2)小明吃各种数量蛋糕打开盒子的方案分别是多少?
>设生成函数G(x);\
>指数为蛋糕数,系数为方案数;
><br/>
对于一个盒子,我们可以选择是否打开:\
第一个盒子的方案:$(x^0+x^2+x^4+x^6+...)$\
第二个盒子的方案:$(x^0+x^5+x^{10}+x^{15}+...)$\
第三个盒子的方案:$(x^0+x^1+x^2+x^3+x^4)$\
第四个盒子的方案:$(x^0+x^3)$
>
>四个盒子的方案相互独立;
>最终方案:
>$$
\begin{aligned}
>G(x)&=(x^0+x^2+x^4+x^6+...)\times (x^0+x^5+x^{10}+x^{15}+...)\\
&\times(x^0+x^1+x^2+x^3+x^4)\times(x^0+x^3)
\end{aligned}
>$$
# 指数型生成函数
数列{an}的指数型生成函数为$H(x)=\sum_{i=0}^\infty\frac{a_i*x^i}{i!}=\frac{a_1*x^0}{0!}+\frac{a_2*x^1}{1!}+\frac{a_3*x^2}{2!}+...$
## 一些公式
~~果然图片才是坠好的_(:3~~
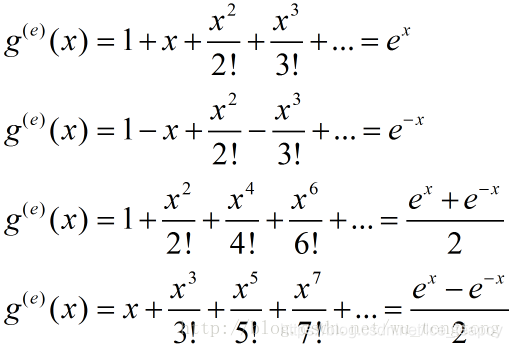
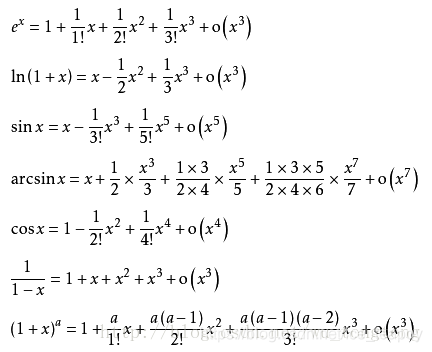
## 举个栗子
### 第一个栗子
小明有n个盒子,每个盒子可以容纳一块蛋糕;他有四种蛋糕,每种蛋糕有无限个。\
他要选择n块蛋糕装进盒子里。其中第一种蛋糕和第二种蛋糕必须打包偶数个。\
求不同的打包方案。\
(如果两种打包方案是不同的,那么必须存在至少一个盒子在两次打包中装有不同种类的蛋糕。)
>设指数型生成函数H(x),指数表示盒子数,系数表示方案数。\
><br/>
第一种蛋糕的方案:$(\frac{x^0}{0!}+\frac{x^2}{2!}+\frac{x^4}{4!}+...)$\
第二种蛋糕的方案:$(\frac{x^0}{0!}+\frac{x^2}{2!}+\frac{x^4}{4!}+...)$\
第三种蛋糕的方案:$(\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+...)$\
第四种蛋糕的方案:$(\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+...)$\
><br/>
四种蛋糕的方案相互独立;\
最终方案:\
$H(x)=(\frac{x^0}{0!}+\frac{x^2}{2!}+\frac{x^4}{4!}+...)^2\times (\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+...)^2$\
   $=(\frac{e^x+e^{-x}}{2})^2\times e^{2x}$\
   $=\frac{e^{4x}+2e^{2x}+1}{4}$\
   $=\frac14+\sum_{i=0}^{\infty}\frac{4^n+2^{n+1}}4\times \frac{x^n}{n!}$
>
>
>与普通生成函数相似,给n个盒子装入蛋糕的方案数为函数H(x)指数为n的项的系数$\frac{4^n+2^{n+1}}4$。
### 第二个栗子
被我吃掉了。
# 生成函数的运算
- F+G意义为可能是两种情况中的一种
- FG意义为同时选择两种情况
- E^F意义为自我组合