"一听就会，一写就废"的二分法

已经分析了

• 左闭右闭 $[left,right]$ 区间模型： 重识二分法（上）
• 左闭右开 $[left,right)$ 区间模型： 重识二分法（中）

本文开始分析其余两种区间模型：左开右闭 $(left,right]$ 、左开右开 $(left,right)$

左开右闭的区间模型

左开右闭区间模型，即 $(left, right]$，我们依然按照“六步法”进行逐一分析。

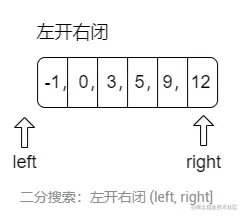
1、初始区间定义

区间初始值定义：$left = -1, right = len - 1$，其中 $len$ 是数组的长度。

2、循环条件选择

判断 $left==right$ 有意义么？举个例子，当 $left = right =2$ 时，落盘区间为 $(2,2]$，很明显该区间时没有意义的。故，循环条件为：$left \lt right$

3、mid指针讨论

当 $left$ 与 $right$ 之间的元素个数是偶数时：

举例说明：设 $nums$ 数组的长度为 $2n + 1$($n$ 正整数)。索引从 $0$ 到 $n-1$ 共 $n$ 个元素，索引从 $n+1$ 到 $2n$ 共 $n$ 个元素，所以索引为 $n$ 的元素恰为中间元素。初始情况下 $left = -1, right = 2n$， $left$ 与 $right$ 之间的元素个数为 $2n$（一定为偶数）。

👉使用 $mid = (left + right)/ 2$ 会使 $mid$ 指向中间偏左的元素。

此时 $mid$ 取值为：$mid = (-1 + 2n) / 2 = n - 1$（向下取整）

👉使用 $mid = (left + right + 1) / 2$ 会使 $mid$ 指向恰为中心的元素。

此时 $mid = (-1 + 2n + 1) / 2 = n$

👉使用 $mid = (left + right - 1) / 2$ 会使 $mid$ 指向中间偏左的元素。

此时 $mid = (-1 + 2n - 1) / 2 = n - 1$

当 $left$ 与 $right$ 之间的元素个数是奇数时：

举例说明：设 $nums$ 数组的长度为 $2n$ ($n$ 正整数)。索引从 $0$ 到 $n-2$ 共 $n-1$个元素，索引从 $n+1$ 到 $2n-1$ 共 $n-1$ 个元素，所以索引为 $n-1$（中间偏左） 与 $n$（中间偏右） 的元素为中间元素。初始情况下 $left = -1, right = 2n - 1$，$left$ 与 $right$ 之间的元素个数为 $2n-1$（一定为奇数）。

👉使用 $mid = (left + right) / 2$，会使 $mid$ 指向中间偏左的元素。

此时 $mid = (-1 + 2n -1) / 2 = n - 1$

👉使用 $mid = (left + right + 1) / 2$ ，会使 $mid$ 指向中间偏左的元素。

此时 $mid = (-1 + 2n - 1 + 1) / 2 = n - 1$（向下取整）

👉使用 $mid = (left + right - 1) / 2$ ，会使 $mid$ 指向过于偏左的元素（💥可能会丢失元素）。

此时 $mid = (-1 + 2n -1 - 1) / 2 = n - 2$（向下取整）

截止目前的讨论，对于 $(left, right]$ 区间模型，可先淘汰 $mid = (left + right - 1) / 2$（后面也会通过计算落盘新区间，证明该计算方法的不正确性），其他两种计算方法 $mid = (left + right) / 2$ 或 $mid = (left + right + 1) / 2$ 都可以满足条件，故还需要看计算出的落盘新区间，方可确定 $mid$ 的计算模型。

4、计算落盘新区间

通过比较 $nums[mid]$ 与 $target$，从而计算 $target$ 新的落盘区间，即

• $nums[mid] == target$，直接返回 $mid$ 即可；

• $nums[mid] > target$，说明 $target$ 一定在 $(left, mid)$ 区间内。我们发现，此区间模型已经违背了我们的“初心”，因此新的落盘区间应为 $(left, mid-1]$。故，此时应将右闭区间赋值给 $right$ 指针，即 $right = mid -1$；

• $nums[mid] < target$，说明 $target$ 一定在 $(mid, right]$ 区间内。我们发现，此区间模型与我们的“初心”一致。故，此时应将左开区间赋值给 $left$ 指针，即 $left = mid$。

💥注意啦！我们发现:

在每次计算落盘新区间时，如果 $nums[mid] > target$， $right$ 指针都会发生改变（每次循环后的 $right$ 会比前一次循环的少1）;如果 $nums[mid] < target$， $left$ 指针也不一定会发生变化（有可能当次计算出来的 $mid$ 与上一次的 $left$ 值相同）

💥 故我们猜想，在某种 $mid$ 指针的计算方法下，可能会出现“死循环”。

如采用 $mid = (left + right) / 2$ 亦或 $mid = (left + right - 1) / 2$，那么当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k+1$ 个元素，其中 $k \in [0, len-1)$，并且 $nums[mid] < target$ 时， $left$ 和 $mid$ 会反复指向最后第一个元素，进入死循环。

证明一下：当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k+1$ 个元素，

• 代入 $mid = (left + right) / 2$，可得：$mid = k + 1/2 = left$；

• 代入 $mid = (left + right - 1) / 2$，可得：$mid = k = left$。

而此时 $nums[mid] < target$，$mid$ 指针要赋值给 $left$指针，导致 $mid$ 和 $left$指针反复赋值，故一旦命中上述两种情况，二分法将陷入“死循环”中。

故只有 $mid = (left + right + 1) / 2$ 可以满足要求。故 $mid$ 计算方式为: $mid= left + (right - left + 1) \gt\gt 1$

证明一下：当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k + 1$ 个元素，

代入 $mid = (left + right + 1) / 2$，可得：$mid = k + 1 = right$；

• 此时如果 $nums[mid] == target$，直接返回 $mid$；

• 此时如果 $nums[mid] < target$，$mid$ 指针要赋值给 $left$ 指针，$left$ 和 $right$ 均指向第 $k + 1$ 个元素，循环退出（因为循环执行条件是 $left < right$），返回 $-1$；

• 此时如果 $nums[mid] > target$，$mid - 1$ 赋值给 $right$ 指针，此时$left$ 和 $right$ 均指向第 $k$ 个元素，循环退出，返回 $-1$;

5、最终返回值

如果 $target$ 的确存在于 $nums$ 数组中，一定会在第四步中 $nums[mid] == target$ 时返回，否则返回 $-1$ 即可。

6、代码参考

迭代法

/**
 * 区间模型 (left, right]
 * 空间复杂度 o(1)
 * 时间复杂度 o(logN)
 */
function search(nums: number[], target: number): number {
	let left = -1;
	let right = nums.length - 1;
	
	while(left < right) {
		const mid = left + ~~((right - left + 1) / 2); // 只有一种 mid 模型
		const midVal = nums[mid];
		
		if (midVal === target) {
			return mid;
		}
		
		if (midVal > target) {
			right = mid - 1;
		} else  {
			left = mid;
		}
	}
	
	return -1;
}

递归法

/**
 * 区间模型 (left, right]
 * 空间复杂度 o(logN)
 * 时间复杂度 o(logN)
 */
 function search(nums: number[], target: number): number {
     return searchHelper(nums, target, -1, nums.length - 1); 
 }
 
 function searchHelper(nums: number[], target: number, left: number, right: number ): number {
     if (left >= right) {
         return -1;
     }
     // [0, +infinity), 强行向下取整, 例如 ~~(1.5) == 1
     // (-infinity, 0), 强行向上取整, 例如 ~~(-0.5) == 0, ~~(-1.5) == -1
     
     const mid = left + ~~((right - left + 1) / 2); // 仅一种方式
     if (nums[mid] === target) {
         return mid;
     }
     
     if (nums[mid] > target) {
         return searchHelper(nums, target, left, mid - 1);
     }
     
     return searchHelper(nums, target, mid, right);
 }

左开右开的区间模型（无解）

左开右开区间模型，即 $(left,right)$，我们依然按照“六步法”进行逐一分析。

1、初始区间定义

区间初始值定义：$left = -1, right = len$，其中 $len$ 是数组的长度。

2、循环条件选择

判断 $left == right$ 有意义么？举个例子，当 $left = right =2$ 时，落盘区间为 $(2,2)$，很明显该区间是没有意义的。故，$left \lt right$

3、mid指针讨论

当 $left$ 与 $right$ 之间的元素个数是偶数时：

举例说明：$nums$ 数组的长度为 $2n$ ($n$ 是正整数)。索引从 $0$ 到 $n-2$ 共 $n-1$ 个元素，索引从 $n+1$ 到 $2n-1$ 共 $n-1$ 个元素，所以索引为 $n-1$（中间偏左） 或 $n$（中间偏右） 的元素即为中间元素。初始情况下 $left = -1, right = 2n$，$left$ 与 $right$ 之间的元素个数为 $2n$（一定为偶数）。

👉使用 $mid = (left + right) / 2$ 会使 $mid$ 指向中间偏左的元素。

此时 $mid = (-1 + 2n) / 2 = n - 1$（向下取整）

👉使用 $mid = (left + right + 1) / 2$ 会使 $mid$ 指向中间偏右的元素。

此时 $mid = (-1 + 2n + 1) / 2 = n$

👉使用 $mid = (left + right - 1) / 2$ 会使 $mid$ 指向中间偏左的元素。

此时 $mid = (-1 + 2n - 1) / 2 = n -1$

当 $left$ 与 $right$ 之间的元素个数是奇数时：

举例说明： $nums$ 数组的长度为 $2n + 1$ ($n$ 正整数)。索引从 $0$ 到 $n-1$ 共 $n$ 个元素，索引从 $n+1$ 到 $2n$ 共 $n$ 个元素，所以索引为 $n$ 的元素恰为中间元素。初始情况下 $left = -1, right = 2n + 1$， $left$ 与 $rgiht$ 之间的元素个数为 $2n + 1$（一定为奇数）。

👉使用 $mid = (left + right) / 2$，会使 $mid$ 指向恰为中心的元素。

此时 $mid = (-1 + 2n + 1) / 2 = n$

👉使用 $mid = (left + right + 1) / 2$，会使 $mid$ 指向恰为中心的元素。

此时 $mid = (-1 + 2n + 1 + 1) / 2 = n$

👉使用 $mid = (left + right - 1) / 2$ ，会使 $mid$ 指向中间偏左的元素。

此时 $mid = (-1 + 2n + 1 - 1) / 2 = n - 1$

截止目前的讨论，对于 $(left, right)$ 区间模型， $mid$ 三种计算模型都可以满足条件，故还需要讨论计算出的落盘新区间，方可确定 $mid$ 的计算模型。

4、计算落盘新模型

通过比较 $nums[mid]$ 与 $target$ ，从而计算 $target$ 新的落盘区间，即

• $nums[mid] == target$，直接返回 $mid$ 即可；

• $nums[mid] > target$，说明 $target$ 一定在 $(left, mid)$ 区间内。我们发现，此区间模型符合我们的“初心”，即 $(left, right)$。故，此时应将新的右开区间赋值给 $right$ 指针，即 $right = mid$；

• $nums[mid] < target$，说明 $target$ 一定在 $(mid, right)$ 区间内。我们发现，此区间模型与我们的“初心”一致。故，此时应将左开区间赋值给 $left$ 指针，即 $left = mid$。

💥注意啦！我们发现：

在每次计算落盘新区间时，即使 $nums[mid] > target$， $right$ 指针也不一定会发生变化（有可能当次计算出来的 $mid$ 与上一次的 $right$ 值相同）；即使 $nums[mid] < target$， $left$ 指针也不一定会发生变化（有可能当次计算出来的 $mid$ 与上一次的 $left$ 值相同）。

💥 故我们猜想，在某种 $mid$ 指针的计算方法下，可能会出现“死循环”。

先说结论：当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k+1$ 个元素，其中 $k \in [0, len-1)$，并且 $nums[mid] < target$ 时，在 $mid = (left + right) / 2$ 与 $left$ 和 $mid = (left + right - 1) / 2$ 计算方式下，$mid$ 会反复指向第一个元素，进入死循环。

证明一下：当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k+1$ 个元素，

• 代入 $mid = (left + right) / 2$ 可得：$mid = (left + left + 1) / 2 = left + 1/2 = left$；

• 代入 $mid = (left + right - 1) / 2$ 可得：$mid = (left + left + 1 - 1) / 2 = left$。

而此时 $nums[mid] < target$，$mid$ 指针要赋值给 $left$ 指针，导致 $mid$ 和 $left$ 指针反复赋值，故一旦命中上述两种情况，二分法将陷入“死循环”中。

先说结论：当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k+1$ 个元素，其中 $k \in [0, len-1)$，并且 $nums[mid] > target$ 时，在$mid = (left + right + 1) / 2$ 计算方式下，$right$ 和 $mid$ 会反复指向第二个元素，进入死循环。

证明一下：当 $left$ 指向第 $k$ 个元素，而 $right$ 指向第 $k+1$ 个元素，

• 代入 $mid = (left + right + 1) / 2$ 可得：$mid = (right + right) / 2 = right$。

而此时 $nums[mid] > target$，$mid$ 指针要赋值给 $right$ 指针，导致 $mid$ 和 $right$ 指针反复赋值，故一旦命中上述两种情况，二分法将陷入“死循环”中。

故不管选择哪种计算方式，均不能满足要求（可以自行证明）。例如数组 $[-1,0,3,5,9,12]$ 中寻找值为 $2$ 的索引。

总结

重识二分法（上）、重识二分法（中）、重识二分法（下）证明了二分法四种区间模型 $[left, right]$、$[left, right)$、$(left, right]$、$(left, right)$ 的稳定性，以及其对应的循环条件以及 $mid$ 计算方式的有效性：

区间模型	循环条件	$mid$ 指针取值	指针交换
$[left, right]$	$left \le right$	$mid = (left + right)/2$ $mid = (left + right + 1) / 2$ $mid = (left + right - 1) / 2$	如果 $nums[mid] > target$, $right = mid - 1$ 否则 $left = mid + 1$
$[left, right)$	$left \lt right$	$mid = (left + right) / 2$ $mid = (left + right - 1) / 2$	如果 $nums[mid] > target$, $right = mid$ 否则 $left = mid + 1$
$(left, right]$	$left \lt right$	$mid = (left + right + 1) / 2$	如果 $nums[mid] > target$, $right = mid - 1$ 否则 $left = mid$
$(left, right)$	无解	无解	无解

对于二分搜索算法，最重要的三点：区间模型、循环条件、$mid$ 指针取值。熟记适合自己理解的组合，以不变应万变，方可举一反三。

参考

理论参考

二分查找的细节(左闭右闭、左闭右开、左开右闭)及其两段性

题目参考

35. 搜索插入位置