如何在Python中实现Logistic Sigmoid函数在本教程中，我将向你展示如何在Python中实现一个logi

在本教程中，我将向你展示如何在Python中实现一个logistic sigmoid函数。

我将解释什么是 logistic sigmoid 函数。

我将向你展示如何在 Python 中定义 logistic sigmoid 函数的语法。

我还会向你展示几个它是如何工作的例子。

如果你需要具体的东西，你可以点击以下任何一个链接。

Logistic Sigmoid函数简介
Python中Logistic Sigmoid的语法
如何使用Logistic Sigmoid函数的例子

让我们先简单介绍一下这个函数是什么。

Logistic Sigmoid函数的介绍

Logistic sigmoid函数是一个s型函数，其定义如下。

(1 ) 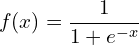$\begin{equation*} f(x) = \frac{1}{1 + e^{-x}} \end{equation*}$

当我们绘制它时，它看起来像这样。

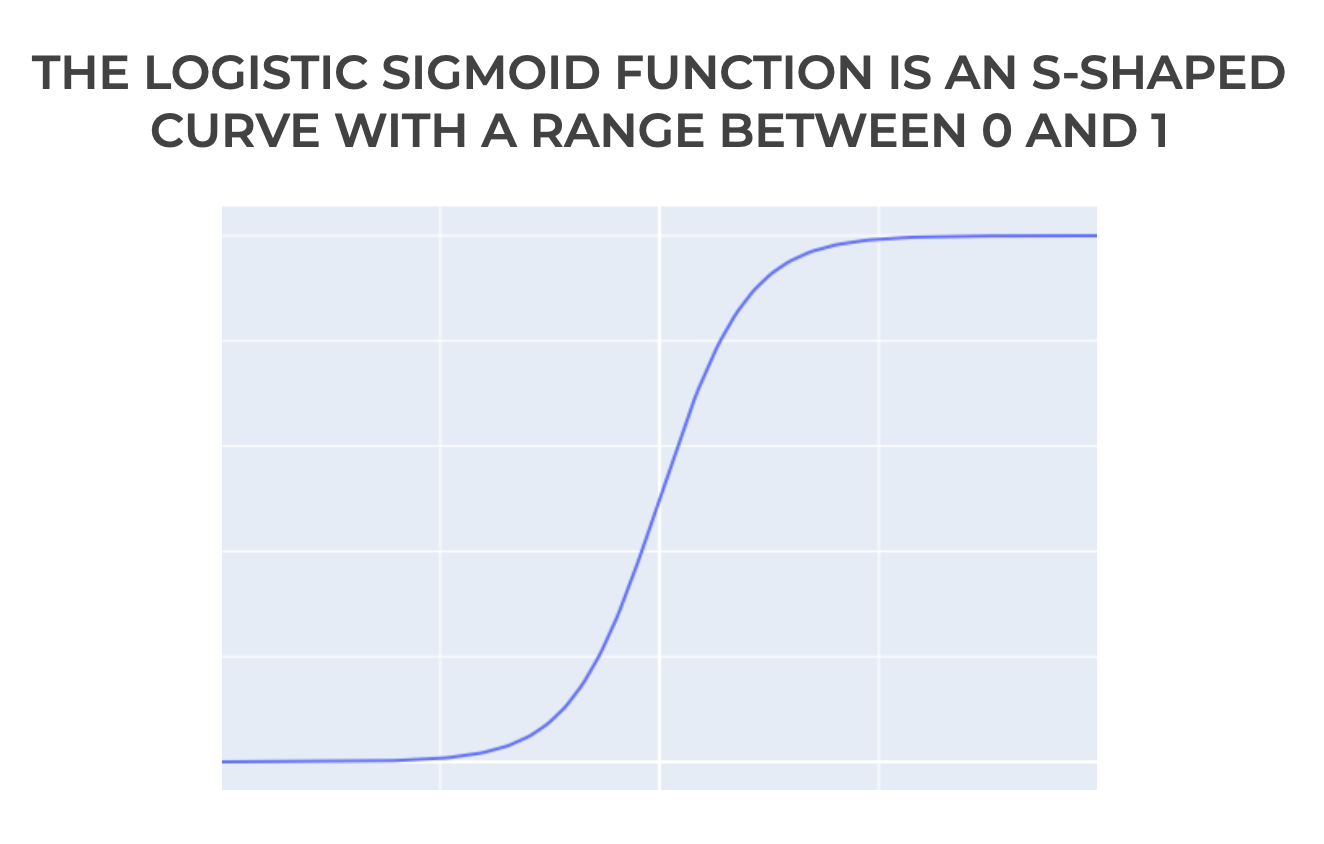
A simple visual example of a logistic sigmoid function.

这个sigmoid函数经常被用于机器学习中。特别是，它经常被用作深度学习和人工神经网络的激活函数。

既然它经常被用于机器学习和深度学习，那么知道如何在常见的机器学习编程语言中实现它就有潜在的意义。

既然如此，让我们看看如何在Python中实现这个函数，这是机器学习中最流行的编程语言之一。

Python Logistic sigmoid函数的语法

我们可以在Python中定义logistic sigmoid函数，如下所示。

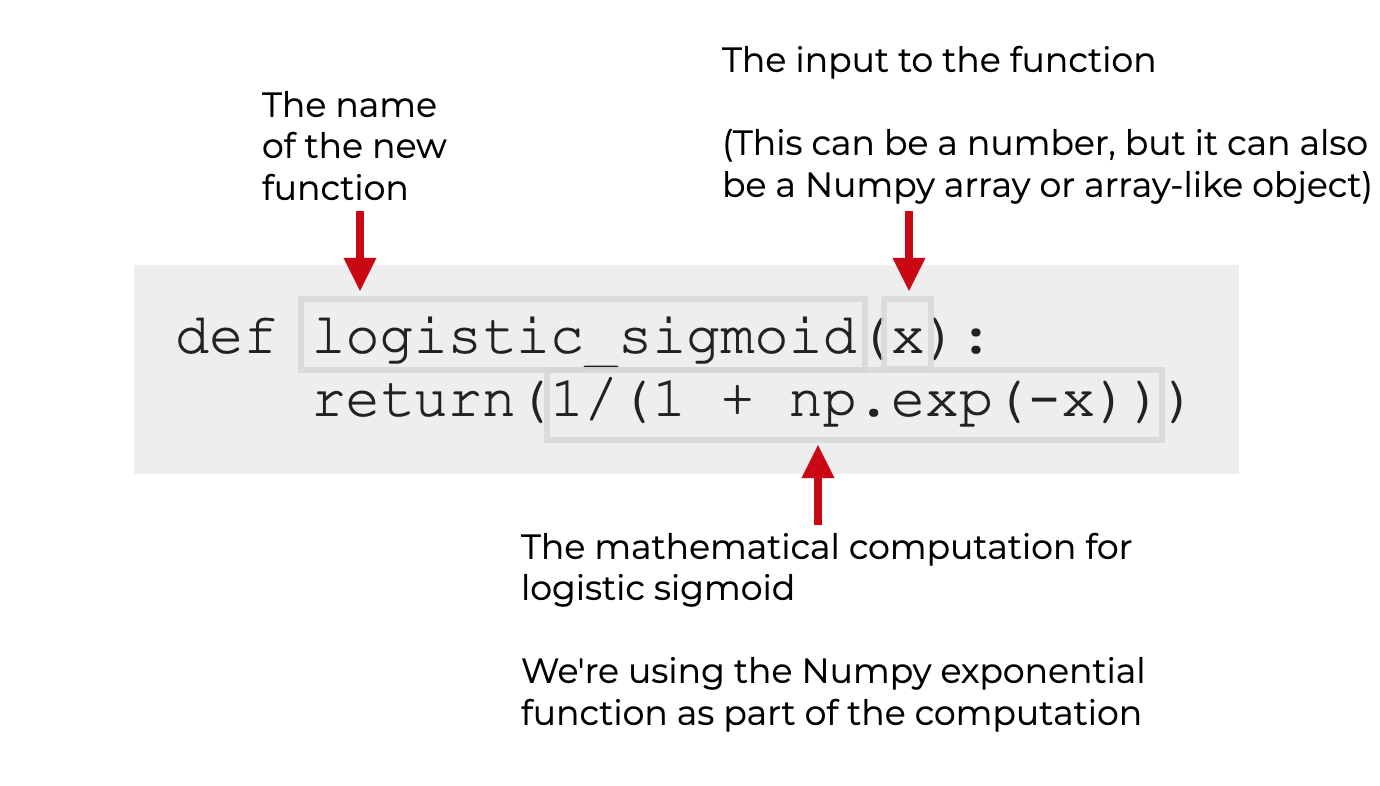
An image that shows a definition of the logistic sigmoid function in Python, with annotations and explanations.

(你也可以在例子1中找到Python代码)。

这里，def 关键字表示我们正在定义一个新的 Python 函数。

我们将这个函数命名为 "logistic_sigmoid" (尽管我们可以用别的名字来命名)。

输入值被称为 x

在函数的主体中，我们看到一个返回语句和其中的一个计算。这个计算正在计算值。

(2 ) 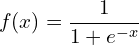$\begin{equation*} f(x) = \frac{1}{1 + e^{-x}} \end{equation*}$

...其中x是函数的输入值。

注意，为了执行这个计算，我们正在调用Numpy的指数函数。

输入值的格式

让我们来谈谈函数的可能输入值。

这个函数将对以下内容进行操作：

单一数字
Numpy数组
类似数组的对象 (如Python列表)

该函数的输出

输出将略有不同，取决于输入的类型。

如果输入的是一个数字，那么输出的将是一个数字。

如果输入是一个数组或类似数组的对象，那么该函数将输出一个Numpy数组。重要的是，输出数组将具有与输入相同的大小和形状。输出数组的值将是输入值的逐元计算结果。

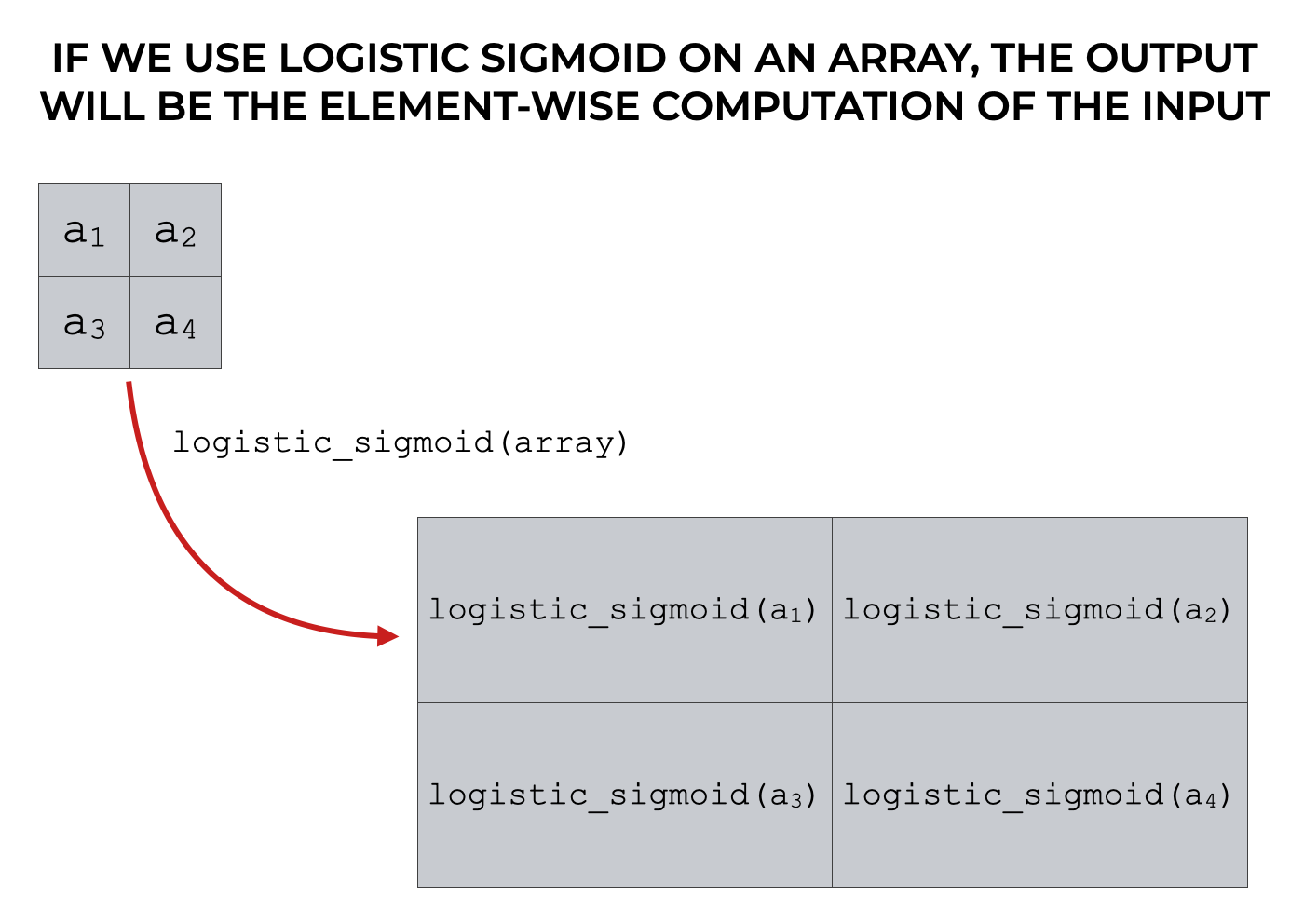
A visual example showing the logistic_sigmoid function operating on a Numpy array, where the output is the element-wise logistic sigmoid computation of the values of the input array.

例子：如何在Python中实现和使用Logistic sigmoid函数

现在我们已经看了如何实现logistic sigmoid函数的语法，让我们实际执行函数代码并在一些例子中使用它。

例子

定义Numpy logistic sigmoid函数
计算0的logistic sigmoid值
计算5的logistic sigmoid值
计算-5的logistic sigmoid值
在一个数组上使用logistic sigmoid
绘制logistic sigmoid函数图

初步代码，导入Numpy并设置Plotly

在你运行这些例子之前，你需要运行一些设置代码。

具体来说，你需要导入一些包，并设置Plotly来渲染图像。

导入软件包

首先，我们需要导入Numpy和Plotly express。

import numpy as np
import plotly.express as px

我们将在我们的函数实现中使用一个Numpy函数--np.exp。

而我们将在例子6中使用Plotly Express来绘制这个函数。

设置图像渲染

接下来，你可能需要配置Plotly来渲染你系统上的图像。

说白了：只有在你使用IDE的时候才需要这样做。

默认情况下，Plotly被设置为在浏览器窗口中渲染图像（即输出可视化）。如果你在笔记本上工作，这很好。但如果你在像PyCharm或Spyder这样的IDE中工作，它就会导致错误。

所以，你需要告诉Plotly在IDE中直接将其输出渲染成svg。

(注意：如果你使用的是Jupyter，你可以跳过这段代码！)

import plotly.io as pio
pio.renderers.default = 'svg'

运行完设置代码后，你应该准备好运行这些例子了。

例子1:用Python定义Logistic Sigmoid函数

首先，我们将在Python中定义logistic sigmoid函数。

def logistic_sigmoid(x):
    return(1/(1 + np.exp(-x)))

解释

这里，我们使用 Python 的def 关键字来定义一个新的函数。我们将这个新函数命名为 "logistic_sigmoid"。

这个函数有一个输入：x 。

该函数将返回以下结果。

(3 ) 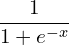$\begin{equation*} \frac{1}{1 + e^{-x}} \end{equation*}$

注意，我们是通过使用Numpy指数函数来计算这个输出的一部分。

实例2：计算0的对数西格玛值

现在我们已经定义了我们的函数，让我们来计算0的sigmoid值

logistic_sigmoid(0)

输出

0.5

例3：计算5的对数西格玛值

接下来，让我们计算5的二叉戟。

logistic_sigmoid(5)

输出

0.9933071490757153

解释

在这里，我们已经计算了5的logistic sigmoid。

请注意，该值非常接近于1。

这是预期的。当x上升到无穷大时，logistic sigmoid函数将收敛到1。

实例4:计算-5的logistic sigmoid值

现在，让我们来计算-5的sigmoid。

logistic_sigmoid(-5)

输出

0.0066928509242848554

解释

在这里，我们已经计算出了-5的sigmoid。

请注意，这个值非常接近于0。

这正如我们所期望的那样。当x上升到负无穷大时，函数将收敛于0。

例子 5:在一个数组上使用Logistic sigmoid函数

现在，我们将在一个数组上使用我们的sigmoid函数。

创建Numpy数组

首先，我们将创建一个Numpy数组。

特别是，我们要创建一个均匀间隔的数值数组。

为了做到这一点，我们将使用Numpy linespace函数，创建一个从-10到10的均匀间隔的数值阵列。

x_values = np.linspace(start = -10, stop = 10, num = 201)

让我们把它打印出来看一看。

print(x_values)

输出

[-10.   -9.9  -9.8  -9.7  -9.6  -9.5  -9.4  -9.3  -9.2  -9.1  -9.   -8.9  -8.8  -8.7  -8.6  -8.5  -8.4  -8.3  -8.2  -8.1  -8.   -7.9  -7.8  -7.7  -7.6  -7.5  -7.4  -7.3  -7.2  -7.1  -7.   -6.9  -6.8  -6.7  -6.6  -6.5  -6.4  -6.3  -6.2  -6.1  -6.   -5.9  -5.8  -5.7  -5.6  -5.5  -5.4  -5.3....   5.6   5.7   5.8   5.9   6.    6.1   6.2   6.3   6.4   6.5   6.6   6.7   6.8   6.9   7.    7.1   7.2   7.3   7.4   7.5   7.6   7.7   7.8   7.9   8.    8.1   8.2   8.3   8.4   8.5   8.6   8.7   8.8   8.9   9.    9.1   9.2   9.3   9.4   9.5   9.6   9.7   9.8   9.9  10. ]

为了节省空间，我对输出结果进行了一定程度的缩减。

但是如果你仔细观察，你可以看到，x_values ，包含了从-10到10的数值，增量为0.1。

计算Logistic Sigmoid值

现在，我们要在x_values ，使用我们的sigmoid函数。

logistic_sigmoid_values = logistic_sigmoid(x_values)

并让我们打印结果。

print(logistic_sigmoid_values)

输出

[4.53978687e-05 5.01721647e-05 5.54485247e-05 6.12797396e-05
 6.77241496e-05 7.48462275e-05 8.27172229e-05 9.14158739e-05
 1.01029194e-04 1.11653341e-04 1.23394576e-04 1.36370327e-04
 1.50710358e-04 1.66558065e-04 1.84071905e-04 2.03426978e-04
....
 9.99849290e-01 9.99863630e-01 9.99876605e-01 9.99888347e-01
 9.99898971e-01 9.99908584e-01 9.99917283e-01 9.99925154e-01
 9.99932276e-01 9.99938720e-01 9.99944551e-01 9.99949828e-01
 9.99954602e-01]

解释

我对结果进行了缩写，但在这里，我们可以大致看到结果中的内容。

如果你仔细观察，你可以看到一些非常接近0的值，也有一些非常接近1的值。

(我们一会儿在绘制数据时就会看到这一切）。

例子6:绘制Logistic Sigmoid函数图

最后，让我们绘制Logistic sigmoid函数。

具体来说，我们将绘制我们在例5中计算的输出值。

要做到这一点，我们将使用Plotly的直线函数px.line。

px.line(x = x_values, y = logistic_sigmoid_values)

输出

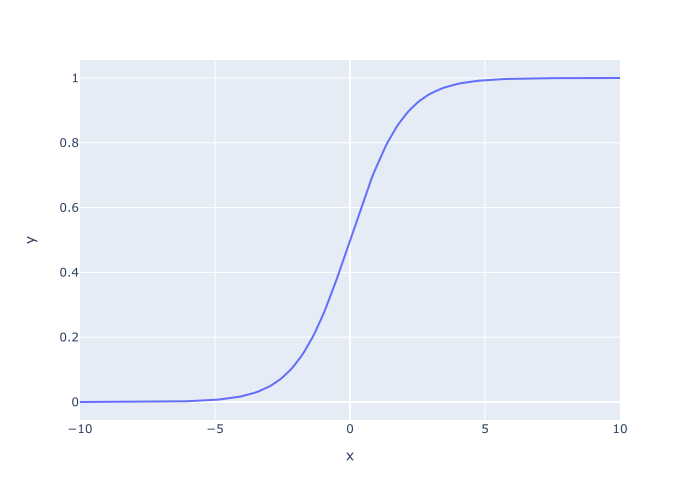
A simple image of the logistic sigmoid function, Plotted with px.line.

解释

在这里，我们用Plotly直线函数绘制了我们在例5中计算的logistic sigmoid值。

在x轴上，我们把包含在x_values 中的值绘制出来。

在Y轴上，我们映射了Numpy数组中的数值， logistic_sigmoid_values 。

最后的输出结果是我们的s型sigmoid函数的图。

在本教程中，我解释了如何在Python中使用Numpy来实现和使用logistic sigmoid。

Numpy Mastery将教会你关于Numpy的所有知识，包括：

如何创建Numpy数组
如何重塑、分割和组合你的Numpy数组
Numpy随机种子 "函数的作用是什么？
如何使用Numpy的随机函数
如何对Numpy数组进行数学运算
以及更多...