合并排序的最坏情况以及其时间复杂性分析

吴欣
942 阅读5分钟

在这篇文章中，我们介绍了合并排序表现最差的情况，如何识别这种最差情况的输入以及合并排序最差情况的时间复杂性分析。

内容：

  • 概述
  • 它是如何工作的
  • 最坏情况何时发生
  • 合并排序的最坏情况下的时间复杂性分析
  • 合并排序的实现
  • 总结

简而言之，合并排序的最坏情况是左右数组中的元素交替出现。这将导致最大数量的比较，时间复杂度保持在O(N logN)。

概述

合并排序是最有效的排序算法之一，它是基于分而治之的方法。基本上，在合并排序中，我们将输入数组分为两部分，然后通过递归调用自身对两部分进行排序，最后合并这两部分的排序。在合并排序中，通过递归对两部分进行排序后，我们调用合并函数，将两个排序后的子数组合并为一个。

它是如何工作的

让我们按以下步骤讨论合并排序的工作：
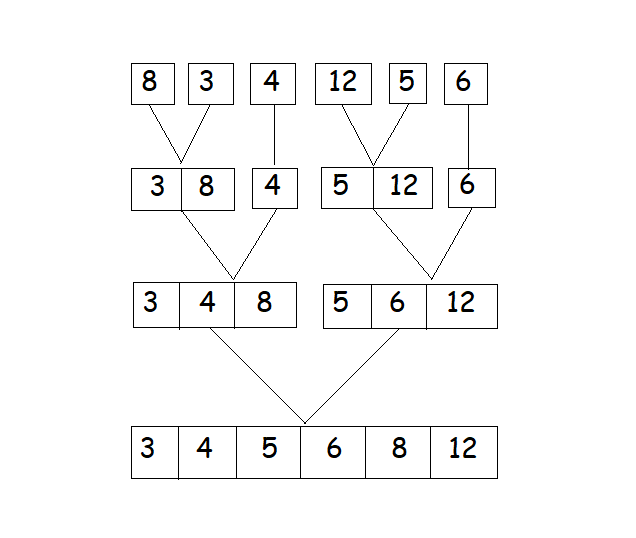
考虑一个数组={8,3,4,12,5,6}

  1. 首先，我们将通过确定中间索引将数组分成两半。
    midIndex = (startIndex + endIndex)/2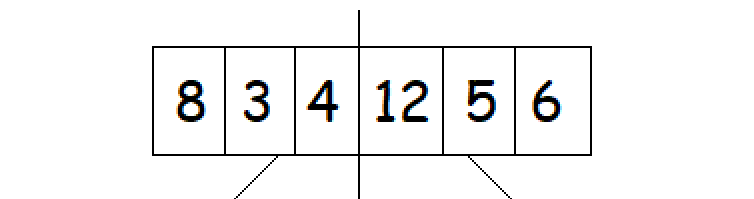

    Screenshot--1060-

  2. 我们将再次找到每个部分的中间索引，然后将每个部分分成后续的子数组。
    M2

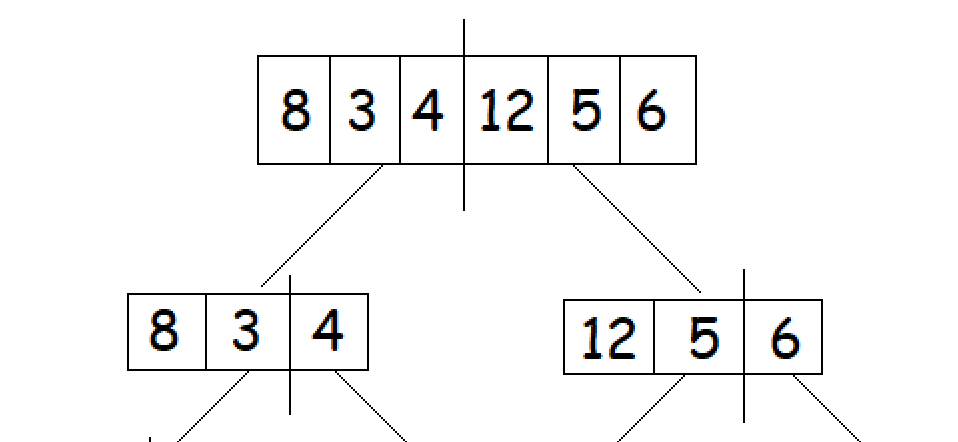
  3. 我们将继续通过寻找每个子数组的中间索引将数组分成两半，除非我们达到原子值，即该特定子数组中只剩下单个元素。
    m3

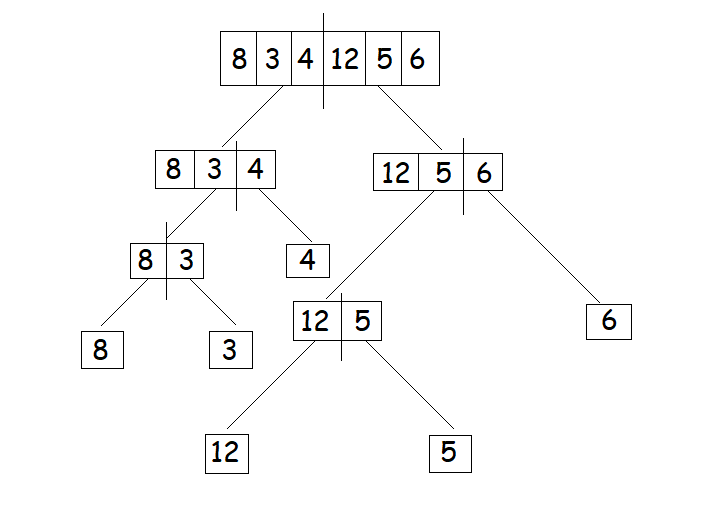
  4. 之后，我们将开始以排序的方式或根据元素大小的比较来合并最小的子数组。
    m4

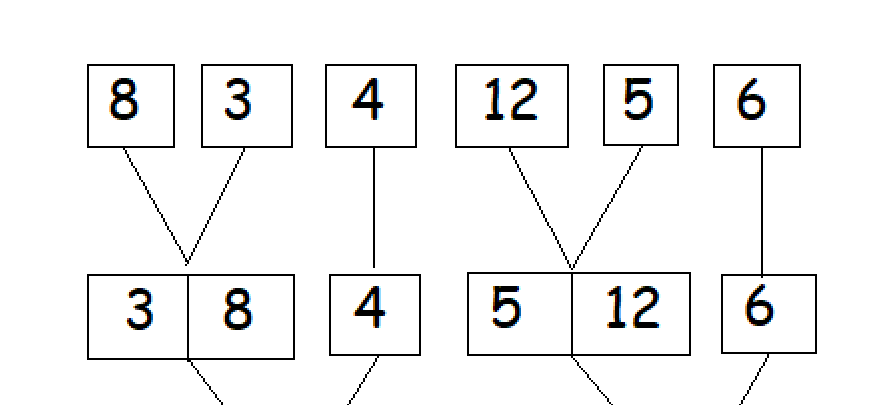
  5. 最后，在合并每个子数组后，最终结果将是这样的。
    m5

合并排序的算法。
mergeSort(arr, start, end)

如果大小>1

  • 找到输入数组的中间索引，这样我们就可以把数组分成两部分了
    • mid = arr.length / 2;
  • 对leftSubArray调用mergesort。
    • mergeSort(left, 0, mid)。
  • 调用右侧子数组的Mergesort函数
    • mergeSort(right, mid, arr.length);
  • 调用merge函数来合并这两半的数据
    • mergeTwoSortedArray(left, right)

最坏的情况何时发生？

合并排序的时间复杂度将取决于以排序方式合并子数组时进行的比较次数。因此，我们只有在减少比较次数的情况下才能提高时间复杂度。然而，有一种情况下，我们无法优化时间复杂度，当左右子数组都包含备用数字时，这种情况就会出现。

让我们举个例子来说明一下。

考虑，左边的子数组为{1,3,5,7}，右边的子数组为{2,4,6,8}。

在这个特殊的例子中，两个数组的每一个元素都需要至少比较一次，才能以排序的方式合并。因此，在合并子数组的过程中会有n次（输入数组的元素总数）比较。这将是最坏的情况，并将产生最坏的合并排序的时间复杂度。

现在，考虑一个排序的数字集[0, 1, 2, 3, 4, 5, 6, 7]。

         [4, 0, 6, 2, 5, 1, 7, 3]
               /  \
              /    \
    [4, 0, 6, 2]    [5, 1, 7, 3]
         / \           / \
        /   \         /   \
    [4, 0] [6, 2]   [5, 1] [7, 3]
       |     |        |     |
       |     |        |     |
    [0, 4] [2, 6]  [1, 5] [3, 7]
       \     /        \     /
        \   /          \   /
    [0, 2, 4, 6]    [1, 3, 5, 7]
          \             /
           \           / 
      [0, 1, 2, 3, 4, 5, 6, 7]

注意：在每一步中，左和右的子arrays都包含交替的数字。

所以，如果排序后的列表是[0, 1, 2, 3, 4, 5, 6, 7]，那么合并排序的最坏情况输入是[4, 0, 6, 2, 5, 1, 7, 3]。

 [0, 2, 1, 3]
   /     \
  /       \
[0, 2]  [1, 3]
  \       /
   \     /
 [0, 1, 2, 3]

因此，对于一个[0, 1, 2, 3]的排序列表，合并排序的最坏情况输入将是[0, 2, 1, 3]。

合并排序的最坏情况下的时间复杂性分析

我们可以将合并排序分为两个步骤。

  1. 使用递归将输入数组分成两半，这需要对数时间复杂度，即log(n)，其中n是输入数组中的元素数。
    让我们把T1(n)=划分数组的时间复杂度
    T1(n)=T1(n/2)+T1(n/2)
    T1(n)=2*T1(n/2)

  2. 通过比较子数组中的每个元素，将被分割的数组以排序的方式合并成一个数组。因此，在上面讨论的最坏情况下，在合并子数组时将进行n-1（输入数组中的元素数）的比较。

让我们把T2(n)=合并子数组的时间复杂度
T2(n)=n-1

因此，合并排序的总时间复杂度=T1(n) +T2(n)
让我们取T(n) = 合并排序的总时间复杂度
T(n) = 2*T(n/2) + n-1

使用Akra Bazzi公式来解决上述递归关系。

time
所以，对于给定的n大小的数组，合并排序的时间复杂度将是O(nlogn)。

合并排序的实现

我们已经知道，合并排序是基于分而治之的排序算法。
因此，下面给出的是合并排序在java编程语言中的实现。

合并排序的伪装代码

mergeSort(int[] arr)

     1. Find the middle point to divide the input into two halves:  
             middle = arr.length/2
     2. Call MergeSort for first half:   
             int[] left = mergeSort(Arrays.copyOfRange(arr, 0, mid));
     3. Call MergeSort for the other half:
             int[] rigth = mergeSort(Arrays.copyOfRange(arr, mid, arr.length));
     4. Merge the two halves sorted in step 2 and 3:
             Call Merge(left, right)

代码

import java.util.Arrays;

public class Merge_Sort {
    public static void main(String[] args) {
        int[] arr = {5, 4, 3, 2, 1};
        arr = mergeSort(arr);
        System.out.println(Arrays.toString(arr));
    }
    static int[] mergeSort(int[] arr) {
        if (arr.length == 1) {
            return arr;
        }

        int mid = arr.length / 2;

        int[] left = mergeSort(Arrays.copyOfRange(arr, 0, mid));
        int[] right = mergeSort(Arrays.copyOfRange(arr, mid, arr.length));

        return merge(left, right);
    }

    private static int[] merge(int[] first, int[] second) {
        int[] mix = new int[first.length + second.length];

        int i = 0;
        int j = 0;
        int k = 0;

        while (i < first.length && j < second.length) {
            if (first[i] < second[j]) {
                mix[k] = first[i];
                i++;
            } else {
                mix[k] = second[j];
                j++;
            }
            k++;
        }

        // it may be possible that one of the arrays is not complete
        // copy the remaining elements
        while (i < first.length) {
            mix[k] = first[i];
            i++;
            k++;
        }

        while (j < second.length)
        {
            mix[k] = second[j];
            j++;
            k++;
        }

        return mix;
    }

}

输出
output
在这里，我们可以看到在输出窗口中显示了一个排序的数组。

结语

在这篇文章中，我讨论了合并排序，其最坏情况下的时间复杂度是O(nlogn)，其中n是数组的输入大小。我还讨论了什么时候会出现最坏的情况，即：当左右两个子数组都包含备用数字时。

avatar
文章
阅读
粉丝