在本教程中,与Python中的数据分析有关,你将学习如何处理你的数据,当它不遵循正常分布时。处理非正态数据的一种方法是转换你的数据。在这篇文章中,你将学习如何在Python中进行Box-Cox、平方根和对数变换。
将右偏数据转换为正态分布
我们拥有的数据是正态形状的(也被称为遵循贝尔曲线),这对于我们可能想要进行的大多数参数测试来说是很重要的。这包括回归分析、双样本t检验,以及可以在Python中进行的方差分析,仅举几例。
概要
这篇文章将首先简要介绍一下你在学习本教程时需要做什么。在这之后,你将1)获得关于偏度和峰度的信息,2)简要介绍不同的转换方法。在转换方法之后的部分,你将学习如何使用Pandas read_csv导入数据。我们将通过创建直方图,得到偏度和峰度的度量,对示例数据集进行一番探索。最后,最后一节将涉及如何转换非正态数据。
前提条件
在本教程中,我们将使用Pandas、SciPy和NumPy。值得一提的是,在这里,你只需要安装Pandas,因为其他两个Python包是Pandas的依赖项。也就是说,如果你用pip安装Python包,它也会在你的电脑上安装SciPy和NumPy,无论你使用的是Ubuntu Linux还是Windows 10。注意,你可以使用pip来安装一个特定的版本,例如Pandas,如果你需要,你可以使用 conda或pip来升级pip 。
现在,如果你想安装单个软件包(比如你只想使用NumPy和SciPy),你可以运行以下代码。
pip install pandas
Code language: Bash (bash)
现在,如果你只想安装NumPy,在上面的代码中把 "pandas "改为 "numpy"。说到这里,让我们继续看关于偏度和峰度的部分。
倾斜度和峰度
简而言之,偏度是一种对称性的衡量标准。确切地说,它是对缺乏对称性的一种衡量。这意味着数字越大,你的数据就越缺乏对称性(不是正常的,也就是说)。另一方面,峰度是衡量你的数据相对于正态分布来说是重尾还是轻尾的一个指标。关于这两种测量方法的更多数学定义,请看这里。用直方图直观地检查数据的偏度或峰度的一个好方法是使用直方图。然而,请注意,当然也有不同的统计测试,可以用来测试你的数据是否是正态分布。
如何在Python中处理偏态数据?
处理右斜或左斜数据的一种方法是对我们的数据进行对数变换。例如,np.log(x) 将对Python中的变量x 进行对数转换。还有其他的选择,如Box-Cox和平方根变换。
如何转换左倾斜的数据?
处理左(负)倾斜数据的一种方法是反转变量的分布。在Python中,这可以用下面的代码来完成。
上述两个问题将在整个文章中得到更详细的回答(例如,你将学习如何在Python中进行对数转换)。在下一节中,你将了解三种常用的转换技术,你,以后也将学会应用这些技术。
变换方法
正如介绍中所指出的,我们将学习三种方法,我们可以用它们来转换偏离正态分布的数据。在本节中,你将对这三种变换技术以及何时使用它们进行简要介绍。
平方根法
平方根法通常用于你的数据是中等偏斜的情况下。现在使用平方根(例如,sqrt(x))是一种对分布形状有适度影响的变换。它一般用于减少右偏的数据。最后,平方根可以应用于零值,最常用于计数数据。
对数转换
对数是一种强烈的变换,对分布形状有重大影响。这种技术和平方根法一样,经常用于减少右偏度。然而,值得注意的是,它不能应用于零或负值。
盒式考克斯变换
正如你可能理解的那样,Box-Cox转换也是一种将非正态数据转换为正态的技术。 这是一个确定合适的指数(Lambda=l)的程序,用于转换偏斜数据。
其他替代方法
现在,上面提到的转换技术是最常用的。然而,还有很多其他的方法,也可以用来转换你的倾斜因变量。例如,如果你的数据是序数数据类型,你也可以使用正弦转换法。另一种你可以使用的方法叫做倒数法。这种方法,基本上是这样进行的。1/x,其中x是你的因变量。
在下一节中,我们将导入包含四个因变量的数据,这些因变量是正向和负向倾斜的。
数据实例
在本教程中,我们将对负倾斜(左)和正倾斜(右)的数据进行转换,我们将从CSV文件(Data_to_Transform.csv)中读取一个示例数据集。为了帮助我们,我们将使用Pandas来读取.csv文件。
import pandas as pd
import numpy as np
# Reading dataset with skewed distributions
df = pd.read_csv('./SimData/Data_to_Transform.csv')
Code language: Python (python)
这是一个有以下四个变量的例子数据集。
- 中度正偏斜(右偏斜)。
- 高度正偏斜"(右偏)。
- 中度负偏态(左偏态)。
- 高度负偏斜(左偏斜)。
我们可以通过使用info() 方法获得这些信息。这将给我们提供数据框架的结构。
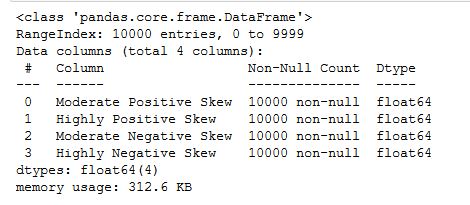
正如你所看到的,该数据框架有10000行和4列(如前所述)。此外,我们得到的信息是这4列都是浮动数据类型,而且数据集中没有缺失值。在下一节中,我们将快速查看我们的4个变量的分布。
在下一节中,我们将使用Pandas hist()函数对数据集中的变量做一个快速的视觉检查。
目视检查变量的分布
在这一节中,我们将直观地检查数据是否为正态分布。当然,有几种方法可以绘制数据的分布。然而,在这篇文章中,我们将只使用Pandas并创建直方图。下面是如何使用hist() 方法在潘达斯中创建直方图。
df.hist(grid=False,
figsize=(10, 6),
bins=30)
Code language: Python (python)
现在,hist() 方法将数据集中的所有数字变量(即,在我们的例子中是浮点数据类型),为每个变量创建一个直方图。为了快速解释上述代码块中使用的参数。首先,使用grid 参数并将其设置为False ,以从直方图中删除网格。其次,我们使用figsize 参数改变了图的大小。最后,我们还改变了bin的数量(默认是20),以获得更好的数据视图。下面是可视化的分布。
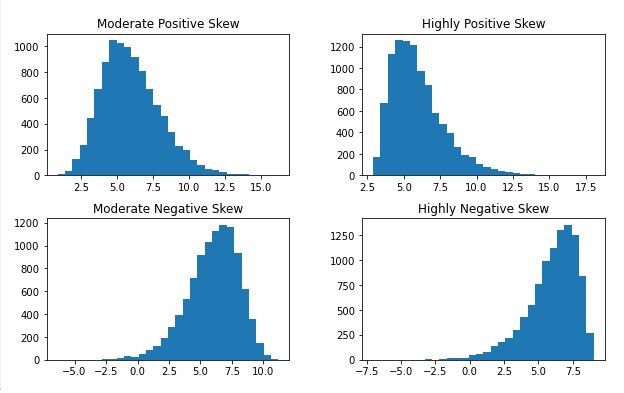
直方图显示右偏和左偏的变量。
很明显,所有的变量都是偏斜的,并不遵循正态分布(正如变量名称所暗示的)。注意,当然还有其他的可视化技术,你可以进行检查你的因变量的分布。例如,你可以使用boxplots、stripplots、swarmplots、kernel density estimation或者小提琴图。这些图给你提供了很多(更多)关于你的因变量的信息。在下一节中,我们还将看看如何获得偏度和峰度的测量。
Python中的偏度和峰度的测量方法
在这一节中,在我们开始学习如何在Python中转换倾斜数据之前,我们只需快速浏览一下如何在Python中获得偏度和峰度。
df.agg(['skew', 'kurtosis']).transpose()
Code language: Python (python)
在上面的代码块中,我们使用了agg() 方法,并使用一个列表作为唯一的参数。这个列表包含了我们想要使用的两种方法(即,我们想要计算偏度和峰度)。最后,我们使用transpose() 方法将行改为列(即转置Pandas数据框架),这样我们就得到了一个更容易检查的输出。下面是生成的表格。
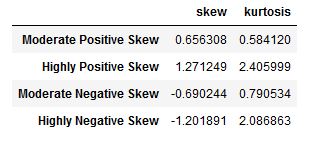
作为经验法则,偏度可以这样解释。
| 偏度 | |
| 相当对称 | -0.5到0.5 |
| 中度偏斜 | -0.5至-1.0和0.5至1.0 |
| 高度偏斜 | <-1.0和>1.0 |
当然,还有更多的事情可以做,以测试我们的数据是否是正态分布。例如,我们可以进行正态性的统计测试,如Shapiro-Wilks测试。然而,值得注意的是,大多数这些测试对于样本量来说是容易受到影响的。也就是说,使用例如夏皮罗-威尔克斯检验,即使是对正态性的微小偏离也会被发现。
在下一节,我们将开始转化非正态(偏斜)数据。首先,我们将转换中等偏斜分布,然后,我们将继续处理高度偏斜的数据。
Python中的平方根变换
下面是如何在Python中进行非正态数据的平方根变换。
# Python Square root transformation
df.insert(len(df.columns), 'A_Sqrt',
np.sqrt(df.iloc[:,0]))
Code language: Python (python)
在上面的代码块中,我们通过使用insert() 方法在Pandas数据框中创建了一个新的列/变量。此外,值得一提的是,我们使用iloc[]方法来选择我们想要的列。在下面的例子中,我们将继续使用这种方法来选择列。注意第一个参数(即":")是如何用来选择所有行的,第二个参数("0")是如何用来选择第一列的。另一方面,如果我们使用loc方法,我们可以通过列名来选择。下面是我们的新列/变量的直方图。
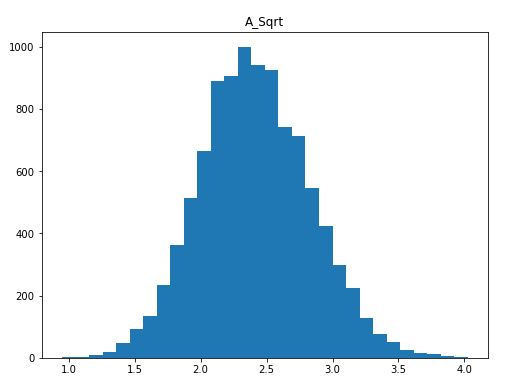
平方根转换后的分布
同样,我们可以看到,新的、经过Box-Cox变换的分布比以前的、右偏的分布更加对称。
在下一小节中,你将学习如何处理负(左)倾斜的数据。如果我们现在试图在这一列上应用sqrt(),我们会得到一个ValueError(见文章最后)。
用平方根方法转换负偏斜的数据
现在,如果我们想用平方根方法来转换负(左)倾斜的数据,我们可以这样做。
# Square root transormation on left skewed data in Python:
df.insert(len(df.columns), 'B_Sqrt',
np.sqrt(max(df.iloc[:, 2]+1) - df.iloc[:, 2]))
Code language: PHP (php)
我们在上面所做的,是将分布反转(即max(df.iloc[:, 2] + 1) - df.iloc[:, 2] ),然后应用平方根变换。你可以看到,在下面的图片中,当反转负偏斜分布时,偏度变成了正数。
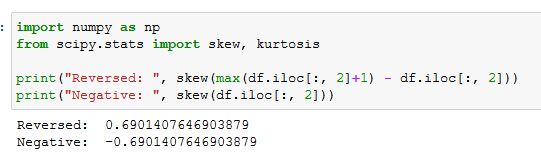
在下一节中,你将学习如何在Python中对高度偏斜的数据进行对数变换,包括向右和向左。
Python中的对数变换
下面是我们如何使用Python中的对数变换来使我们的偏斜数据更加对称。
# Python log transform
df.insert(len(df.columns), 'C_log',
np.log(df['Highly Positive Skew']))
Code language: PHP (php)
现在,我们的做法与使用Python进行平方根变换时基本相同。在这里,我们使用 insert() 方法创建了一个新的列。然而,这次我们使用了NumPy的log()方法,因为我们想做一个对数转换。下面是现在的分布情况。
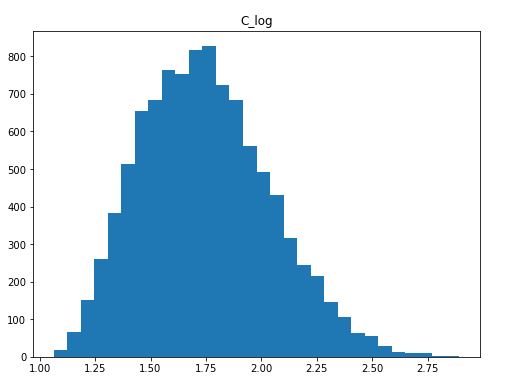
自变量在Python中进行对数转换
负偏态数据的对数转换
下面是如何在Python中对负偏斜数据进行对数变换的。
# Log transformation of negatively (left) skewed data in Python
df.insert(len(df.columns), 'D_log',
np.log(max(df.iloc[:, 2] + 1) - df.iloc[:, 2]))
Code language: PHP (php)
我们再次使用NumPy的log()方法进行了对数转换。此外,我们的做法与平方根的例子完全一样。也就是说,我们反转了分布,我们可以再次看到,所发生的一切是偏度从负数变成了正数。

在下一节,我们将看看如何使用SciPy对我们的数据进行Box Cox变换。
Python中的Box-Cox转换
下面是如何使用Python软件包SciPy来实现Box-Cox变换的。
from scipy.stats import boxcox
# Box-Cox Transformation in Python
df.insert(len(df.columns), 'A_Boxcox',
boxcox(df.iloc[:, 0])[0])
Code language: Python (python)
在上面的代码块中,基本上与前面的例子唯一不同的是,我们从scipy.stats ,导入了boxcox() 。此外,我们使用boxcox() 方法来应用Box-Cox变换。请注意我们是如何使用括号选择第一个元素的(即[0] )。这是因为这个方法(即boxcox() )会给我们一个元组。下面是对所产生的分布的可视化描述。
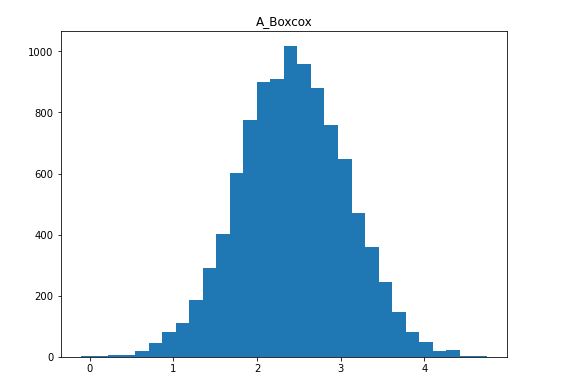
经箱形图转换的因变量的直方图
再一次,我们成功地将我们的正偏态数据转化为相对对称的分布。现在,Box-Cox变换也要求我们的数据只包含正数,所以如果我们想把它应用在负偏斜的数据上,我们需要把它反过来(见前面的例子,如何反转你的分布)。例如,如果我们试图在 "中度负偏态 "列上使用boxcox() ,我们会得到一个ValueError。
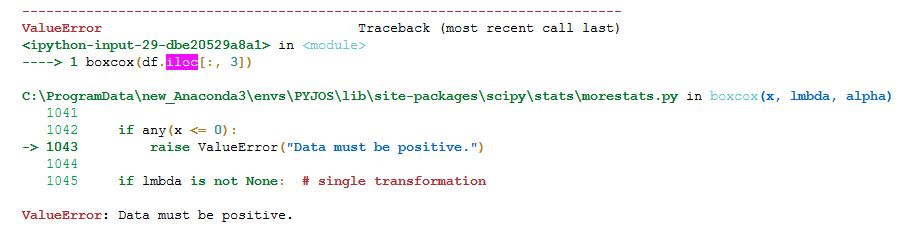
更确切地说,如果你得到 "ValueError:数据必须是正数",同时使用np.sqrt(),np.log() 或SciPy的boxcox() ,这是因为你的因变量包含负数。为了解决这个问题,你可以把分布反过来。
值得注意的是,在这里,我们现在可以使用skew() 方法检查偏度。
df.agg(['skew']).transpose()
Code language: Python (python)
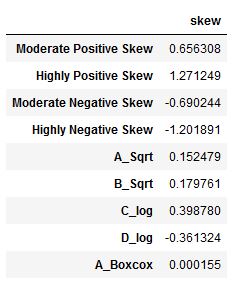
我们可以在输出中看到,转换后的数值的偏度值现在是可以接受的(它们都低于0.5)。当然,我们也可以运行前面提到的正态性测试(例如,Shapiro-Wilks测试)。注意,如果你的数据仍然不是正态分布,你也可以在Python中进行Mann-Whitney U检验。
总结
在这篇文章中,你已经学会了如何使用Pandas、SciPy和NumPy在Python中应用平方根、对数和Box-Cox转换。具体来说,你已经学会了如何转换正(左)和负(右)倾斜的数据,使其符合正态假设的条件。首先,你在上面简单地学习了将非正态和偏态数据转化为正态分布数据所需的Python软件包。其次,你了解了三种方法,后来你也学会了如何在Python中进行。