本文已参与「新人创作礼」活动,一起开启掘金创作之路。
线性回归函数
hθ(x(i))=θ1x(i)+θ0
其中i =1,2,……,m表示样本
损失函数
J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
21 在这里是为了之后求导运算,将系数归1
函数图形如图
1. 对损失函数求偏导
∂θj∂J(θ0,θ1)=m1i=0∑m(hθ(xi)−yi)∂θj∂(hθ(xi)−yi)=m1i=0∑m(hθ(xi)−yi)∂θj∂(yi−j=0∑nθjxji)=m1i=0∑m(hθ(xi)−yi)xji
其中j=0,1表示特征数,i表示样本数,x0i=1 (用F代替偏导数)
2. 每次迭代同步更新θ1θ2
θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
temp1 = θ1-αF
temp2 = θ2-αF
θ1 = temp1
θ2 = temp2
每次更新θ值,图像上的点会向梯度反方向移动,同时意味着θ值也不断接近最小值靠近。当θ值不变时,也就意味着此时导数为0,到达最小值
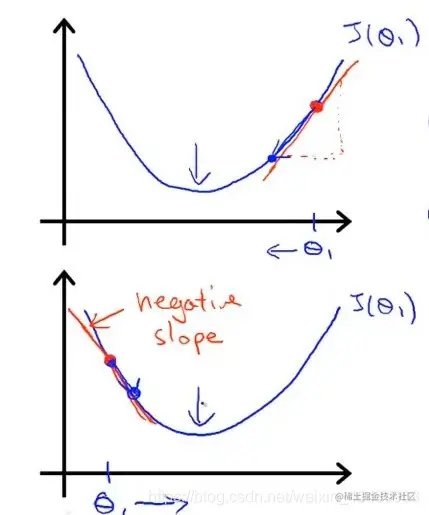
3. 不同学习率α值对于整个梯度下降过程的影响
当α值过小时,每次下降的程度非常小,导致接近最小值的过程较长
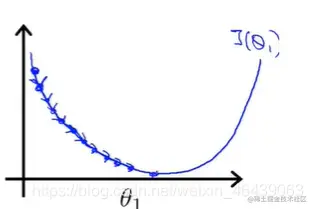
当α值过大时,每次步幅下降程度较大,会导致容易错过,最优解,最终反而导致无法 收敛甚至发散
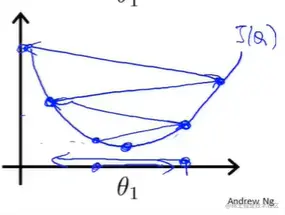
对于α值的选择可以通过损失函数的最小值变化与迭代次数的走势来观察,正常情况会一直下降不断趋于平缓,若反而上升或者来回波动,则说明α值可能取值较大,试着换更小值
注意
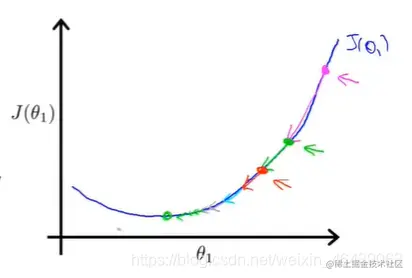
即使α值不变时,也可以通过梯度下降不断迭代到最小值。当θ值较大时,所计算的到的梯度值也较大,此时如粉色,下降较大的一步,而此后,新的θ值所计算得到的偏导值会不断减小,也就是说函数图像下降的比较缓慢,此时下降的步幅也就较小。
所以并不一定需要在迭代的过程中修改α值
此方法属于贪心算法的一种,所以容易陷入局部最优解,而无法取得全局最优。最终结果取值与初始值的选取关系很大。
当然,若是凸函数只有一个最优解,则局部最优解也是全局最优解
另外Batch意味着每次迭代更新参数时,都需要计算所有数据,所以才被称作批处理,数据量大时,计算时间会较长
附矩阵方程直接求解
ΘΘ=(XTXXTX)−1XTYXTY