• 原文地址：Solving Word Hunt in Python: The Trie
• 原文作者：Citizen Upgrade
• 译文出自：掘金翻译计划
• 本文永久链接：github.com/xitu/gold-m…
• 译者：TrWestdoor
• 校对者：zenblo, jackvin

用 Python 完成猎词游戏：字典树

猎词（word hunt）是一类很常见的游戏，给你一张字母组成的表，然后让你在这些字母中尽可能多的去寻找单词。关于这个游戏有不同的类别，一类是你可以多次重复使用这些字母（这类游戏叫做猎词），或者你只能使用一次每个字母（这类游戏叫做字母重组）。你组出来的单词越长就得分越高，使用了所有字母就可以获得最高分。

这类游戏对计算机而言是很容易去完成的，而且要强调一个相当有用的数据结构叫做“Trie”。

解决策略

让我们先拿出一个单词 MAINE。

首先要做的事就是分析这个问题的解决办法。如果问题是字母重组，那么我们可以尝试所有可能的字母组合，然后看看它们是否是单词。这对字母重组是一个还不错的解决方案，但是对猎词而言就不能给我们多少帮助了，因为字母可以被重用。所以当你可能发现了单词“name”时，你将再不会发现单词“nine”。显然我们不能尝试穷尽这些字母所有可能的组合，因为我们不知道一个单词可能被重复多少次。因为这个原因，我们退步为搜索一个词典，去看这个词是否可以只由我们拥有的字母组成。当有一个很大的词典时，这可能耗费大量的时间，并且你每次换了一个词时都必须重复这一步。

作为替代，我们需要一个搜索词典的方法，可以快速告诉我们某个单词是否在词典中。这就是预测性文本结构 Trie 字典树的用武之地。

什么是 Trie？

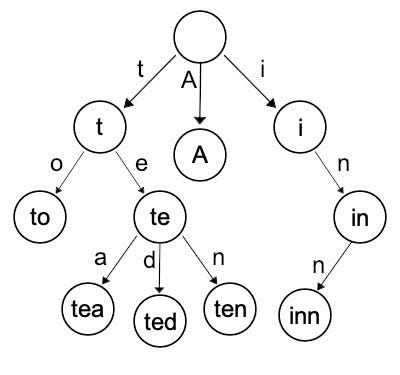
Trie 是一个树数据结构 — 其中的节点关联 key 本身，而不是关联与 key 关联的 value。节点中的值可用于根据遍历次数来为某些叶子节点或概率值分配顺序。

上面这个 Trie 的例子由“A”，“to”，“tea”，“ted”，“ten”，“i”，“in”和“inn” 生成。只要是生成一个像这样的 Trie 字典树结构，去判断任何一个单词是否在这个 Trie 字典树中就是 O(n) 复杂度的。如果我在搜索“ted”，我会消耗 O(1) 去寻找“t”，然后从 “t” 节点再消耗 O(1) 去寻找“e”，并且再从“te”节点消耗 O(1) 去到“d”。

应对“这些字母是否在词典中”的问题，就需要一个非常快速的解答方案。我们首先要做的就是构建词典。

在 Python 中，这个步骤很简单。每个节点的结构都应该是一个词典。所以我们需要从一个空词典开始，然后对词典中的每一个单词，逐字母的检查下一个字母是否在我们的 Trie 字典树结构中，如果不在就添进去。现在，这听起来相当耗费时间，在某些方面也的确如此，但是它只需要完成一次。当 Trie 被建好后，你可以直接使用它而无需任何其它开销。

创建 Trie 字典树

我们需要从一个装满所有可能单词的列表开始（网上有很多这类资源），然后我们的词典加载函数可能长下面这样：

def load():
    with open('words.txt') as wordFile:
        wordList = wordFile.read().split()
 
    trie = {}
    for word in wordList:
        addWordToTrie(trie, word)
   
    return trie

我们需要一个函数来给 Trie 中添加单词。我们通过快速浏览 Trie 来检查每一个字母，判断我们是否需要添加一个新的 key。因为我们通过 key 来检索 python 中的字典，所以无需在每个节点储存一个 value。 这是自带 key 值的新词典。

def addWordToTrie(trie, word, idx = 0):
    if idx >= len(word):
        return       
    if word[idx] not in d:
        d[word[idx]] = {}
    addWordToTrie(d[word[idx]], word, idx+1)

这里有一个简单的想法。我们接收的参数是当前所在位置的 Trie 字典树（注意在这个例子中，Trie 中的所有节点也是一个 Trie），这个单词，以及我们所查看的字母在单词中的索引。

如果索引超过了单词的长度，我们就停止！如果没有超过，我们需要检查是否这个字母已经在这个 Trie 中。如果这个字母不在这个 Trie 的下一层中，那么我们添加一个新的字典在这一层，当前这个字母就是字典的 key。然后，我们递归的调用这个函数，并且传入我们当前字母对应的词典（也就是 Trie），这个单词，以及下一个索引位置。

使用这两个函数，我们就构建了上面展示的 Trie 字典树。但是有一个问题摆在我们面前：如何判断我们找到的是一个单词，而不是一个真实单词的前一部分呢？例如，在上面这个 Trie 的例子中，我们希望“in”可以像“inn”一样返回是一个单词，但是并不希望将“te”作为一个词典中的单词来返回。

为了完成这一点，当我们完成一个单词时，必须在这个节点中储存一个值。来回头重新审视一下我们的 addWordToTrie 函数，如果这个节点表示一个完整的单词，就将“leaf”这个 key 设置为“True”。

def addWordToTrie(d, word, idx):
    if idx >= len(word):
        d['leaf']=True
        return
    if word[idx] not in d:
        d[word[idx]] = {'leaf':False}
    addWordToTrie(d[word[idx]], word, idx+1)

现在，无论何时我们完成一个单词，都要设置当前这个词典节点的“leaf”值为 True，或者我们添加一个新的节点，它的“leaf”值为“False”。

当我们加载这个函数初始化时，应该是同样的设置 {‘leaf’：False}， 因此我们以后不再将空字符串作为有效词返回。

就是这样！我们已经创建了我们的 Trie 结构，接下来是时候使用它了。

单词测试

找一个办法来进行尝试：从一个空的列表开始。对我们单词中的每个字母，检查我们的 Trie 字典树，看它是否在其中。如果在，就拿到这个词典子树再重新开始（这样我们可以检查重复的字母）。保持这样进行下去，直到我们找到一个 leaf 标志位为 true 的节点，或者我们在下一层的词典子树中找不到单词中的任何字母。如果我们发现了一个标记为 leaf 的节点，就把这个单词添到列表中。如果我们没有找到下一个词典子树，就返回并对下一个字母进行上述过程。

def findWords(trie, word, currentWord):
    myWords = [];
    for letter in word:
        if letter in trie:
            newWord = currentWord + letter
            if (trie[letter]['leaf']):
                myWords.append(newWord)
            myWords.extend(findWords(trie[letter], word, newWord))
    return myWords

这里注意一下，我们正在构建一个新单词传递到列表中，但是我们也会递归的去寻找新的单词，用来扩展我们的列表。

有的读者可能已经发现了接下来的问题。如果字母重复怎么办呢？例如我们的单词是“TEEN”，并且我们现在在“TE”节点上，我们已经在子树上检查了“t”，这很好，然后我们在子树上检查“e”并发现“tee”是一个单词。我们将“tee”添加到列表中。但是单词的下一个字母又是“e”，所以我们再次找到了“tee”。有一些方法去解决这个问题，但是最简单的方法之一就是用集合代替列表。

def findWords(trie, word, currentWord):
    myWords = set()      
    for letter in word:
        if letter in trie:
            newWord = currentWord + letter
            if trie[letter]['leaf']:
                myWords.add(newWord)
            myWords = myWords.union(findWords(trie[letter], word, newWord))
    return myWords

现在无论我们把同一个单词找到多少次，我们都可以保证列表中的唯一性。我们也可以将输入单词中的字母去重，进而节约处理时间。

就这样！利用这三个函数就可以通过我们输入的字母来找到所有可能在字典中的单词。来让我们把这些包到一个 main 函数里面，然后给一个输入，具体步骤我们已经完成了。

def main():
    print('Loading dictionary...')
    wordTrie = load()
    print('Done\n')
 
    word = raw_input("What letters should we use: ")
    minLength = int(raw_input("What is the minimum word length: "))
    print("")
 
    count = 0;
    for word in sorted(findWords(wordTrie, word, "")):
        if len(word) >= minLength:
            count = count+1
            print(word)
    print(str(count) + " words found.")

因为我们不是单词重组，所以我们找到了大量单词。使用上面提到的例子MAINE和一个我找到的词典 — 大约有 370000 个单词 — 这个程序发现了 208 个单词。这也是为什么我添加了一个最短单词长度的原因。限制单词长度至少为七，我们可以得到如下结果：

Loading dictionary…

Done

What letters should we use: maine

What is the minimum word length: 7

amninia

anaemia

anamnia

animine

emmenia

enamine

manienie

mannaia

meminna

miminae

minaean

11 words found.

加载词典消耗了大约半秒，后面的查找单词基本上感受不到明显的时间消耗。

为了一个单词去每次都重新建树是很低效的，所以最好可以重用它，要么是保存整个数据结构，要么尝试一次循环的查找多个单词。

总结

但愿这篇文章可以为你提供一个 Trie 的基本介绍，便于你去解决一些单词问题。当你想要一些自动补充完成的任务时，Trie 是一个很好用的数据结构。短信，搜索甚至是指引方向，都可以使用系统中的数据构建 Trie 来帮助预测用户下一步想要输入什么。正如我们所看到的，它也是在一个搜索大量的现有路径时很好的结构，在这个例子中，这个路径就是有效的单词。

如果发现译文存在错误或其他需要改进的地方，欢迎到 掘金翻译计划 对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

---

掘金翻译计划 是一个翻译优质互联网技术文章的社区，文章来源为 掘金 上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注 掘金翻译计划、官方微博、知乎专栏。