图解Multi-Head Attention | 多头注意力

Ann_
511 阅读2分钟

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第11天，点击查看活动详情

注意： 本篇文章需要结合Self-Attention | 自注意力 - 掘金 (juejin.cn)

在self-attention里我们提到，它的原理更类似于如何在序列模型中使用CNN的窗口，实现某个位置的注意力。我们说对于有多个意象的词，比如l’Afrique，我们要看看更关注哪一方面的含义。提取一方面的含义我们可以称之为一个头，如果要计算多方面的含义我们就可以称之为多头（multi-head）。

还是以这句话为例子： Jane visite l’Afrique en septembre.

先回顾一下self-attention中我们说，对于输入x，我们学习不同的参数将其转化为q,k,v。 例如l’Afrique:

q<3>=WQx<3>k<3>=WKx<3>v<3>=WVx<3>\begin{aligned} q^{<3>} &=W^{Q} x^{<3>} \\ k^{<3>} &=W^{K} x^{<3>} \\ v^{<3>} &=W^{V} x^{<3>} \end{aligned}

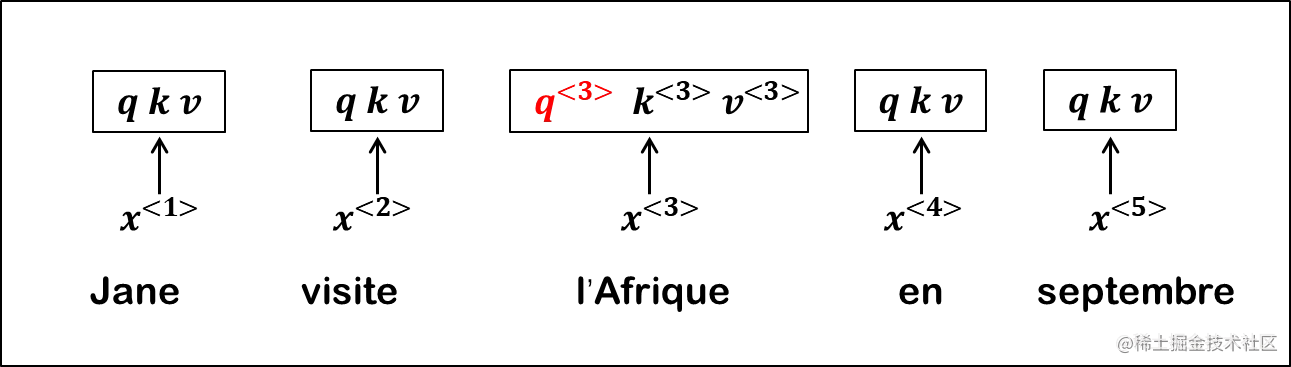
image.png

之后将当前位置的q和每一个k做运算。这一步可以根据q找到当前位置最相关的数据。

image.png

之后我们将所有的q和k的内积与v做计算并进行softmax。

l’Afrique为例，在这个句子里更关注其地理位置的属性，或者说旅游相关的方面，引发这个关注的词是visite。在这我们将最相关的标红。

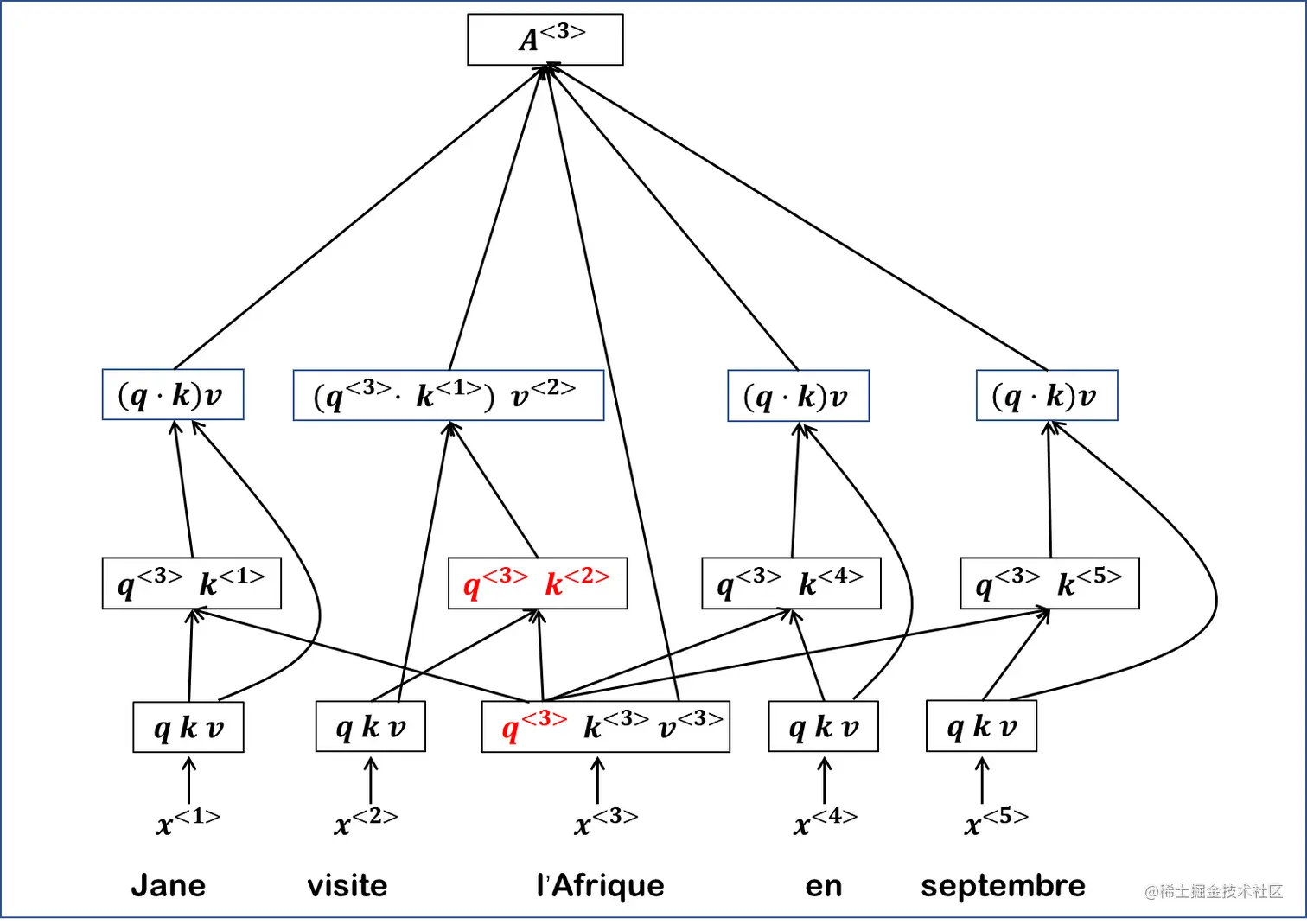
image.png

到这里我们就提取出了l’Afrique（非洲）的一个意象（一个head），如果我们要提取多面的意向就要计算多头注意力，这里稍微有一点区别：

首先我们依旧像之前一样获得query、key、value向量。

image.png

之后我们要计算出每个头自己的query、key、value向量。

还是以l’Afrique为例子，x<3>x^{<3>}的query、key、value向量要乘以第一个head对应的可学习参数，得到第一个head所需要的query、key、value向量。

q1<3>=W1Qq<3>k1<3>=W1Kk<3>v1<3>=W1Vv<3>\begin{aligned} q^{<3>}_{1} &=W^{Q}_{1} q^{<3>} \\ k^{<3>}_{1} &=W^{K}_{1} k^{<3>} \\ v^{<3>}_{1} &=W^{V}_{1} v^{<3>} \end{aligned}

image.png

head1计算出来之后其他的head计算方法一样。

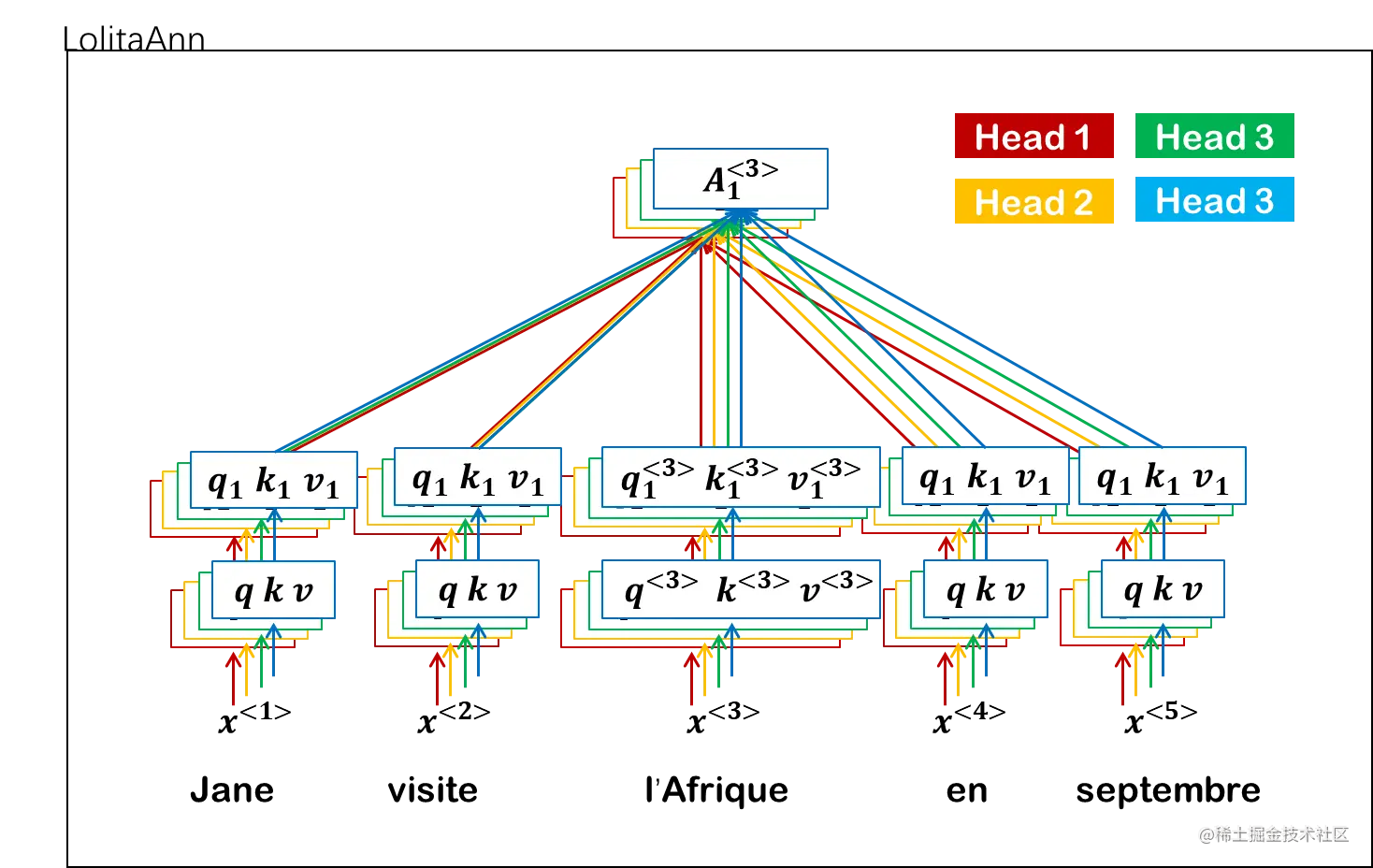
image.png

最后总结一下计算过程：

由输入获得query、key、value向量。

q<i>=WQx<i>k<i>=WKx<i>v<i>=WVx<i>\begin{aligned} q^{<i>} &=W^{Q} x^{<i>} \\ k^{<i>} &=W^{K} x^{<i>} \\ v^{<i>} &=W^{V} x^{<i>} \end{aligned}

获得每个head单独的query、key、value向量：

qj<i>=WjQq<i>kj<i>=WjKk<i>vj<i>=WjVv<i>\begin{aligned} q^{<i>}_{j} &=W^{Q}_{j} q^{<i>} \\ k^{<i>}_{j} &=W^{K}_{j} k^{<i>} \\ v^{<i>}_{j} &=W^{V}_{j} v^{<i>} \end{aligned}

query、key进行计算，获得距离：

qj<i>⋅kj<1>qj<i>⋅kj<2>...qj<i>⋅kj<i−1>qj<i>⋅kj<i+1>...qj<i>⋅kj<n>\begin{aligned} &q^{<i>}_{j} · k^{<1>}_{j} \\ &q^{<i>}_{j} · k^{<2>}_{j} \\ &...\\ &q^{<i>}_{j} · k^{<i-1>}_{j} \\ &q^{<i>}_{j} · k^{<i+1>}_{j} \\ &...\\ &q^{<i>}_{j} · k^{<n>}_{j} \\ \end{aligned}

上一步计算的值与对应的value做计算，之后将其相加获得注意力分数：

(qj<i>⋅kj<1>)vj<1>(qj<i>⋅kj<2>)vj<2>...(qj<i>⋅kj<i−1>)vj<i−1>(qj<i>⋅kj<i+1>)vj<i+1>...(qj<i>⋅kj<n>)vj<n>\begin{aligned} &(q^{<i>}_{j} · k^{<1>}_{j})v^{<1>}_{j} \\ &(q^{<i>}_{j} · k^{<2>}_{j})v^{<2>}_{j} \\ &...\\ &(q^{<i>}_{j} · k^{<i-1>}_{j})v^{<i-1>}_{j} \\ &(q^{<i>}_{j} · k^{<i+1>}_{j})v^{<i+1>}_{j} \\ &...\\ &(q^{<i>}_{j} · k^{<n>}_{j})v^{<n>}_{j} \\ \end{aligned}
attentionscorej<i>=(qj<i>⋅kj<1>)vj<1>+...+(qj<i>⋅kj<i−1>)vj<i−1>+vj<i>+(qj<i>⋅kj<i+1>)vj<i+1>+...+(qj<i>⋅kj<n>)vj<n>\begin{aligned} attention \quad score^{<i>}_{j} = &(q^{<i>}_{j} · k^{<1>}_{j})v^{<1>}_{j} + ... + (q^{<i>}_{j} · k^{<i-1>}_{j})v^{<i-1>}_{j} + \\ &v^{<i>}_{j}+(q^{<i>}_{j} · k^{<i+1>}_{j})v^{<i+1>}_{j} +... + (q^{<i>}_{j} · k^{<n>}_{j})v^{<n>}_{j} \end{aligned}

最后对其进行softmax计算：

Aj<i>=softmax(attentionscorej<i>).A^{<i>}_{j} = softmax(attention \quad score^{<i>}_{j}).
avatar
文章
阅读
粉丝