机器学习—隐马尔科夫模型(2)

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第2天，点击查看活动详情

评估问题

平时总是跟着学习，很少问为什么和进一步展开。今天我就想一想，解评估这样问题可以应用到哪些场景。其实我们根据过去观测序列加上可能预测的值作为一个观测序列，通过遍历所有下一个估计值可能来遍历概率，从中选择概率大多对应的值来作为对下一个时刻估计值。

先从相对比较简单问题开始，也就是评估问题，当拿到一个序列 $O=\{o_1,o_2,\cdots,o_T\}$ 这是观测到的数据，然后需要计算这个序列出现概率是多大，那么

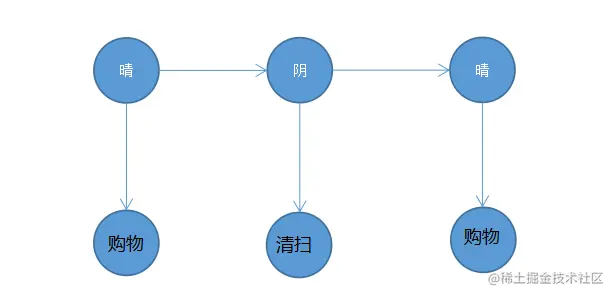
现在来看我们观测到序列为 $购物 \rightarrow 清扫 \rightarrow 购物$ 然后计算这个序列概率。对于这个问题，观测变量背后的隐含变量我们是看不到的，而且这个也不需要知道正确答案，例如，观测到一个观测值为购物，那么购物可能是从晴天或者阴天，首先计算某一个时刻是晴天和阴天的概率，这个是由上一状态到当前状态的状态转移概率所，然后在计算每一个状态生成对应观测值。

我们先用数学语言来描述一下，参数 $\lambda=[\pi, A, B]$ 和观测序列 $O = (o_1,o_2,\cdots, o_T)$ 求解观测序列出现的的概率 $P(O|I,\lambda)$，基本方法就是列举出所有可能的状态 $I = (i_1,i_2,\cdots,i_T)$ 接下来要求解的就是 $P(O,I|\lambda)$

$P(O,I|\lambda)$ 表示观测序列的出现概率，其实这个问题解起来并不难，

我们首先需要将所有可能隐含状态序列遍历出来，然后根据状态转移矩阵来计算出每条的概率，也就是 $P(I|\lambda)$

对于一个隐含状态序列 $I=(i_1,i_2,\dots,i_T)$ 出现的概率是，也就是出现某一条隐含状态序列的概率，这里 $i_1$ 表示某一个状态的随机变量。$i_1$ 取值是 Q 的某一个状态值，

通过贝叶斯或者联合概率可以得到 $P(O,I|\lambda) = P(O|I,\lambda)P(I|\lambda)$，

不过这样计算过程存在许多冗余计算，可以采用递归方式来避免重复计算，接下来

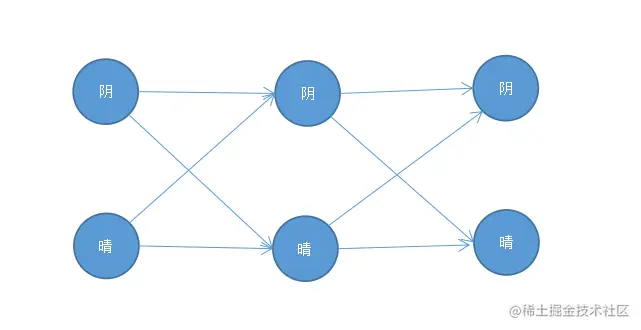
这里仅有 2 种隐状态，3 个时刻组成序列，那么排列组合有

会有 $2^3 = 8$ 排列组合，实际问题

前向算法

，也就是隐含变量，分别求解各个状态序列和观测序列的联合概率 $P(O,I|\lambda)$

也就是从初始状态 $\pi_{i1}$ 这里 $i$ 表示从 $i_1$ 表示在 1 时刻的状态概率，$a_{a_1,i_2}$ 表示从 $i_1$ 状态转移到 $i_2$ 状态概率，所以 $P(I|\lambda)$ 是序列 $I$

对于其中一种状态序列，观测序列的概率是，就是根据 $i_1$ 表示某一个状态，$b_{i1}(o_1)$ 表示观测。

总结上面公式，$P(I|\lambda)$ 来计算序列状态之间的转移概率联乘，$P(O|I,\lambda)$ 表示在某一个状态下乘以生成概率。

也就是遍历所有可能的隐含序列 $$

所谓前向计算也就是一层一层地计算，从而避免重复计算

前向概率，给定隐马尔可夫模型 $\lambda$ 参数前提，定义到时刻 $t$ 时刻部分观测序列为 $o_1,o_2,\dots,o_t$ 状态 $q_t$ 的概率为前向概率。前向概率对应某 $t$ 时刻 $j$ 状态，例如 $a_{t+1}(i)$ 表示在 $t+1$ 时刻，$i$ 状态概率，在 $t$ 时刻

计算初值

也就是计算第一时间处于各个隐状态的概率分布，

等式右边表示最初第 $i$ 个状态出现的概率，$\pi_i$ 表示 $i$ 状态其实概率，然后乘以从 $i$ 状态发射概率 $b_i(o_1)$。

迭代步骤

引入动态规划的思想，也就是问题分解一些小的问题，这些小的问题。中间步骤，在 $t+1$ 时刻 $i$ 状态的前向概率，是首先将 $t$ 时刻 $j$ 状态都乘以 $a_{ij}$

最后步骤

最后步骤就是将每一个节点的前向概率进行汇总求和，作为观测序列的评估概率。