CHUD算法

Suarne
1,290 阅读7分钟

写在前面：传统的高效用项集挖掘算法从数据集中挖掘海量的高效用项集，但这在一定程度上会给使用者造成一定的信息干扰，无法快速找出最重要的关键信息。为了解决这个问题，需要一种算法能够提供更简洁且有效的挖掘结果。因此，闭包（closed）概念被引入效用挖掘中。自然而然，如何从这些高效用闭包项集中还原（derive）所有的高效用项集也是需要解决的问题。 ———— By Suarne

Efficient Mining of a Concise and Lossless Representation of High Utility Itemsets

动机

在频繁项集挖掘领域，已经有学者提出 “闭包（closed）” 概念，旨在得到小体量的挖掘结果。同时，通过闭包集仍然可以还原所有的频繁项集。受该类思路的启发，该文作者提出一种设想：能否在高效用项集挖掘上使得挖掘结果更加简洁？

面临的困难

作者总结出以下四点需要解决的关键问题：

  • 直接照搬频繁挖掘的 closed 处理过程可能会使得挖掘得到的高效用项集降低了原本的效用值，甚至变得没有意义；
  • 在高效用项集挖掘算法上使用 closed 可能并不会达到减小挖掘结果体量的目的；
  • 为了进行 closed 挖掘，可能需要更多的成本，致使新算法表现性能不如原算法；
  • 如何高效地从 closed 结果中恢复原高效用项集信息存在困难

定义

高效用项集相关定义可以参考之前的笔记（HUI-Miner），这里仅对 closed 相关定义进行补充介绍。另，高效用项集使用 HH 表示，闭包项集使用 CC 表示，项集集合用 II 表示

闭包项集

  • 对于所有包含特定项集 XX 的交易项集，可以用一个集合来表示，即 g(X)g(X) = {T1T_1, T2T_2, …\ldots}。那么，XX 在整个数据集中的出现次数（支持度）自然是该集合的大小，即 SC(X)SC(X) = ∣g(X)∣|g(X)|。自然而然，对于其超集的支持度计算可以简化为 SC(X∪Y)SC(X \cup Y) = ∣g(X)∩g(Y)∣|g(X) \cap g(Y)|。

  • 对于项集 XX 的闭包集，定义为 C(X)C(X) = ∩Tj∈g(X)Tj\cap_{T_j \in g(X)}T_j，即存在一个最长的超集 YY，有 X⊆YX \subseteq Y 且 SC(X)SC(X) = SC(Y)SC(Y)，那么可以推理出 SC(X)SC(X) = SC(C(X))SC(C(X)) ↔\leftrightarrow g(X)g(X) = g(C(X))g(C(X))（Ps. 这一点和频繁项集的闭包定义一致，闭包集必然是与其子集同时出现）

  • 对于项集 XX，如果以下两个条件任何一条成立

    1. 不存在项集 YY 有 X⊂YX \subset Y 且 SC(X)SC(X) = SC(Y)SC(Y)，

    2. C(X)C(X) = XX

    那么称 XX 是一个闭包项集（closed itemset）；否则 XX 是一个 非闭包项集（non-closed itemset）

  • 给定一个项集集合 II，对应的闭包项集集合为 fC(I)f_C(I) = {X∣X∈I,¬∃Y∈IX|X \in I, \lnot\exists Y \in I, 有 X⊂YX \subset Y 且 SC(X)SC(X) = SC(Y)SC(Y)}。那么，对于任意的 X∈IX \in I，有 SC(X)SC(X) = max{SC(Y)∣Y∈fC(I)SC(Y)|Y \in f_C(I) 且 X⊆YX \subseteq Y}（Ps. 在频繁闭包项集挖掘算法中，该定义用来从频繁闭包项集中还原所有的频繁项集）同样的，fH(I)f_H(I) = {X∣X∈I,u(X)≥minUtilX | X \in I, u(X) \ge minUtil}

高效用闭包项集

作者提出，判断一个项集是否为闭包有两种方法：

  • 仿照频繁闭包项集的判断做法，当一个高效用项集不存在和它的效用值一样的超集即可认为该项集是闭包的。显然，这个做法有明显的缺陷：1）效用值本身不像频度那样遵循 download closure property，故超集和子集之间的效用值关系没有必然大小联系；2）该方法对缩减挖掘体量没有很大的帮助

  • 采用频繁闭包项集的判断做法，那么就存在两种判断途径：1）先挖掘所有的高效用项集再从中找出闭包项集，即 H′H^\prime = fC(fH(I))f_C(f_H(I))，H′⊆HH^\prime \subseteq H；2）先挖掘所有的闭包项集然后再找出高效用项集，即 C′C^\prime = fH(fC(I))f_H(f_C(I))，C′⊆CC^\prime \subseteq C

那么，这两种方法得到的最终结果是否是一致的，即 H′H^\prime = C′C^\prime？证明如下：

  • 证明 H′⊆C′H^\prime \subseteq C^\prime：取任意项集 XX

    已知X∈H′，H′⊆H，则X∈H；结合¬∃Y∈I，X⊂Y且SC(X)=SC(Y)等价于X∈C；可以推出¬∃Y∈H，X⊂Y且SC(X)=SC(Y)等价于X∈C，反证法：假设当X∉C时，必然∃Y∈I，有X⊂Y和SC(X)=SC(Y)成立，又由于X∈H，且SC(X)=SC(Y)，所以u(Y)>u(X)得Y∈H，汇总可得，X∉C等价于∃Y∈H，有X⊂Y和SC(X)=SC(Y)成立，那么，当¬∃Y∈H，X⊂Y且SC(X)=SC(Y)时，可以推出X∈C，故∀X∈H′，有X∈C′已知 X \in H^\prime，H^\prime \subseteq H，则 X \in H；\\ 结合 \lnot\exists Y \in I，X \subset Y 且 SC(X) = SC(Y) 等价于 X \in C；\\ 可以推出 \lnot\exists Y \in H，X \subset Y 且 SC(X) = SC(Y) 等价于 X \in C，\\ 反证法：假设当 X \not\in C 时，必然 \exists Y \in I，有 X \subset Y 和 SC(X) = SC(Y) 成立，\\ 又由于 X \in H， 且 SC(X) = SC(Y)，所以 u(Y) > u(X) 得 Y \in H，\\ 汇总可得，X \not\in C 等价于 \exists Y \in H，有 X \subset Y 和 SC(X) = SC(Y) 成立，\\ 那么，当 \lnot\exists Y \in H，X \subset Y 且 SC(X) = SC(Y) 时，可以推出 X \in C，\\ 故 \forall X \in H^\prime，有 X \in C^\prime

  • 证明 C′⊆H′C^\prime \subseteq H^\prime：

    已知X∈C′，C⊆C′，则X∈C且X∈H，由于X∈C等价于¬∃Y∈I有X⊂Y且SC(X)=SC(Y)，反证法：假设当∃Y∈H时，由于X⊂Y，Y⊂I且SC(X)=SC(Y)，得X∉C，但实际上，X∈C′∈C，矛盾，故∀X∈C′，有X∈H′已知 X \in C^\prime，C \subseteq C^\prime，则 X \in C 且 X \in H，\\ 由于 X \in C 等价于 \lnot\exists Y \in I 有 X \subset Y 且 SC(X) = SC(Y)，\\ 反证法：假设当 \exists Y \in H 时，由于 X \subset Y，Y \subset I 且 SC(X) = SC(Y)，得 X \not\in C，\\ 但实际上，X \in C^\prime \in C，矛盾，故 \forall X \in C^\prime，有 X \in H^\prime

  • 根据上面的证明，高效用闭包项集集合可以表示为 HCHC = {X∣X∈IX | X \in I, X=C(X)X = C(X), u(X)≥minUtilu(X) \ge minUtil}，其中 HCHC = H′H^\prime = C′C^\prime。同时，非闭包高效用项集（non-closed high utility itemset）成立的条件是 X∈HX \in H 但 X∉CX \not\in C。那么，对于非闭包高效用项集 XX，∃Y∈HC\exists Y \in HC 有 YY = C(X)C(X) 且 u(Y)>u(X)u(Y) > u(X)。（Ps. 证明过程详见论文，该属性其实可以用来作为 X 的上边界剪枝判断，即在数据集中，闭包集 Y 不符合条件的情况下，其子集 X 必然也是不符合条件）

  • 为了确保还原结果的完整性，对于任意项集 XX = {x1x_1, x2x_2, …\ldots, xkx_k}，效用单元组（utility unit array）可以用来记录组成 XX 的所有项在项集 XX 中的效用值信息。表达式为 V(X)V(X) = [v1v_1, v2v_2, …\ldots, vkv_k]，viv_i = V(X,xi)V(X, x_i) = ∑Tj∈g(X)∧xi∈Tju(xi,Tj)\sum_{T_j \in g(X) \land x_i \in T_j}u(x_i, T_j)。同时，u(X)u(X) = ∑vi∈V(X)vi\sum_{v_i \in V(X)}v_i。根据这条公式，可得当 C(X)∉HCC(X) \not\in HC 时，X∉HX \not\in H；反之，当 C(X)∈HCC(X) \in HC 时，u(X)u(X) = ∑xi∈XV(C(X),xi)\sum_{x_i \in X}V(C(X), x_i)（Ps. 也就是说，通过 HC 是可以还原其它高效用项集的信息）

  • 作者命名挖掘目标为 closed+^+ high utility itemset（闭包高效用项集，缩写为 CHUI），不过个人认为，使用 high utility closed itemset（高效用闭包项集） 会更顺口一些

剪枝策略

通用的剪枝策略如 TWU 在这里不做过多介绍，本文仅记录新设计的策略

Removing the Mius of items from Local TU-Tables (RML)

  • 每个项 xix_i 可能会在多个交易项集 TjT_j 中出现，取其中最小的 u(xi,Tj)u(x_i, T_j) 为最小项效用值 miu(xi)miu(x_i)
  • 由于 CHUD 算法采用的是树型结构，所以每一棵构造树（包括子树）都会有一个对应的 table，以空集为根节点的叫做 global TU-Table，以各个项集为根节点的叫做 local TU-Table

由于 CHUD 算法每次对项集进行扩展都是单个单个地增加长度（即 YY = X∪xiX \cup x_i），所以每处理完一个 xix_i 就要将所有对应的交易项集的效用值都减去 miu(xi)miu(x_i)，这样更新后的 local TU-Table 可以用来预估扩展后的项集 YY（Ps. 和剩余效用概念类似，每处理一个扩展的项，该项集能够扩展的效用值其实是在不断减小）

Discarding Candidates with a MAU that is less than the minimum utility threshold (DCM)

  • 每个项 xix_i 可能会在多个交易项集 TjT_j 中出现，取其中最大的 u(xi,Tj)u(x_i, T_j) 为最大项效用值 mau(xi)mau(x_i)
  • 对于项集 XX 的最大效用值为 MAU(X)MAU(X) = SC(X)×∑xi∈Xmau(xi)SC(X) \times \sum_{x_i \in X}mau(x_i)

显然，MAUMAU 是一个很宽松的上边界值，当 MAU(X)MAU(X) 都小于给定的 minUtilminUtil，那么该项集 XX 必然是低效用的

伪代码

本论文提出的新算法是在原 DCI-Closed 算法的基础上进行修改得到的。CHUD 算法本质上属于 two-phase 类算法，即先找出 candidates，然后在这些 candidates 中找出真正的 CHUIs

Main pseudo-code

前两步为准备工作，尽可能过滤掉 unpromising items，缩小后续的检索空间

Main pseudo-code.png

Phase I pseudo-code

找出所有合适的 closed candidates

Phase I pseudo-code.png

Subsume Check pseudo-code

如果为 true，则意味着该项集是一个已经发现的 closed itemset 的子集，无需对 XX 进行扩展

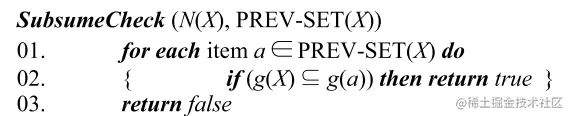
Subsume Check pseudo-code.png

Compute Closure pseudo-code

计算项集 XX 的 C(X)C(X)

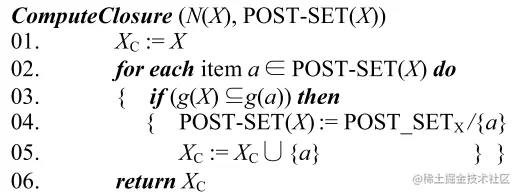
Compute Closure pseudo-code.png

Calculate EstUtility pseudo-code

计算项集 XX 的预估值

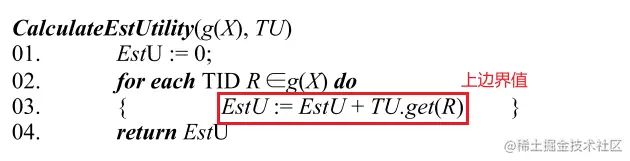
Calculate EstUtility pseudo-code.png

Explore pseudo-code

Explore pseudo-code.png

DAHU pseudo-code

一个自顶向下的方法，从最长的项集（属于 HCHC）开始，每次缩短一个长度，逐个判断

DAHU pseudo-code.png

总结

从论文提供的实验数据来看，CHUI 的数量是远远小于 HUI 的数量（稠密型数据集表现更为明显），而且在运行时间方面，即便加上还原步骤，也不会高出很多。作者详细地分析了在两个阶段的时间和中间结果生成数量，比较有意思的是，该算法采用的基准算法是 UP-Growth，而且在真实数据集 foodmart 上的测试性能并没有想象中那么好，证明该算法实际上性能表现并不是很好。观察实验图的纵轴，运行时间是明显偏长。个人认为在还原高效用项集以及剪枝过程中还有优化的余地，可以加入更有效的判断条件

参考

Efficient Mining of a Concise and Lossless Representation of High Utility Itemsets

avatar
文章
阅读
粉丝