本文从inference问题出发，引出变分推断方法，通过详细的推导和解释讲解了变分推断算法以及其中每个部分的作用，最后介绍了一种最简单的变分推断算法：平均场变分推断。

1. 前言

在贝叶斯体系中，推断(inference)指的是利用已知变量推测未知变量的分布，即我们在已经输入变量$x$后，如何获得未知变量$y$的分布$p(y| x)$。精确推断方法准确地计算$p(y| x)$，该过程往往需要很大的计算开销，现实应用中近似推断更为常用。近似推断的方法往往分为两大类，第一类是采样，常见的是MCMC方法，第二类是使用另一个分布近似$p(y| x)$，典型代表就是变分推断。

变分推断(Variational Inference，下文简称VI)是一大类通过简单分布近似复杂分布、求解推断(inference)问题的方法的统称，具体包括平均场变分推断等算法。首先让我们来看如何得到变分推断优化问题的具体形式。

2. 变分推断

我们假设$x$是观测变量(或者叫证据变量、输入变量)，$z$是隐变量(或者说是我们希望推断的label，在监督学习中通常用$y$表示，但在贝叶斯中，一般会用$z$表示隐变量)，例如在线性回归问题中，$x$是线性回归模型的输入，$z$是线性回归模型的预测值；在图像分类问题中，$x$是图像的像素矩阵，$z$是图像的类别，即label。

贝叶斯模型中，我们的目的是得到后验分布$p(z| x, \phi)$，即我们观测到输入为$x$时，输出变量$z$的概率分布，其中$\phi$为模型参数。精确推断的方法，一般使用贝叶斯公式$p(z| x) = \frac{p(x| z)p(z)}{p(x)} = \frac{p(x| z)p(z)}{\int_z p(x, z) dz}$，然后精确计算每一项的值，得到后验分布，但$p(x)$项涉及到积分的计算，很多时候是很难求解的，所以有了近似推断的方法，更加高效地求解该问题。

VI通过一个简单的分布$q(z| x, \theta)$近似复杂的分布$p(z| x, \phi)$，其中$\theta$是$q$分布的参数，我们希望$q(z| x, \theta)$和$p(z| x, \phi)$的差异越小越好。一般通过反向KL散度来度量这种差异性(什么是反向KL散度，为什么不用一般的KL散度，两者有什么差别等问题在文章最后会解释，这里就先接受这个想法就好)。所以寻找一个与后验分布接近的简单分布的问题就变成了最小化反向KL散度的问题，即：

但因为$p(z| x, \phi)$未知，这个式子是没有办法直接求解的，变分推断通过一系列的变换，然后进行优化。

下面我们直接把积分项$\int_z q(z| x, \theta)f(z)dz$写成等价的期望形式$E_{z\sim q(z| x, \theta)}[f(z)]$，网上的很多推导中，是写成积分或求和形式的，推导过程是完全相同的，但积分和求和形式的推导只针对连续或离散变量中的一种，我选择用期望的形式进行推导，保证推导过程对于连续和离散变量都是成立的。

这里我们定义$\mathcal L= - E_{z\sim q(z| x, \theta)}[-\log \frac{q(z| x, \theta)}{p(z, x| \phi)}]$。注意到第二项$E_{z\sim q(z| x, \theta)}[\log p(x| \phi)]$与$z$无关，所以求期望的结果为$\log p(x| \phi)$，对于优化变量$\theta$是一个常数，不需要优化，之后只考虑第一项的最小化问题，即$\max \mathcal L$，这里的$\mathcal L$被叫做证据下界(Evidence Lower BOund, 即ELBO)，至于为什么叫ELBO会在文章后面解释。因为联合分布$p(z, x| \phi)$也是很难获得的，所以我们还需要进行进一步的转化，才能求解该问题。

转化到这里其实已经可以求解了，式子里的$q(z| x, \theta)$是我们引入的简单的分布，是已知的，$p(x| z, \phi)$是似然函数，也是已知的，$p(z| \phi)$是对于$z$的先验，与$\phi$是无关的，后面直接写成$p(z)$，贝叶斯模型中会假设先验为特定的形式，所以也是已知的，到这里就已经转化为了我们可以计算的形式，推导就已经结束了。但一般会对这个结果进行一个简单的转化，变为直观上更容易理解的形式。

最后一步是根据KL散度的定义直接转化的。推导到这里就结束了，回忆一下整体的流程：VI中使用简单的分布$q(z| x, \theta)$近似复杂分布$p(z| x, \phi)$，所以最小化二者的KL散度，但无法直接求解，所以通过一系列的变换，转化为最大化ELBO的形式，进行求解。所以VI问题就是最大化证据下界，即：

$\max_\theta \mathcal L = \max_\theta E_{z\sim q(z| x, \theta)}[\log p(x| z, \phi)] - KL(q(z, \theta) || p(z))$

文章最开始我们说，VI指的是一大类方法的统称，包含平均场近似等，不同的变分推断算法，其实就是使用不同的方法求解最大化问题。比如平均场近似是假设$q(z)$为平均场分布族，然后使用坐标上升的方法优化，如果假设$q(z)$为其他分布，使用不同的优化方法，就会得到不同的变分推断算法。

直观上理解一下最后的结果：第一项中，$q(z| x, \theta)$是在已知$x$的情况下，使用近似分布获得$z$的过程，可以看做是$x$编码到$z$的过程；$p(x| z, \phi)$是在已知$z$后，获得$x$的过程，可以看做是$z$编码到$x$的过程，第一项直观上衡量了从简单分布$q(z| x, \theta)$中获得一个编码后的结果，多大程度上能够得到编码前的数据$p(x| z, \phi)$。第二项是希望我们的简单分布和真实的$z$的先验分布尽量接近。

接下来我们看一下前面遗留的两个小问题，即为什么使用反向KL散度和为什么$\mathcal L$被称为证据下界。

1. 为什么使用反向KL散度？

首先说一下KL散度(Kullback-Leibler divergence)。KL散度也称为相对熵，是衡量两个分布差异的度量(注意不是距离度量，因为KL散度是非对称的)。$p(x)$是真实分布，$q(x)$是用于近似$p(x)$的近似分布，KL散度衡量了用$q(x)$近似$p(x)$的差异，定义如下：

$KL(p||q) = \sum_x p(x)\log \frac{p(x)}{q(x)}$或$KL(p||q) = \int p(x)\log \frac{p(x)}{q(x)}dx$

注意到这是一般的KL散度的定义，也可以叫做正向KL散度，是$KL(p||q)$，用后面的分布$q$近似前面的分布$p$。而反向KL散度则是$KL(q||p)$，用前面的分布$q$近似后面的分布$p$。那么实际求解时二者有什么区别呢？

首先看正向KL散度：$KL(p||q) = \sum_x p(x)\log \frac{p(x)}{q(x)} = E_{x\sim p(x)}[\log \frac{p(x)}{q(x)}]$。对于任意的$p(x)>0$的点，如果$q(x) \rightarrow 0$，则KL散度会无限大，所以要避免这种情况，近似的结果就会尽量的平摊在整个区域上，就一定不会出现下图中靠上一副图的情况，近似的结果一般是下面一副图的情况。

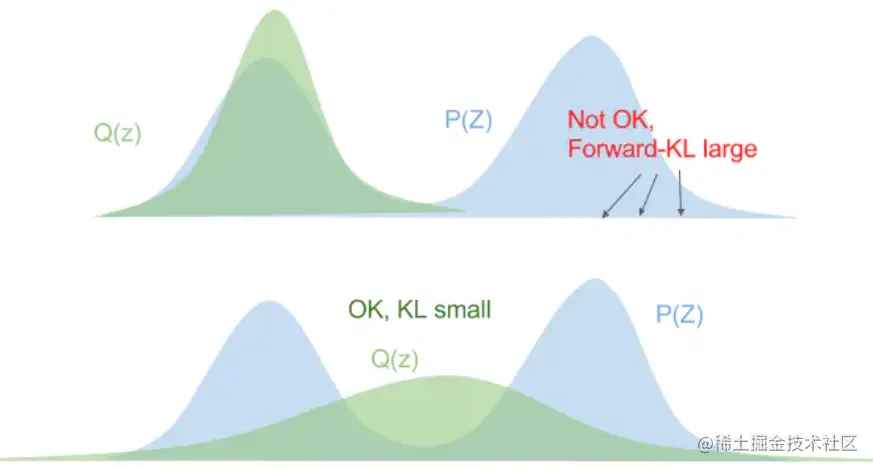
如果是反向KL散度，$KL(q||p) = \sum_x q(x)\log \frac{q(x)}{p(x)} = E_{x\sim q(x)}[\log \frac{q(x)}{p(x)}]$，在$p(x)=0$的地方，为了不让KL散度无限大，$q(x)$一定也为0，就一定不会出现下图中靠上一副图的情况，近似的结果一般是下面一副图的情况。

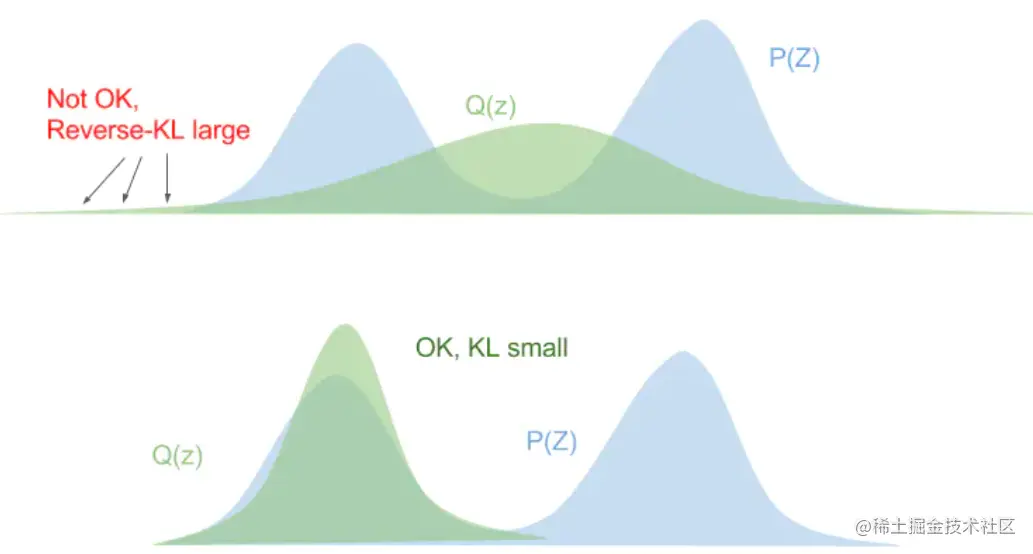
变分推断为什么使用反向KL？(这里是猜的，我也不太清楚)我感觉就是要在多峰时，尽量逼近其中一个峰，而不是尝试逼近所有峰，导致每个位置的近似效果都不好。

2. 为什么公式(2)中的第一项被叫做ELBO

公式(2)的结果为

$KL(q(z| x, \theta)| p(z| x, \phi)) = -\mathcal L + \log p(x| \phi)$

变换形式后：

$\log p(x| \phi) = KL(q(z| x, \theta)| p(z| x, \phi)) + \mathcal L$

公式左边的是关于$x$的函数，右边是$\mathcal L$与KL散度的和，KL散度结果一定大于等于0，所以一定有$\log p(x| \phi) \geq \mathcal L$，在文章开头我们说在贝叶斯模型中，我们称$x$为证据变量，右边可以看做是证据变量的下界，所以叫做证据下界(ELBO)。

3. Mean Field VI 平均场变分推断

平均场变分推断(Mean Field VI, MFVI)中假设$q(z)=\prod_i q(z_i)$为平均场分布族，即可以拆解为多个独立变量函数的乘积。注意这里各个$z_i$之间独立，所以我们可以单独考虑每个变量，这里我们只考虑变量$z_j$，将$q(z)$代入公式(3)的$\mathcal L$中，用$\mathcal L_j$表示只考虑$z_j$的形式。

上面的推导中，第一步到第二步是我们把单独考虑的变量$z_j$与其他的不考虑的变量$z_{-j}$分开，只涉及$z_{-j}$的项可以看做是常量，所以上式中$q(z_{-j}| x, \theta)$和$p(z_{-j}| \phi)$在求期望之后是常量，所以可以直接提取出去。即：

然后我们先考虑第二个对$z_{-j}$的期望，即$E_{z_{-j}\sim q(z_{-j}| x, \theta)}[\log \frac{q(z_j| x, \theta)}{p(x, z_j| z_{-j}, \phi)}] = \log q(z_j| x, \theta) - E_{z_{-j}\sim q(z_{-j}| x, \theta)}[\log p(x, z_j| z_{-j}, \phi)]$，记第二项为$\log \hat{p}(x, z_j| \phi)$。所以：

第一项是KL散度的负数，KL散度大于等于0，当且仅当两个分布相同时，取等号，所以我们要最大化$\mathcal L_j$，就是要让第一项的负KL散度的取最大值$0$，也就是让两个分布相等，即$q(z_j| x, \theta) = \hat{p}(x, z_j | \phi)$，所以我们的优化算法就是要迭代地优化$z_j, j=1, \dots, n$，使得每一个分布相等，就引出了坐标上升的方法对平均场变分推断进行优化：

4. 总结

到这里差不多就结束了，变分推断还有很多其他的内容，比如平均场变分推断中，假设各个变量独立，这个假设过强，很多时候不满足，所以有了考虑变量之间关系的变分推断。以及深度学习中的变分自编码器，很多很多的内容，留着之后再写吧。

最后，欢迎关注我的公众号：炼丹攻略。(尽量)每周更新人工智能方面的知识。