一起养成写作习惯！这是我参与「掘金日新计划 · 4 月更文挑战」的第11天，点击查看活动详情。

旋转的轴角描述法

选定一个旋转轴

注意，这个旋转轴必须是经过坐标系的原点$(0,0,0)$，方向可以随意, 长度不影响结果。

绕轴旋转

我们一般说的旋转的正方向就是指逆时针方向，也就是说，不特别指定的话，旋转就是指逆时针旋转。

一个例子

比如说，我们有一个向量$(1,0,0)$, 绕着一个轴$(0,1,0)$, 旋转90°。

我们可以看出这个轴就是Y轴。

在坐标系是右手坐标系的情况下：

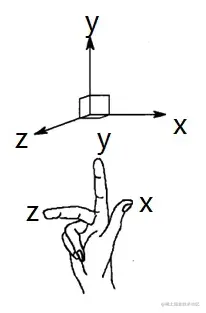
我们可以得知，旋转后的坐标是$(0,-1,0)$。

轴角描述的四个要素

我们可以看出，规定一个旋转轴需要三个数字，规定一个旋转角度需要一个数字，这一共就是四个数字：

• 旋转轴：$(x,y,z)$
• 旋转角度：$α$

难不成这就是大名鼎鼎的四元数(quaternion)。

当然，不是！不急，下面慢慢讲。

四元数概念

定义

有任意四个数，$a,b,c,d ∈ R$, 那么

• $q = a + b i + c j + d k$ 则是四元数

其中， $i^2 = j^2 = k^2 = ijk= -1$,

i、j、k 是虚数单位。

四元数加减法

加减法很简单，四个数对应相加减即可：

令
$q_1 = a_1 + b_1 i + c_1 j + d_1 k$
$q_2 = a_2 + b_2 i + c_2 j + d_2 k$
则
$q_1+q_2 = (a_1 + a_2) + (b_1 + b_2)i + (c_1+c_2) j + (d_1+d_2) k$ $q_1-q_2 = (a_1 - a_2) + (b_1 - b_2)i + (c_1-c_2) j + (d_1-d_2) k$

四元数数乘

所谓数乘，就是一个数字乘以一个四元数：

现有$m$和一个四元数$q = a + b i + c j + d k$
则 $mq = ma + mb i + mc j + md k$

两个四元数相乘

令
$q_1 = a_1 + b_1 i + c_1 j + d_1 k$
$q_2 = a_2 + b_2 i + c_2 j + d_2 k$

$q_1 q_2$ = ?

按照小学学的知识可以一步一步算出来：

$q_1 q_2 =$
$(a_1a_2 - b_1 b_2 - c_1 c_2 - d_1 d_2)+$
$(b_1a_2 + a_1 b_2 - d_1 c_2 + c_1 d_2)i+$
$(c_1 a_2 + d_1 b_2 + a_1 c_2 - b_1 d_2)j+$
$(d_1 a_2 - c_1 b_2 + b_1 c_2 + a_1 d_2)k$

注意， 四元数相乘，不满足交换律也就是说

$q_1 q_2 ≠ q_2 q_1$

一个四元数的逆

假设 $q_1 q_2 = 1$, 那么 $q_1 和 q_2$互逆，并有以下记法：

$q_1 的逆是 q_1^{-1}$。

一个四元数的共轭

定义：$q = a + b i + c j + d k$ 的共轭是
$a - b i - c j - d k$

并有如下记法：
$q的共轭记作：q^*$

四元数代表旋转

先把轴角描述法的要素列出来：

$旋转轴：(u,v,w) 、 旋转角度: α、$ 还有一个初始向量$(x,y,z)$

我们利用上面这些要素，来构造两个四元数：

$v = xi+yj+zk$
$q = cos({1 \over 2}α ) + sin({1 \over 2}α )ui + sin({1 \over 2}α )vj+ sin({1 \over 2}α )wk$

那么做如下的计算：

$r = qvq^* = qvq^{-1}$

此时 r 是一个四元数，并且 只有ijk三项有值，第一项为0.

我们把ijk三项的系数拿出来$(r_i, r_j, r_k)$, 此时这个新的向量就是 初始向量$(x,y,z)$ 绕着旋转轴：(u,v,w)逆时针旋转了 $α$之后得到的。