0.论文信息

图例1.可以看出在Stable Learning模型相较于传统模型学习的优势

1.文章提出的背景

传统深度学习模型在源域与目标域不同时（即Out-Of-Distribution问题）学习效率不太行，是因为在分布中具有虚假的相关性，比如上图中的狗和水，其实判定狗并不需要水，但是因为源域数据的分布，模型会反映出这个虚假的相关性。
现有的Domain Generalization解决问题的核心是将类别划分为多个分布域，使得真正相关的特征在不同域中都有共性体现，而虚假的相关特征在不同域中千差万别。但是这种方法的弊端也显而易见，很多方法仍然建立在隐含地假设潜在域是平衡的这一基础之上。
假定训练数据的分布是未知的并且不隐含假设潜在域是平衡的，想要很好地解决这一问题时，存在两点挑战 ：
- 特征之间的复杂的非线性依赖性比线性难以测量和消除
- 我们在全局样本加权策略中需要在深层模型中储存和计算，这将需要大量的成本并不容易实现
随后，给出了对应的解决思路：
- 针对第一个问题，提出了一种基于随机傅里叶特征的新型非线性特征去相关方法，具有线性计算复杂性。
- 针对第二个问题，提出了一个通过迭代节省和重新加载模型的特征和权重来感知和清除全局相关性的方法。

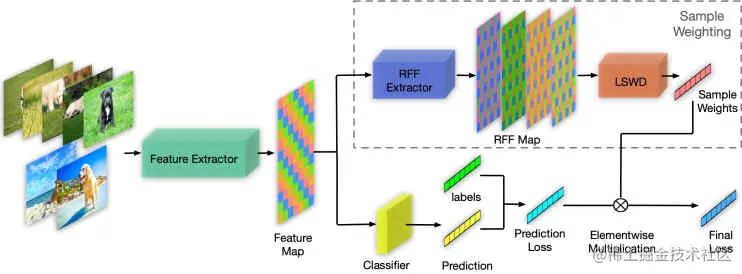
图例2.Stable Learning的整体网络结构

传统的希尔伯特-施密特独立标准（HSIC）需要进行矩阵的平方运算，但是随着batch size的增大开销将大幅上涨，所以在大型数据训练的模型中不可实用。

实际上，Frobenius范数对应于欧几里德空间的HSIC范数，因此独立的测试统计可以基于Frobenius范数。

所以局部协方差可以采用以下的表达形式

\hat\Sigma_{AB}=\frac{1}{n-1}\sum_{i=1}^n[({\rm \bold u}(A_i)-\frac{1}{n}\sum_{j=1}^{n}{\rm \bold u}(A_j))^T\cdot({\rm \bold v}(B_i)-\frac{1}{n}\sum_{j=1}^{n}{\rm \bold v}(B_j))]\\ {\rm \bold u}(A)=(u_1(A),u_2(A),...,u_{n_A}(A)),\ u_j(A)\in \mathcal{H}_{RFF} \\ {\rm \bold v}(B)=(v_1(B),v_2(B),...,v_{n_B}(B)),\ v_j(B)\in \mathcal{H}_{RFF} \\ \mathcal{H}_{RFF} = \{h:x\rightarrow\sqrt{2}\cos{\omega x+\phi}\ |\ \omega\sim N(0,1),\phi\sim {\rm \bold Uniform}(0,2\pi)\}\\ I_{AB}=\parallel \hat\Sigma_{AB}\parallel_F^2

更进一步地，可以使用可学习的权重来更好地去除相关性，引入权重 ${\rm \bold w}$

\hat\Sigma_{AB;{\rm \bold w}}=\frac{1}{n-1}\sum_{i=1}^n[({\rm \bold w}_i{\rm \bold u}(A_i)-\frac{1}{n}\sum_{j=1}^{n}{\rm \bold w}_j{\rm \bold u}(A_j))^T\cdot({\rm \bold w}_i{\rm \bold v}(B_i)-\frac{1}{n}\sum_{j=1}^{n}{\rm \bold w}_j{\rm \bold v}(B_j))]

对于两个不同的特征 ${\rm \bold Z}_{:,i}$ 与 ${\rm \bold Z}_{:,j}$ ， ${\rm \bold w}$ 对应优化即为

{\rm \bold w}*=\argmin_{{\rm \bold w}\in\Delta_n}\sum_{1\le i<j\le m_Z}\parallel \hat\Sigma_{{\rm \bold Z}_{:,i}{\rm \bold Z}_{:,j};{\rm \bold w}}\parallel_F^2\\ \Delta_n=\{{\rm \bold w}\in\mathbb{R}_+^n\ |\ \sum_{i=1}^n\omega_i=n\}

对应的表示函数 $f$ 、预测函数 $g$ 有如下关系式

{\rm \bold w}^{(0)}=(1,1,...,1)^T\\ {\rm \bold Z}^{(t+1)}=f^{(t+1)}({\rm \bold X})\\ f^{(t+1)},g^{(t+1)}=\argmin_{f,g}\sum_{i=1}^nw_i^{(t)}L(g(f({\rm \bold X}_i)),y_i)\\ {\rm \bold w}^{(t+1)}=\argmin_{{\rm \bold w}\in\Delta_n}\sum_{1\le i<j\le m_Z}\parallel \hat\Sigma_{{\rm \bold Z}_{:,i}^{(t+1)}{\rm \bold Z}_{:,j}^{(t+1)};{\rm \bold w}}\parallel_F^2

对于每个batch，规定 ${\bold Z}_O$ 与 ${\bold w}_O$ 如下，其中 ${\bold Z}_{G_i},{\bold w}_{G_i}$ 表示在每批次训练后更新的全局变量，而 ${\bold Z}_{L}$ 与 ${\bold w}_{L}$ 则代表本地存储的全局变量。

{\bold Z}_O={\rm Concat}({\bold Z}_{G_1},{\bold Z}_{G_2},...,{\bold Z}_{G_k},{\bold Z}_{L})\\ {\bold w}_O={\rm Concat}({\bold w}_{G_1},{\bold w}_{G_2},...,{\bold w}_{G_k},{\bold w}_{L})

并使用如下的更新规则

{\bold Z}_{G_i}'=\alpha_i{\bold Z}_{G_i}+(1-\alpha_i){\bold Z}_L\\ {\bold w}_{G_i}'=\alpha_i{\bold w}_{G_i}+(1-\alpha_i){\bold w}_L

图例3.使用StableNet训练的更多场景及其对比效果

为了解决问题提出StableNet......较好地解决了问题

在这篇文章中，通过使用改进的Frobenius范数来衡量相关性并尽量去除掉虚假的相关性。感觉在相关性背后的深层逻辑其实还是因果性，但是使用相关性的处理要比因果性方便很多且行之有效，所以使用相关对于因果进行简化也不失为一种好的思路。