双目视觉（一）双目立体视觉原理打炮的时候用大拇指测距就是双目立体视觉的现实应用，通过交替闭上左右眼就可以估测出目标点距离

相机成像原理

下图就是相机的成像原理，图像中的被摄点 $(x, y)$ ，在现实中的位置可以是该点和相机连成的直线上的任意位置。

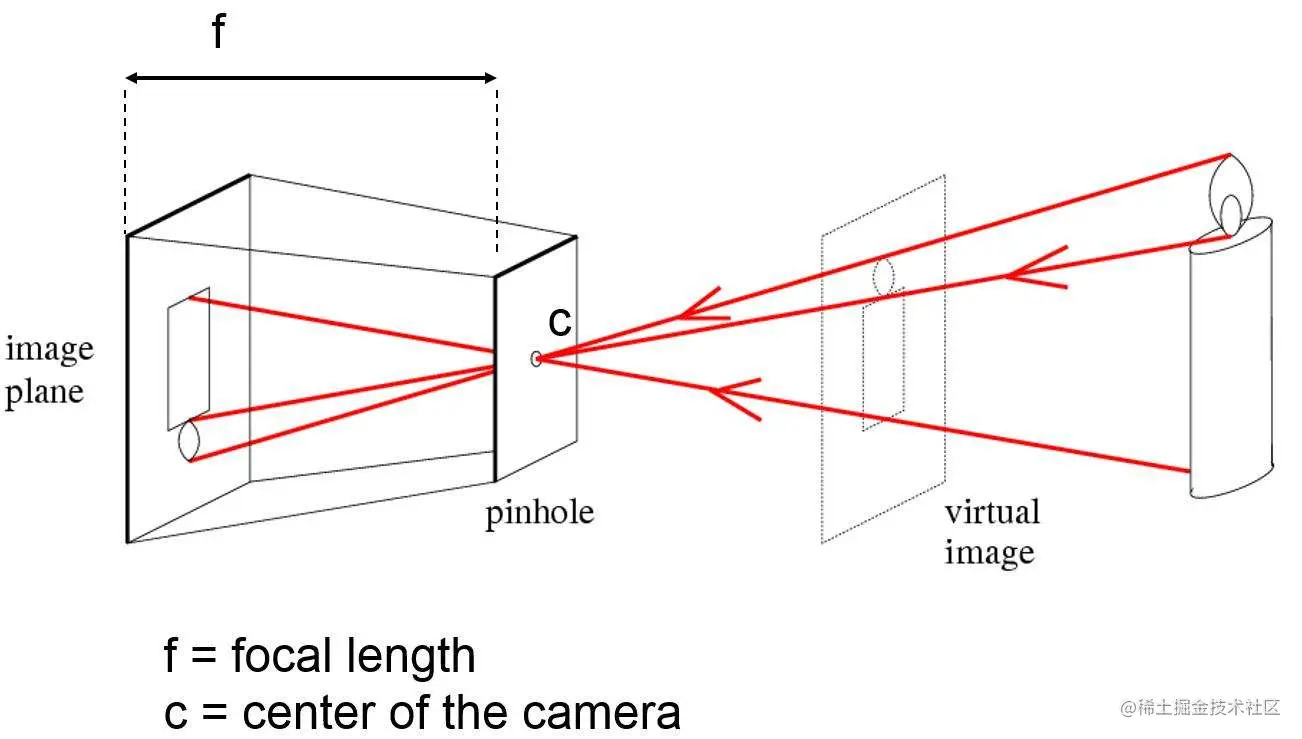
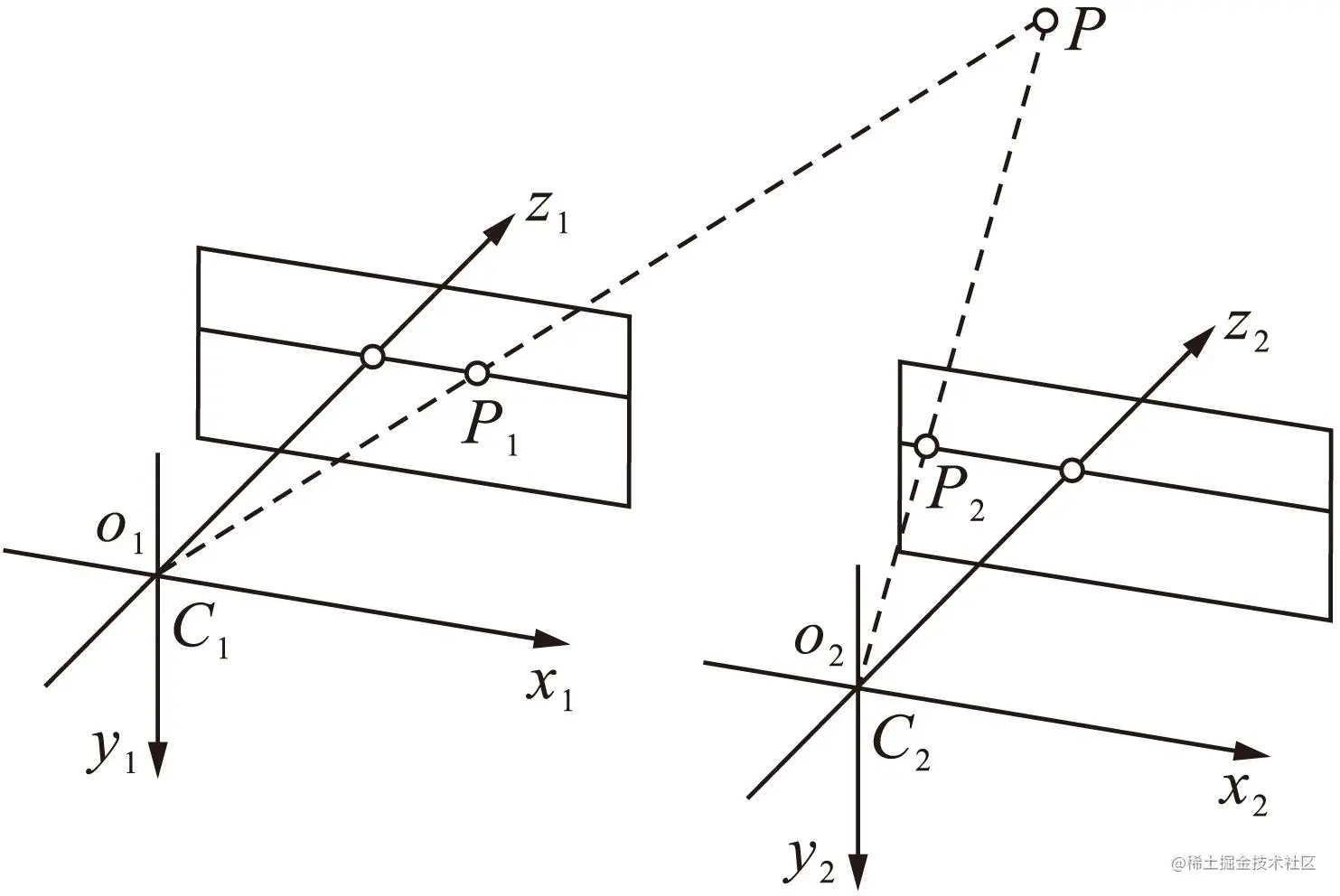
如果要确定被摄点在现实中的位置，需要两个相机从不同角度同时拍摄，如下图所示， $(C_1, P_1)、(C_2, P_2)$ 两条直线相交于 $P$ 点，即被摄点在现实中的位置。

上图中的画出的两个坐标系称为相机坐标系，以相机在现实中的位置 $C_1、C_2$ 为原点。

$P$ 所处的坐标系称为世界坐标系，原点位置可以任选，例如可以将右相机坐标系当作世界坐标系，以 $C_2$ 为原点。

上图中画出的 $P_1、P_2$ 所在的平面上的坐标系称为投影坐标系，以物理尺寸为单位；拍摄得到的图像上的坐标系称为图像坐标系，以像素为单位。

图像其实就是数组，数组中的元素就是像素，彩色图用3个整型值描述1个像素，灰度图用1个整型值描述1个像素。

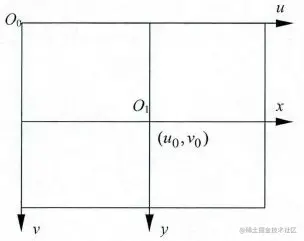
图中 $O_0$ 为图像坐标系，原点为图像左上角像素位置； $O_1$ 为投影坐标系，原点为像主点 $(u_0, v_0)$ 位置。

像主点就是相机坐标系原点到成像平面的垂点，即图二中 $z$ 轴与成像平面的交点。

通过被摄点的两个图像坐标得到被摄点的世界坐标，就是立体视觉。

设单个像素对应到相机的感光平面上的物理尺寸为 $(d_x, d_y)$ ，像主点在图像坐标系中的坐标为 $(u_0, v_0)$ ，则有投影坐标 $(x, y)$ 和图像坐标 $(u, v)$ 间的转换关系如下：

u - u_0 = \frac{x}{d_x}

v - v_0 = \frac{y}{d_y}

算法中的数学运算一般使用矩阵运算，因此上面的公式等价于：

\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}

由于制造工艺的偏差， $d_x ≠ d_y$ ，像素并不是正方形，而是平行四边形，这里先假设像素是个矩形，后面会提到倾斜因子的问题。

如下图所示， $O1$ 为投影坐标系， $O$ 为相机坐标系，设 $P$ 点在投影坐标系中的坐标为 $(x, y)$ ，则 $P$ 点在相机坐标系中的坐标为 $(x, y, f)$ ， $f$ 表示焦距，即 $O$ 点到 $O1$ 点的距离。

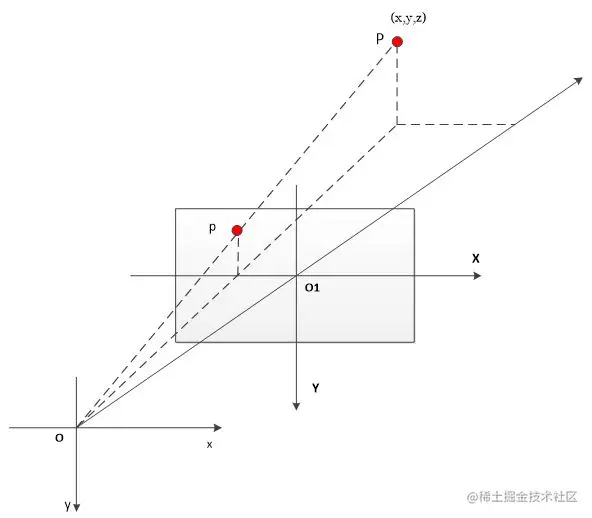
由相似三角形原理，可得投影坐标 $(x, y)$ 和相机坐标 $(X_c, Y_c, Z_c)$ 间的转换关系如下：

\frac{x}{X_c} = \frac{y}{Y_c} = \frac{f}{Z_c}

同样的，上面的公式等价于：

\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{f}{Z_c} & 0 & 0 \\ 0 & \frac{f}{Z_c} & 0 \\ 0 & 0 & \frac{1}{Z_c} \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix}

这里 $x = Z_x、y = Z_y、f = Z_c$ ，但这里没有在公式中把 $f$ 约掉，后面会说明。

上文假设了世界坐标系和左相机坐标系一致，但在相机标定时需要以标定板的角点为世界坐标系原点。3维坐标的转换可以通过旋转和平移实现。

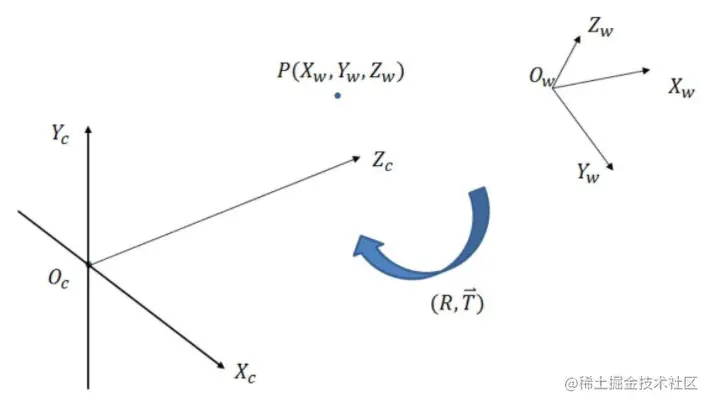
其中 $R_{3\times3}$ 为旋转矩阵， $T_{3\times1}$ 为平移矩阵，相机坐标 $(X_c, Y_c, Z_c)$ 和世界坐标 $(X_w, Y_w, Z_w)$ 间的转换关系如下：

\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix} = R_{3\times3} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix} + T_{3\times1} = \begin{bmatrix} R_{3\times3} & T_{3\times1} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ \end{bmatrix}

坐标转换中涉及的 $(d_x, d_y)、(u_0, v_0)、f、R、T$ 这些都是相机的参数，可以通过相机标定获得。

由图像 ⇌ 投影、投影 ⇌ 相机两个坐标转换关系，可以得出图像 ⇌ 相机的坐标转换关系如下：

\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \frac{1}{Z_c} \begin{bmatrix} \frac{f}{d_x} & 0 & u_0 \\ 0 & \frac{f}{d_y} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ \end{bmatrix}

其中， $\frac{f}{d_x}、\frac{f}{d_y}$ 的含义是将以物理尺寸为单位的焦距 $f$ ，转换为以像素为单位的焦距值，记 $f_x = \frac{f}{d_x}、f_y = \frac{f}{d_y}$ 。

补上上面提出的 $f = Z_c$ 为什么不约掉 $f$ 的问题，因为标定相机得出的是 $f_x、f_y$ ，不约掉更加方便计算。

K = \begin{bmatrix} f_x & s & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix}

称呼矩阵 $K$ 为相机的内参数，内参数是固定不变的。

补充上面提出的像素为平行四边形的问题，这里的 $s$ 表示像素纵向边界相比于 $y$ 轴的倾斜因子，用于辅助计算。

相机 ⇌ 世界坐标转换关系中的 $R、T$ 矩阵就是相机的外参数，表示世界坐标系到相机坐标系的旋转和平移矩阵，在立体视觉中，我们一般不关心世界坐标系到两个相机坐标的转换关系，而是关心两个相机坐标系间的转换关系。

相机标定能获得左相机的 $R_1、T_1$ 和右相机的 $R_2、T_2$ ，有了这些就可以计算左相机坐标系到右相机坐标系的旋转和平移矩阵 $R、T$ （这里是以右相机为主视相机，当然也可以反过来）。

通过被摄点的两个图像坐标得到被摄点的世界坐标，就是立体视觉。

结合上文的3个转换关系，设 $λ = Z_c$ 我们可以得出图像 ⇌ 世界的坐标转换关系如下：

λ\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = K_{3\times3} \begin{bmatrix} R_{3\times3} & T_{3\times1} \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}

设 $P = \begin{bmatrix}R_{3\times3} & T_{3\times1}\end{bmatrix}$ ，称为投影矩阵，也就是相机内参和外参的结合体。

λ\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = P_{3\times4} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}

上面的方程是单个相机的，最开始已经提过了，方程的解集是一条直线，两个相机对应两个方程，解集是一个点。

能求出被摄点的世界坐标，也就能得出被摄点到相机的距离、两个被摄点之间的距离等。写这篇文章的原因是因为自己的毕设需要，之前并没有接触过机器视觉方面的知识，如果有不专业或错误的地方万望指出。

本文并没有提到相机标定和具体代码如何实现，这些会后面再写文章来讲。