上一篇文章中我们描述了SPJG的物化视图的改写，其中的J只能是inner join。本文中我们将描述outer join的物化视图的改写。与inner join不同，我们不能将其简单地视为笛卡尔积的问题，而是需要一些复杂的变换。

定义

这里我们对后面要用到的符号和定义做一些总结。

$null-rejecting$: 当一个selection条件$p$所引用的任意列是$null$，则$p$肯定不为$true$，这是我们说$p$是$null-rejecting$。

$null(T)$: 当某一行在表$T$的列上全是$null$，则$null(T)$为真。比如$T_1 \rtimes T_2$的结果中，当$T_1$中的某行$t_1$在$T_2$中没有找到任何匹配的行时，我们需要对$T_2$所对应的列填充$null$，那么对这一行$null(T_2)$ 就是 $true$。如果 $\Tau = \{T_1, T_2, \ldots, T_n\}$，那么$null(\Tau) = null(T_1) \land null(T_2) \ldots null(T_n)$，$\overline{null}(\Tau) = \text{\textasciitilde} null(T_1) \land \text{\textasciitilde}null(T_2) \ldots \land \text{\textasciitilde}null(T_n)$。

$\uplus (outer\ union)$: 假设表$T_1$的schema是$S_1$，表$T_2$的schema是$S_2$，那么$T_1 \uplus T_2$首先null extend$T_1$和$T_2$是他们的schema是$S_1 \cup S_2$，然后做一个union all的操作。例如，假设$T_1$的schema和数据如下：

int	float
1	1.1
2	2.2

$T_2$的schema和数据如下：

double	int
3.3	3
4.4	4

那么$T_1 \uplus T_2$的schema和数据如下：

int	float	double	int
1	1.1	null	null
2	2.2	null	null
null	null	3.3	3
null	null	4.4	4

$subsume$: $t_1$ $subsume$ $t_2$指的是$t_1$和$t_2$有相同的schema，$t_1$中的$null$少于$t_2$，并且$t_2$中的某个值不是$null$，则$t_1$中对应的值也不是$null$；而对于$t_2$中的非$null$值，$t_1$中包含相同的值。例如，$t_1$是$（1,2,null)$，$t_2$是$(null, 2, null)$，则我们认为$t_1\ subsume\ t_2$。

$T\downarrow$: 如果表$T$中的某个tuple被另一个tuple $subsume$了，则去除所有这样的tuple得到的结果。

$T_1 \oplus T_2(minimum\ union): T_1 \oplus T_2 = (T_1 \uplus T_2)\downarrow$

$Q_1 \subset_s Q_2(subsume\ contained)$: $Q_1 \subset_s Q_2\ if\ \forall t_1 \in Q_1, \exists t_2 \in Q_2, t_1 = t_2\ or\ t_2\ subsumes\ t_1$

Join-Disjunctive Form

这里我们首先介绍几个变换规则：

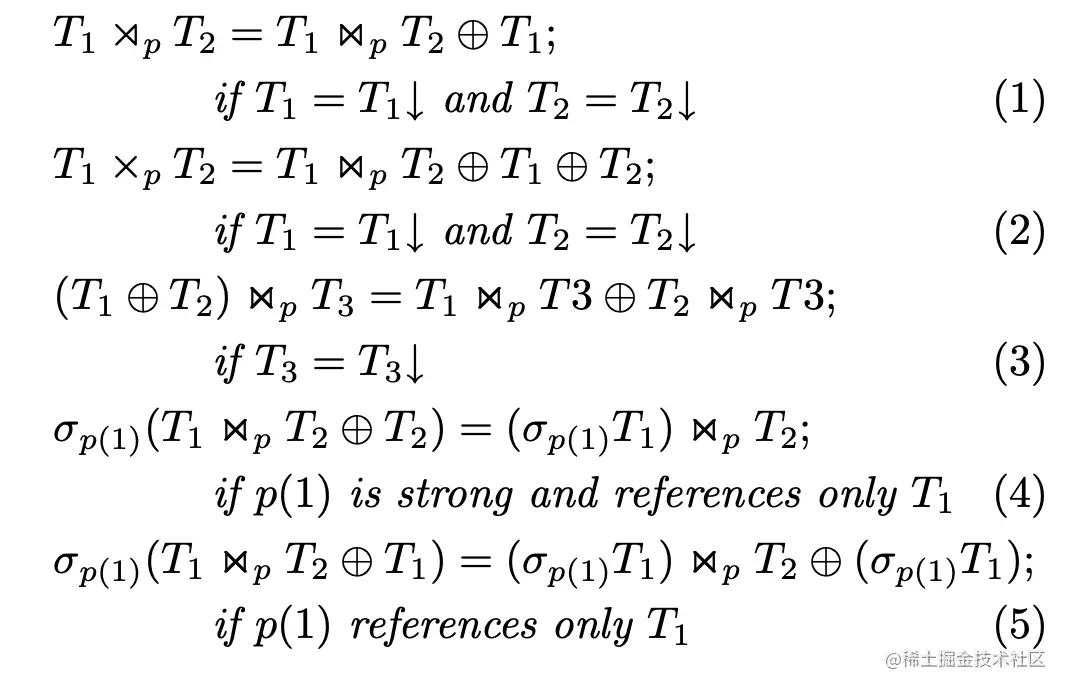
任何一个SPOJ的表达式，如果所有的表都满足$T_i = T_i\downarrow$，并且所有的selection条件都是$null-rejecting$的情况下，我们可以将其转化成join-disjunctive 的形式，即：

其中$\Upsilon_i = T_{i1} \bowtie T_{i2} \ldots \bowtie T_{in}$。这里我们将每个$\delta_{pi}(\Upsilon_i)$称作一个term，我们可以看到每个term就是一个SPJ Query。举个例子，我们可以将如下的SPOJ的Query转化成join-disjunctive form：

转化之后的结果是：

从MV里计算Query

MV是否包含Query的所有行

为了从MV里计算Query的结果，我们首先要知道MV是否包含Query所需要的所有行。这里我们直接使用论文里证明过的一个定理：

假设$Q_1$和$Q_2$是2个SPOJ的Query，$Q_1^{'}$和$Q_2^{'}$分别是对应的join-disjunctive form。那么当且仅当$\forall \delta_{pi1}(\Upsilon_{i1}), \exists \delta_{pj2}(\Upsilon_{j2}) \in Q_2^{'}, 使得 \delta_{pi1}(\Upsilon_{i1}) \subset \delta_{pj2}(\Upsilon_{j2})$时，我们有$Q_1 \subset_{s} Q_2$

从上述定理可以看出，要检测$Q_2$是否包含$Q_1$，只需要检查$Q_1^{'}$的每个term是否被包含在$Q_2^{'}$中。定理的证明比较复杂，这里我们不做详述。举一个例子来说明。假设

从MV中恢复Query所需要的行

假设$Q_1$被证明包含在$Q_2$中，那么我们要计算出$Q_1$的值，只需要计算出$Q_2$中对应的term的值，并且按照第一篇文章中的算法进行过滤，然后执行$\oplus$即可得到$Q_1$的值。

那么对于一个SPOJ的MV，如何恢复每个term的值呢？遗憾的是不是所有的term值都可以恢复的，我们这里讨论2中情况：

1. 当这个term的每一行都包含一个unique key的时候，我们可以通过选出不在term上null-extend的值，然后做一个去重操作即可计算出来。假设$\delta_{P}(\Upsilon)$是我们需要找出的term，并且该term的每一行都以一个unqie key，则

   $$\delta_{P}(\Upsilon) = \sigma(\pi_{\Upsilon .*}\delta_{\overline{null}(\Upsilon)}V)$$

2. 当这个term中的每一行不包含unique key的时候，如果对于该query中的其他term，存在有如下关系时，我们仍然可以计算出来。假设需要计算的term是$\delta_{P_i}(\Upsilon_i)$，对于该query中其他的term$\delta_{P_j}(\Upsilon_j)$，我们都满足2中条件之一： a. $\{T_{i1}, T_{i2}, \ldots, T_{in}\} \not\subset \{T_{j1}, T_{j2}, \ldots, T_{jn}\}\ and\newline \{T_{j1}, T_{j2}, \ldots, T_{jn}\} \not\subset \{T_{i1}, T_{i2}, \ldots, T_{in}\}$ b. $\{T_{i1}, T_{i2}, \ldots, T_{in}\} \subset \{T_{j1}, T_{j2}, \ldots, T_{jn}\}$，但是$\{T_{i1}, T_{i2}, \ldots, T_{in}\}$ 是被通过一些列的cardinality reserving的join跟剩余的table join起来。

   当满足上述条件之后，我们发现$\delta_{P_i}(\Upsilon_i)$在MV中的duplication factor是正确的，如此我们通过如下的操作即可恢复出$\delta_{P_i}(\Upsilon_i)$的值：

   $$\delta_{P_i}(\Upsilon_i)= \pi_{\Upsilon_i.*}\delta_{\overline{null}(\Upsilon_i)}V$$

当我们需要计算多个term的时候，需要注意避免多次扫描MV，而是通过把$\oplus$转换成$union$来做。

SPOJG的改写

SPOJG的改写与上一篇文章中提到的SPJG的改写基本相同，但是在恢复tuple的时候我们要注意SPOJ的特殊部分，因此每个tuple的duplication factor应该相同，这里就不在赘述。

参考文献

1. View Matching for Outer-Join Views, 2005
2. Outerjoins as disjunctions, 1994