隐马尔可夫模型（HMM）

---

1. 隐马尔可夫模型定义

隐马尔可夫模型，根据字面意思。首先它一定存在马尔可夫链，即服从马尔可夫性质：无记忆性。也就是说，某一时刻的状态只受前一时刻影响，而与更早的状态无关。其次，“隐”的意义是，对某一问题，存在一个隐藏的状态序列来指导现实，但是无法形象化显示，故被称为隐状态。

下面介绍给出HMM的基本要素：状态集，观测集，隐状态序列，观测集序列，初始概率分布，状态转移概率，发射概率。

状态集Q和观测集V

所有可能的隐藏状态集Q，所有可能的观察值集V，其中$n$是可能的状态数，$m$是可能的观察数： $Q={q_1,q_2,,,q_n}, V={v_1,v_2,,,v_m}$

隐状态序列$I$和观测集序列$O$

假设$I$是长度为$T$的隐状态序列，$O$是其对应的观测值序列： $I=\{i_1,i_2,,,i_T\}, O=\{o_1,o_2,,,o_T\}$

初始概率分布$\pi$

$\pi=(\pi_i)$ 其中表示在t时刻，$\pi_i=p(i_1=q_i)$，表示在t=1时刻隐状态为$q_i$的概率。)$

隐状态转移概率A

$A=[a_{ij}]_{n*m}$ 其中，$a_{ij}=p(i_t=q_j|i_{t-1}=q_i)$表示t-1时刻的状态$q_i$转移到t时刻状态$q_j$的概率。

发射概率B

发射概率表示由隐状态得到观测状态的概率， $B=[b_j(k)]_{n*m} \\ b_j(k)=p(o_t=v_k|i_t=q_j)$ 其中，$b_j(k)$表示在状态$q_j$发射得到$v_k$的概率。

---

2. HMM可以解决的三个问题

1. 概率计算，给定一个确定的HMM模型（即参数$\lambda = \{A,B,\pi\}$确定）和观测序列$O$，求在该模型参数下观测序列的输出概率。
2. 学习问题，已知观测序列$O$，估计模型参数$\lambda = \{A,B,\pi\}$，使得在该模型下观测序列的概率最大。
3. 预测问题，已知模型的参数$\lambda = \{A,B,\pi\}$和观测序列$O$，求解一组使得观测序列概率最大的隐状态序列。对应NLP中的任务有：分词，词性标注，

---

3. HMM解决三个问题的具体算法

对应上面的三个问题，分别有经典的算法：

1.概率计算（观察序列的概率）

(1) 暴力算法 直接的算法就是计算所有可能的概率，即： $P(O|\lambda) = p(O,I|\lambda) = p(O|I,\lambda)p(I|\lambda)$

其中$I={i_1,i_2,,,i_T}$是隐序列，每个时刻都有N种状态，由于隐状态与观测序列无关，所以其概率为： $p(I|\lambda) = \pi_{i_1}a_{i_1i_2}a_{i_2i_3}...a_{i_{T-1}i_T}, i=1,2,3,....T$

在参数和隐状态都确定的情况下，产生观测序列$O$的概率就是发射概率的乘积，即： $p(O|I,\lambda)=b_{i_1(o_1)}b_{i_2(o_2)}...b_{i_T(o_T)}$

最终的结果就是上面两者的乘积： $P(O|\lambda)=\pi_{i_1}b_{i_1(o_1)}a_{i_1i_2}b_{i_2(o_2)}...a_{i_{T-1}i_T}b_{i_T(o_T)}，i=1,2,3,....T$

算法的复杂度是$TN^T$。

(2) 前向算法 在给定模型参数和观测序列$O=\{o_1,o_2,..o_T\}$的下，$a_t(i)$表示t时刻$a_t=i$的前向概率： $a_t(i)=p(o_1,o_2,...o_t,i_t=q_i|\lambda)$ 由前向递推关系，$a_t(i)$等于t-1时刻所有可能的状态转移到当前状态$o_t$的概率之和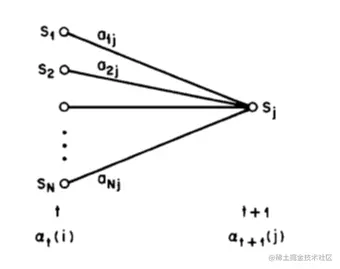： 详细来说，在计算t+1时刻概率时，前向算法如下：

1. 初始值定义： $a_1(i)=\pi_{i1}b_i(o_1),i=1,..n$
2. 递推公示(上图中i,j与公式中不对应)： $a_{t+1}(i)=[\sum_{j=1}^{n}{a_t(j)a_{ji}}]b_{ji}$
3. 在T时刻求和 $P(O|\lambda)=\sum_{i=1}^{n}{a_T(i)}$

(3) 后向算法 与前向算法相似，在给定观测序列$O=\{o_1,o_2,..o_T\}$下，$\beta_t(i)$表示t时刻$a_t=i$的后向概率： $\beta_t(i)=p(o_{t+1},o_{t+2},...o_T,i_t=q_i|\lambda)$

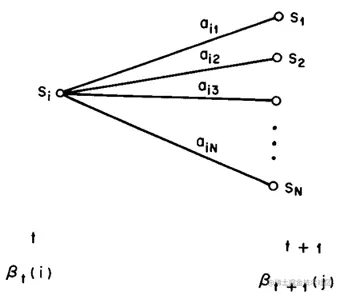
根据后向递推关系，$\beta_t(i)$等于所有可能的t+1时刻状态转移到当前状态（同时t+1时刻发射出观测值$o_{t+1}$）的概率之和。因此，后向算法计算如下：

1. 赋初值 $\beta_T(i)=1, i=1,2..n$
2. 反向递推公式： $\beta_t(i)=\sum_{j=1}^n{a_{ij}b_{j(o_{t+1})}}\beta_{t+1}(j)$
3. 在0时刻求和 $p(O|\lambda)=\sum_{i=1}^n{\pi_{i1}b_{j(o_1)}\beta_1(i)}$

前向和后向算法，都是利用序列之间的递推关系，以及动态规划的算法实现。

【参考】 1. 前向算法和后向算法代码实现

2.参数估计

一般来说，隐马尔可夫的参数估计问题有两种：有监督和无监督。有监督意味着，在训练过程中，已知观测序列和隐序列，这种参数估计可以直接使用最大似然估计。无监督意味着，训练集只给了观测序列，这种情况需要使用EM算法，先假设参数，通过期望最大化来获得隐状态序列，根据隐状态序列来更新参数，不断迭直至收敛。

1. 有监督（最大似然估计）
2. 无监督（Baum-Welch）

3.状态预测

隐状态的转移其实是一个有向无环图，而状态预测问题就是在这个有向无环图中寻找最短路径，维特比算法就是一种利用动态规划算法在这种篱笆网络中寻找最短路径的算法。

首先引入$\sigma_t(i)$的概念，它表示从t=1时刻到t时刻观测状态为i的最优路径的概率值。则： $\sigma_t(i)=\max_{i_1,i_2..i_{t-1}}{(i_t=i,i_{t-1}..i_1,o_t..o_1|\lambda)},i=1,2...n$ 递推得到t+1时刻(t+1时刻的观测值为$o_{t+1}$)公式为： $\sigma_{t+1}(i)=\max_{j\in1..n}{\sigma_t(j)a_{ji}b_{i(o_{t+1})}}$ 为了记住上一节点状态，定义$\theta_t(i)$: $\theta_t(i)=\arg\max_{j\in1..n}\sigma_{t-1}(j)a_{ji},i=1,2..n$

根据上面的定义，计算最优路径的算法为： (1)初始化， $\sigma_1(i)=\pi_{i1}b_{i}(o_1),i=1,2..n \\ \theta_1(i)=0$ (2)根据上面公式，递推，对于=2,3,..T， (3)终止， $P^*=\max_{i\in1,2..n}\sigma_T(i) \\ i_T^*=\arg\max_{i\in1,2..n}\theta_{T}(i)$ (4)最优路径回溯，从T-1到1， $i_t^*=\theta_{t+1}(i_t^*)$ 得到最优路径$I={i_1^*,i_2^*,..i_T^*}$。回溯的过程只需要从$T-1$开始，不需要任何计算，因为$\theta$中保存了到达当前最优路径状态的上一状态。

---

【参考】 1. HMM中Viterbi算法实现例子
2. 隐马尔可夫模型

---