公众号:尤而小屋
作者:Peter
编辑:Peter
大家好,我是Peter~
最近看了很多的关于因子分析的资料,整理出这篇理论+实战文章分享给大家。后续会出一篇PCA主成分分析的文章,将主成分分析和因子分析两种降维的方法进行对比。

因子分析
作为多元统计分析里的降维方法之一,因子分析可以应用于多个场景,如调研、数据建模等场景之中。
起源
因子分析的起源是这样的:1904年英国的一个心理学家发现学生的英语、法语和古典语成绩非常有相关性,他认为这三门课程背后有一个共同的因素驱动,最后将这个因素定义为“语言能力”。
基于这个想法,发现很多相关性很高的因素背后有共同的因子驱动,从而定义了**因子分析,这便是因子分析的由来。
基本思想
我们再通过一个更加实际的例子来理解因子分析的基本思想:
现在假设一个同学的数学、物理、化学、生物都考了满分,那么我们可以认为这个学生的理性思维比较强,在这里理性思维就是我们所说的一个因子。在这个因子的作用下,偏理科的成绩才会那么高。
到底什么是因子分析?就是假设现有全部自变量x的出现是因为某个潜在变量的作用,这个潜在的变量就是我们说的因子。在这个因子的作用下,x能够被观察到。
因子分析就是将存在某些相关性的变量提炼为较少的几个因子,用这几个因子去表示原本的变量,也可以根据因子对变量进行分类。
因子分子本质上也是降维的过程,和主成分分析(PCA)算法比较类似。
2种因子分析
因子分析又分为两种:
- 探索性因子分析:不确定在现有的自变量背后到底有几个因子在起作用,我们通过需要这种方法试图寻找到这几个因子
- 验证性因子分析:已经假设自变量背后有几个因子,试图通过这种方法去验证一下这种假设是否正确。
模型推导
假设有p个原始的变量xi(i=1,2,…p),它们之间可能独立也可能相关。将xi标准化后得到新的变量zi,我们可以建立如下的因子分析模型:
zi=ai1F1+ai2F2+⋯+aimFm+ciUi(i=1,2,⋯,p)
其中,我们可以定义以下几个术语:公共因子、特殊因子、载荷因子、载荷矩阵
1、第一点:Fj(j=1,2,…m)出现在每个变量的式子中且m<p,称之为公共因子
2、第二点:Ui(i=1,2,…p)仅仅与变量zi相关,称之为特殊因子
3、第三点:系数aij、ci(i=1,2…p,j=1,2,…m)称之为载荷因子
4、第四点:A=(aij)称之为载荷矩阵
上面的式子可以表示为:z=AF+CU
同时也就满足:
A=\left(a_{i j}\right)_{p \times m}, \quad C=\operatorname{diag}\left(c_{1}, c_{2}, \cdots, c_{p}\right)$$
我们通常需要对上述模型的进行假设:
1.各个特殊因子以及特殊因子和公共因子之间相互独立,即满足:
$$\left\{\begin{array}{l}\operatorname{Cov}(U)=\operatorname{diag}\left(\sigma_{1}^{2}, \sigma_{2}^{2}, \cdots, \sigma_{p}^{2}\right) \\ \operatorname{Cov}(F, U)=0\end{array}\right.$$
2、各公共因子都是均值为0、方差为1的独立正态随机变量,其协方差矩阵为单位矩阵$I_m$,即$F-N(0,I_m)$
3、m个公共因子对第i个变量方差的贡献称之为第i**贡献度**,记为$h_i^2$
$$h_{i}^{2}=a_{i 1}^{2}+a_{i 2}^{2}+\cdots+a_{i m}^{2}$$
4、特殊因子的方差称之为**特殊方差**或者**特殊值**($\sigma_{i}^{2},i=1,2,3…p$)
5、第i个变量的方差分解为:$\operatorname{Var} z_{i}=h_{i}^{2}+\sigma_{i}^{2}, i=1,2, \cdots, p$
具体的模型推导过程:https://blog.csdn.net/qq_29831163/article/details/88901245
### 因子载荷矩阵的重要性质
关于因子载荷矩阵的几个重要性质:
1、因子载荷$a_{ij}$是第i个变量与第j个公共因子的相关系数,反映的是第i个变量和第j个公共因子之间的重要性。**绝对值越大,表示相关性的密切程度越高**。
2、贡献度的统计意义
$$h_{i}^{2}=a_{i 1}^{2}+a_{i 2}^{2}+\cdots+a_{i m}^{2}=\sum_{i=1}^ma_{ij}^2$$
说明:变量$X_i$的贡献度就是因子载荷矩阵的第i行的元素的平方和
上式两边同时求方差:
$$\operatorname{Var}\left(X_{i}\right)=a_{i 1}^{2} \operatorname{Var}\left(F_{1}\right)+\cdots+a_{i m}^{2} \operatorname{Var}\left(F_{m}\right)+\operatorname{Var}\left(\varepsilon_{i}\right)$$
也就是:$1=\sum_{j=1}^{m} a_{i j}^{2}+\sigma_{i}^{2}$
可以看出来:公共因子和特殊因子对变量$X_i$的贡献度之和为1。如果$\sum_{i=1}^ma_{ij}^2$非常接近1,则$\sigma^2$非常小,则因子分析的效果非常好。
3、公共因子$F_{j}$方差贡献的统计意义
因子载荷矩阵中各列元素的平方和 $S_j=\sum_{i=1}^p a_{ij}^2$成为$F_(j)$对所有的$X_j$的方差贡献和,衡量$F_j$的相对重要性。
## 因子分析步骤
应用因子分析法的主要步骤如下:
- 对所给的数据样本进行**标准化处理**
- 计算样本的**相关矩阵R**
- 求相关矩阵R的**特征值、特征向量**
- 根据系统要求的**累积贡献度**确定主因子的个数
- 计算因子**载荷矩阵A**
- 最终确定因子模型
## factor_analyzer库
利用Python进行因子分析的核心库是:factor_analyzer
```python
pip install factor_analyzer
```
这个库主要有两个主要的模块需要学习:
- factor_analyzer.analyze(重点)
- factor_analyzer.factor_analyzer
官网学习地址:https://factor-analyzer.readthedocs.io/en/latest/factor_analyzer.html
## 案例实战
下面通过一个案例来讲解如何进行因子分析。
### 导入数据
本文中使用的数据是公开的数据集,下面是数据的介绍和下载地址:
- 数据集介绍: [https://vincentarelbundock.github.io/Rdatasets/doc/psych/bfi.](https://vincentarelbundock.github.io/Rdatasets/doc/psych/bfi.html)[html](https://vincentarelbundock.github.io/Rdatasets/doc/psych/bfi.html)
- 数据集下载: https://vincentarelbundock.github.io/Rdatasets/datasets.html
这个数据集收集了2800个人关于人格的25个问题。同时这些数据和隐藏的5个特征相关,
> Big Five Model is widely used nowadays, the five factors include: **neuroticism,extraversion,openness to experience,agreeableness and conscientiousness.**
特征之间的对应关系为:
- 认同性:agree=c(“-A1”,“A2”,“A3”,“A4”,“A5”)
- 勤奋的、有责任的:conscientious=c(“C1”,“C2”,“C3”,“-C4”,“-C5”)
- 外向的:extraversion=c(“-E1”,“-E2”,“E3”,“E4”,“E5”)
- 神经质、不稳定性:neuroticism=c(“N1”,“N2”,“N3”,“N4”,“N5”)
- 开放的:openness = c(“O1”,“-O2”,“O3”,“O4”,“-O5”)
事先我们并不知道这些隐形变量的对应关系,所以想要通过因子分析来找到25个变量后面的隐藏变量。下面开始进行因子分析的实战过程:
## 导入库
导入数据处理和分析所需要的库:
```python
# 数据处理
import pandas as pd
import numpy as np
# 绘图
import seaborn as sns
import matplotlib.pyplot as plt
# 因子分析
from factor_analyzer import FactorAnalyzer
```
## 数据探索
### 数据信息
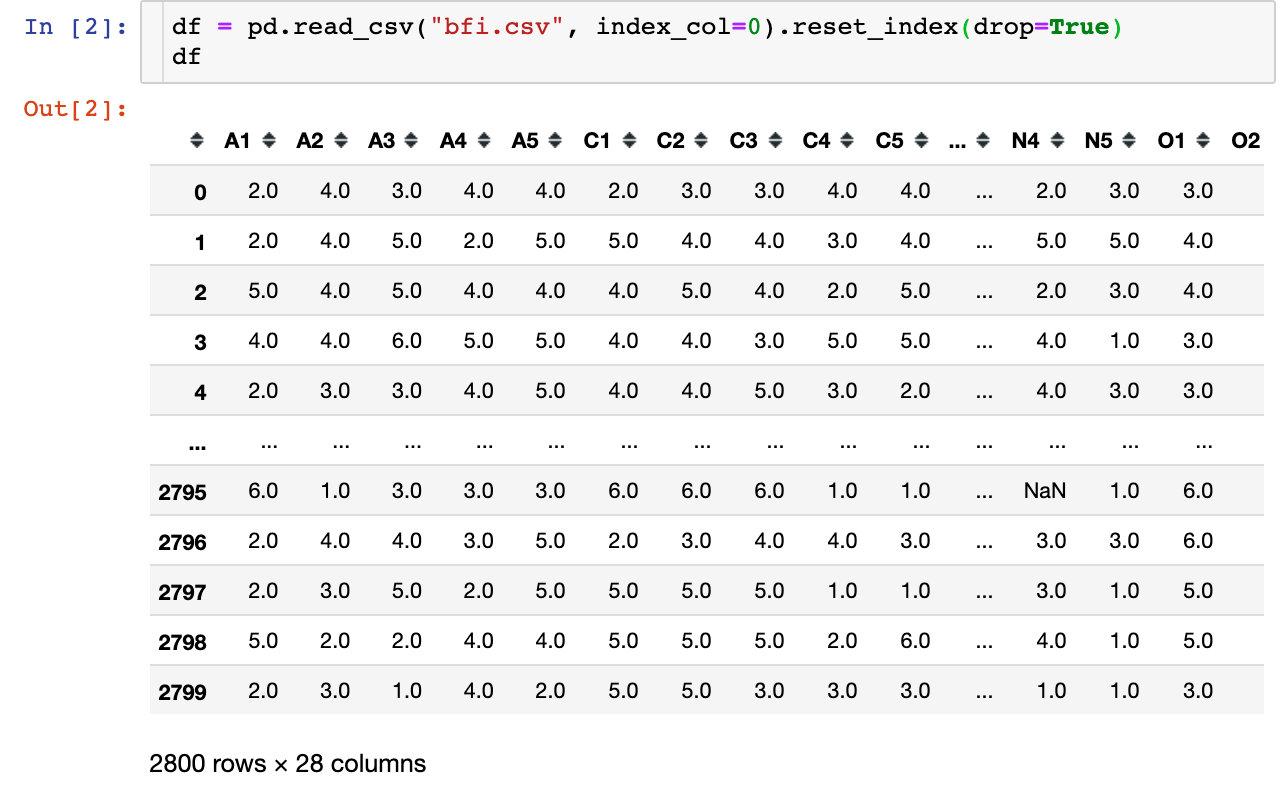
首先我们先导进数据:总共是2800条数据,28个特征属性
```python
df = pd.read_csv("bfi.csv", index_col=0).reset_index(drop=True)
df
```
查看下数据的缺失值情况:**大部分的字段都是存在缺失值的**
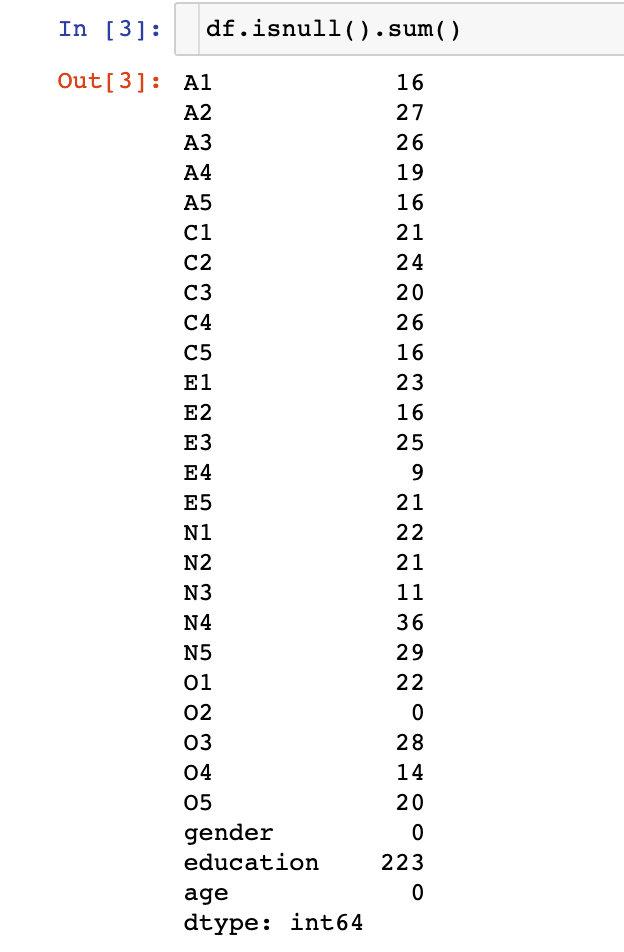
### 数据预处理
数据预处理包含去除3个无效的字段(对分析没有任何作用:age、gender、education),同时去掉存在空值的数据:
```python
# 去掉无效字段
df.drop(["gender","education","age"],axis=1,inplace=True)
# 去掉空值
df.dropna(inplace=True)
```
## 充分性检测
在进行因子分析之前,需要先进行充分性检测,主要是检验相关特征阵中各个变量间的相关性,是否为单位矩阵,也就是检验各个变量是否各自独立。通常是两种方法:
- Bartlett's球状检验(巴特利球形检验)
- KMO检验
### Bartlett's球状检验
检验总体变量的相关矩阵是否是单位阵(相关系数矩阵对角线的所有元素均为1,所有非对角线上的元素均为零);即检验各个变量是否各自独立。
如果不是单位矩阵,说明原变量之间存在相关性,可以进行因子分子;反之,原变量之间不存在相关性,数据不适合进行主成分分析
```python
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value, p_value = calculate_bartlett_sphericity(df)
chi_square_value, p_value
# 结果
(18170.96635086924, 0.0)
```
我们发现统计量p-value的值为0,表明变量的相关矩阵不是单位矩阵,即各个变量之间是存在一定的相关性,我们就可以进行因子分析。
### KMO检验
检查变量间的相关性和偏相关性,取值在0-1之间;KOM统计量越接近1,变量间的相关性越强,偏相关性越弱,因子分析的效果越好。
> **Kaiser-Meyer-Olkin (KMO) Test** measures the suitability of data for factor analysis. It determines the adequacy for each observed variable and for the complete model.
>
> KMO estimates the proportion of variance among all the observed variable. Lower proportion id more suitable for factor analysis. KMO values range between 0 and 1. Value of KMO less than 0.6 is considered inadequate.
通常取值从0.6开始进行因子分析
```python
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model=calculate_kmo(df)
kmo_all
```
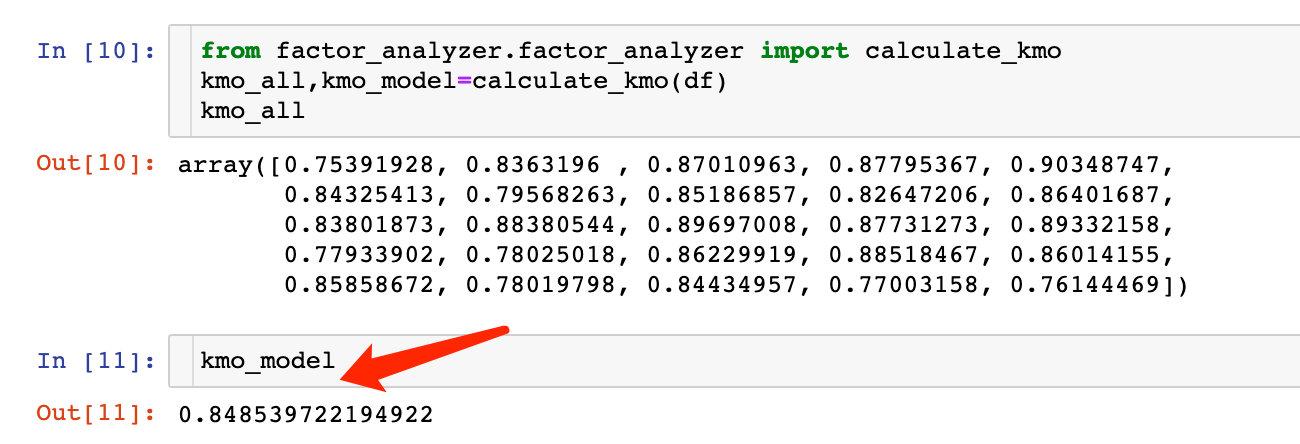
KMO大于0.6,也说明变量之间存在相关性,可以进行分析。
## 选择因子个数
在数据说明中,我们已经知道了这些变量是和5个隐藏的因子相关。但是很多情况下,我们并不知道这个个数,需要自己进行探索。
方法:**计算相关矩阵的特征值,进行降序排列**
### 特征值和特征向量
```python
faa = FactorAnalyzer(25,rotation=None)
faa.fit(df)
# 得到特征值ev、特征向量v
ev,v=faa.get_eigenvalues()
```

### 可视化展示
我们将特征值和因子个数的变化绘制成图形:
```python
# 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), ev)
plt.plot(range(1, df.shape[1] + 1), ev)
# 显示图的标题和xy轴的名字
# 最好使用英文,中文可能乱码
plt.title("Scree Plot")
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")
plt.grid() # 显示网格
plt.show() # 显示图形
```
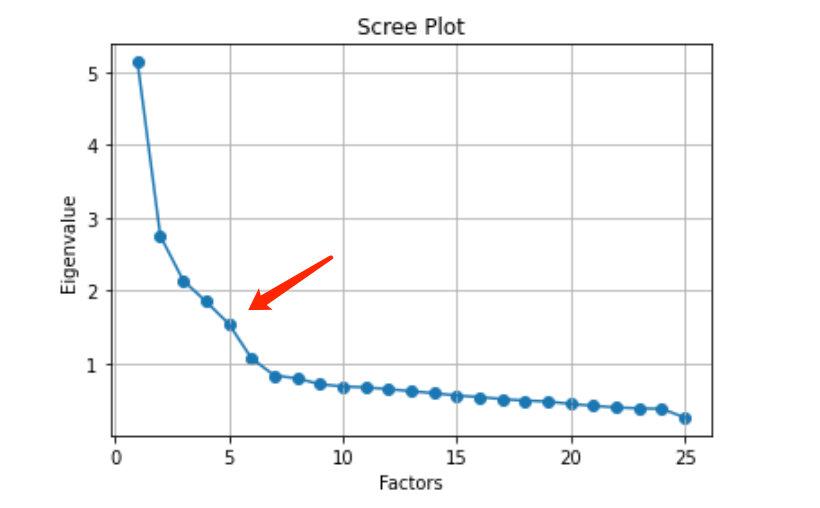
从上面的图形中,我们明确地看到:选择5个因子是最合适的
## 建模
### 因子分析-fit
我们选择5个因子来进行因子分子的建模过程,同时指定矩阵旋转方式为:**方差最大化**

ratation参数的其他取值情况:
- varimax (orthogonal rotation)
- promax (oblique rotation)
- oblimin (oblique rotation)
- oblimax (orthogonal rotation)
- quartimin (oblique rotation)
- quartimax (orthogonal rotation)
- equamax (orthogonal rotation)
### 查看因子方差-get_communalities()
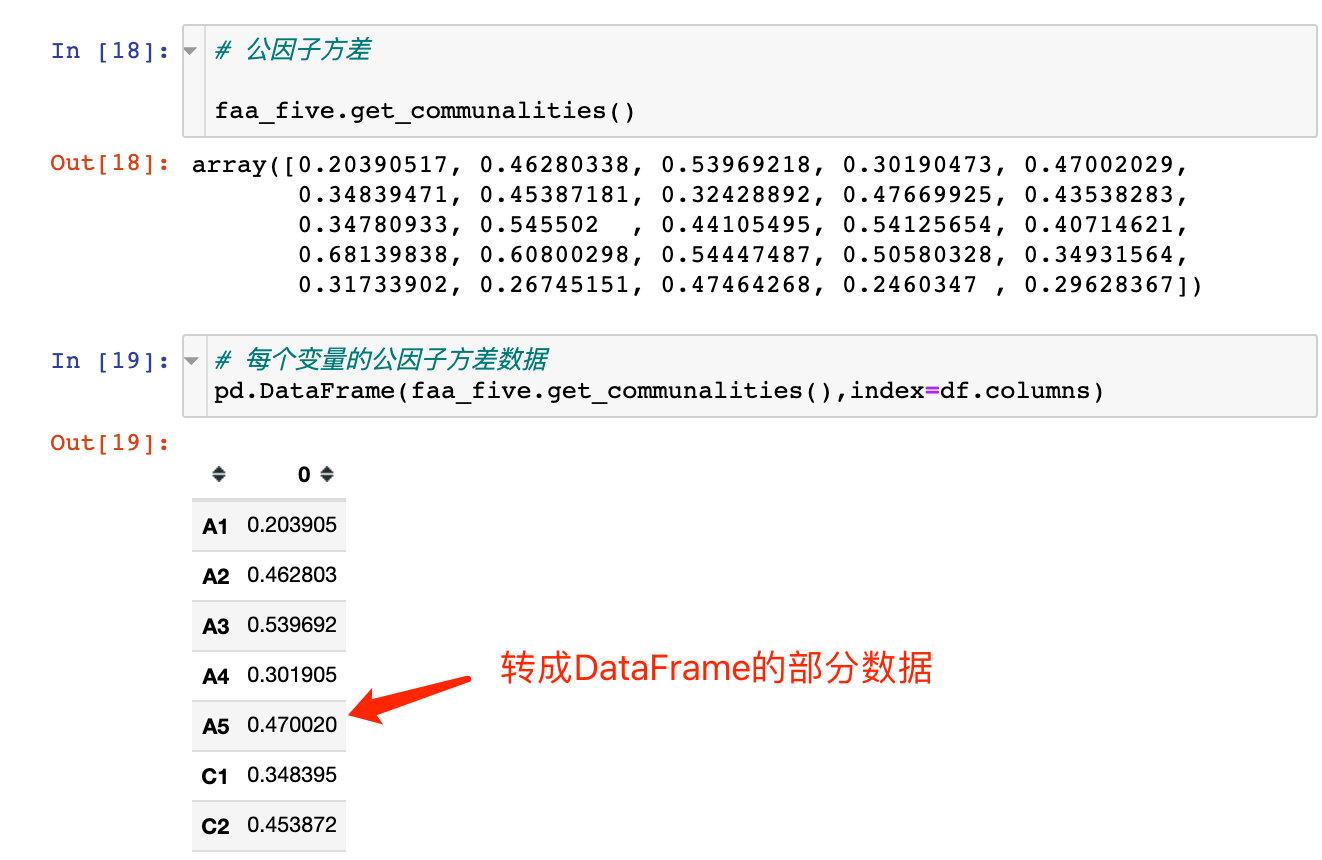
上面执行fit建模后,我们查看每个因子的方差,使用方法:get_communalities()
### 查看特征值-get_eigenvalues
查看变量的特征值:

### 查看成分矩阵-loadings
现在有25个变量,5个隐藏变量(因子),查看它们构成的成分矩阵:
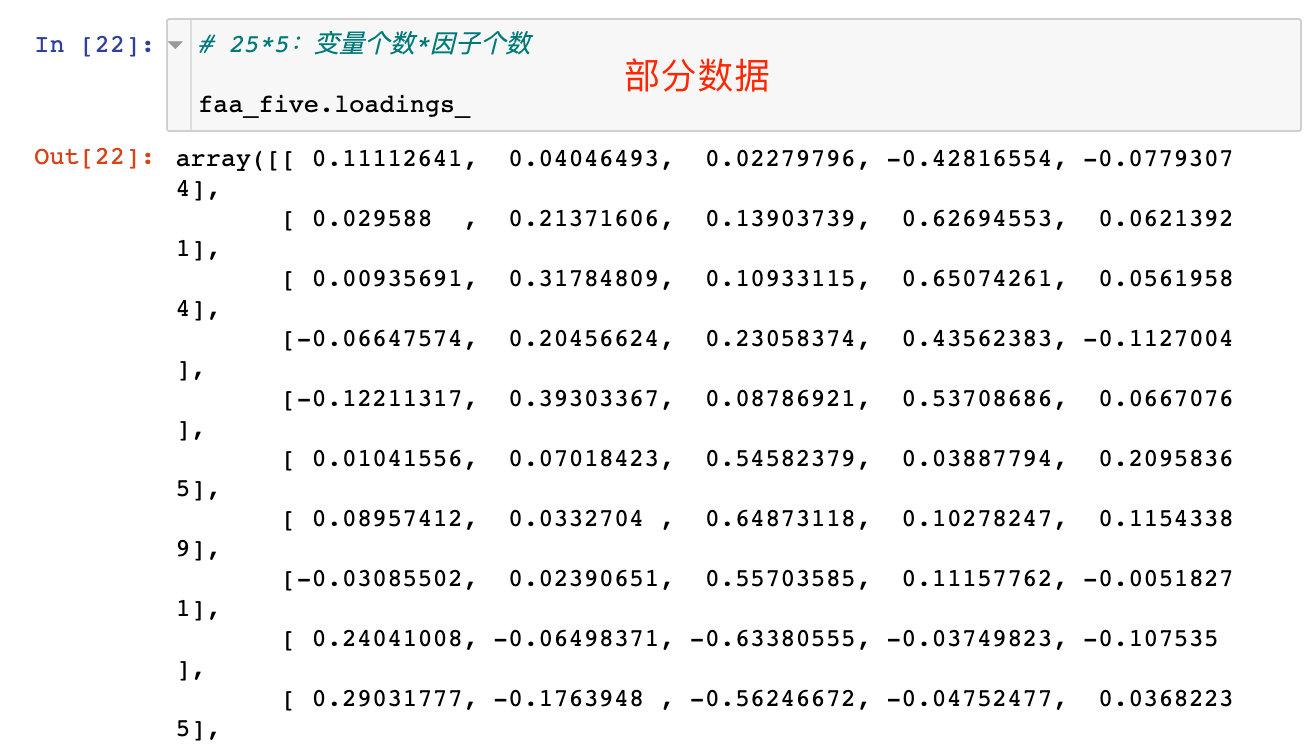
如果转成DataFrame格式,index就是我们的25个变量,columns就是指定的5个因子factor。转成DataFrame格式后的数据:

### 查看因子贡献率-get_factor_variance()
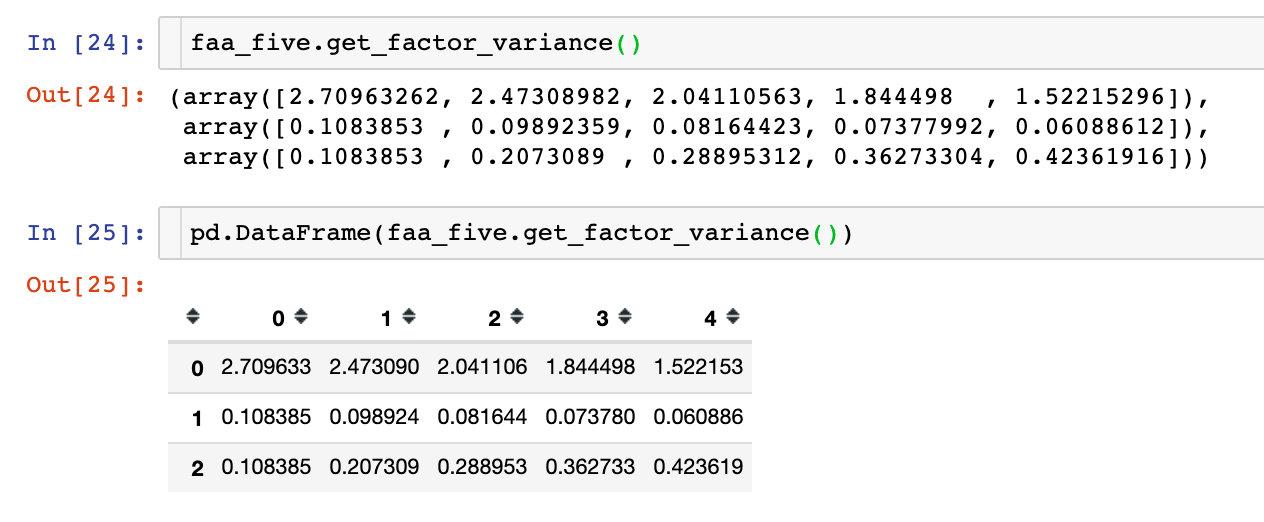
通过理论部分的解释,我们发现每个因子都对变量有一定的贡献,存在某个贡献度的值,在这里查看3个和贡献度相关的指标:
- 总方差贡献:variance (numpy array) – The factor variances
- 方差贡献率:proportional_variance (numpy array) – The proportional factor variances
- 累积方差贡献率:cumulative_variances (numpy array) – The cumulative factor variances

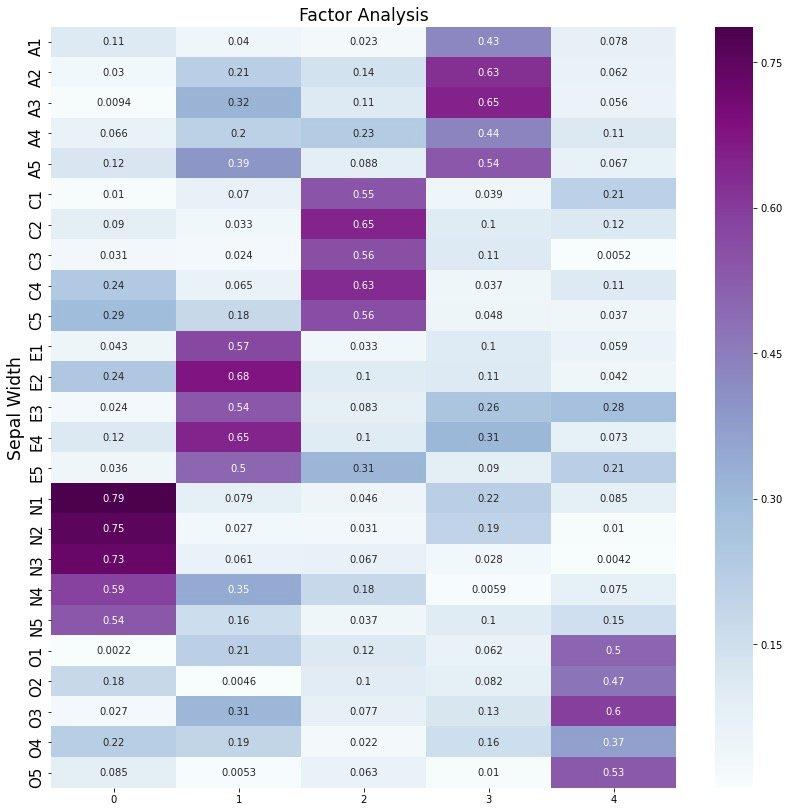
## 隐藏变量可视化
为了更直观地观察每个隐藏变量和哪些特征的关系比较大,进行可视化展示,为了方便取上面相关系数的绝对值:
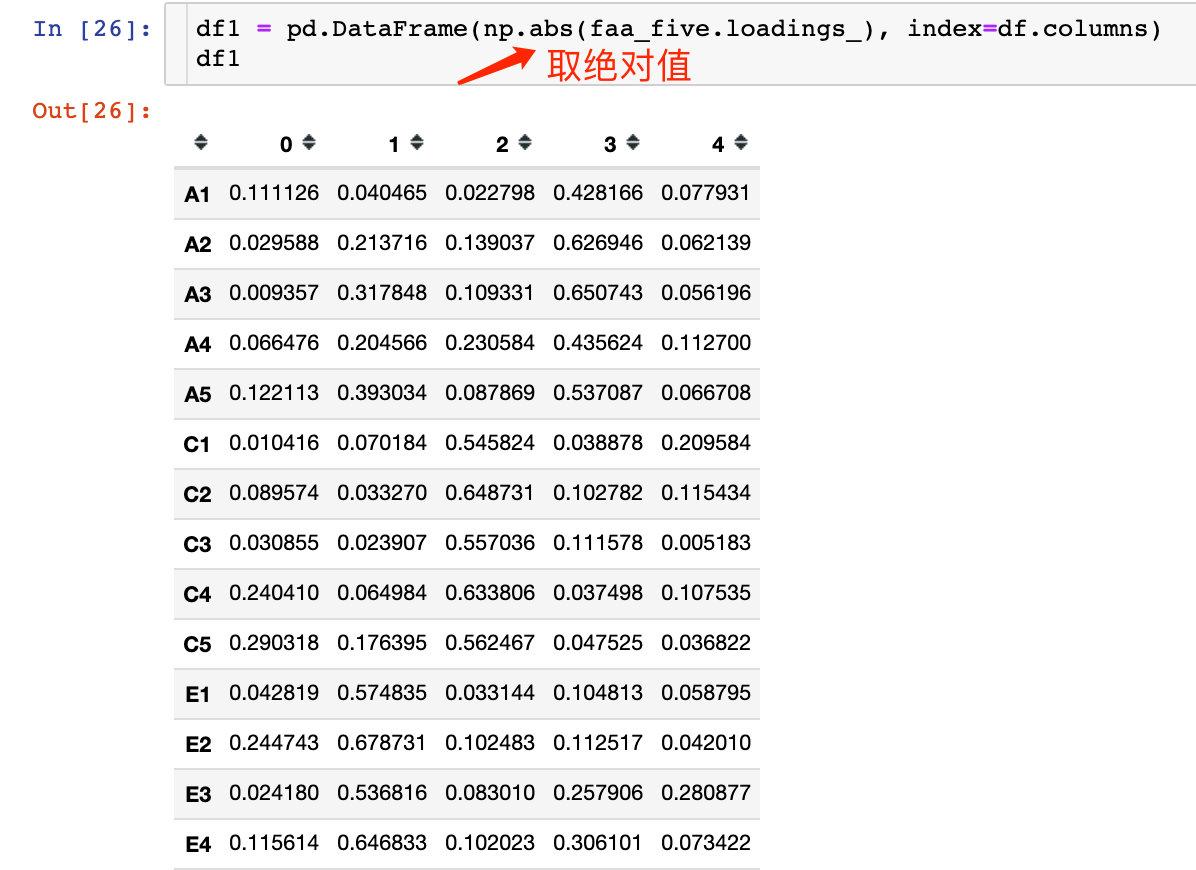
然后我们通过热力图将系数矩阵绘制出来:
```python
# 绘图
plt.figure(figsize = (14,14))
ax = sns.heatmap(df1, annot=True, cmap="BuPu")
# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")
# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()
# 保存图片
# plt.savefig("factorAnalysis", dpi=500)
```
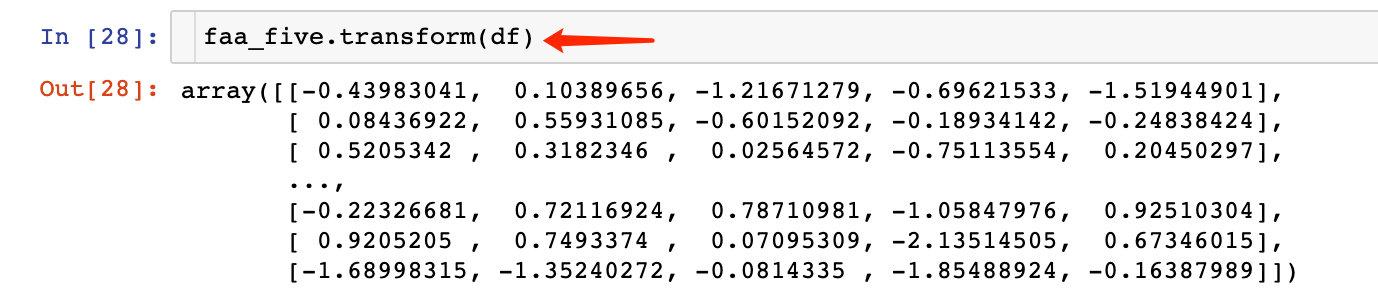
## 转成新变量-transformn
上面我们已经知道了5个因子比较合适,可以将原始数据转成5个新的特征,具体转换方式为:
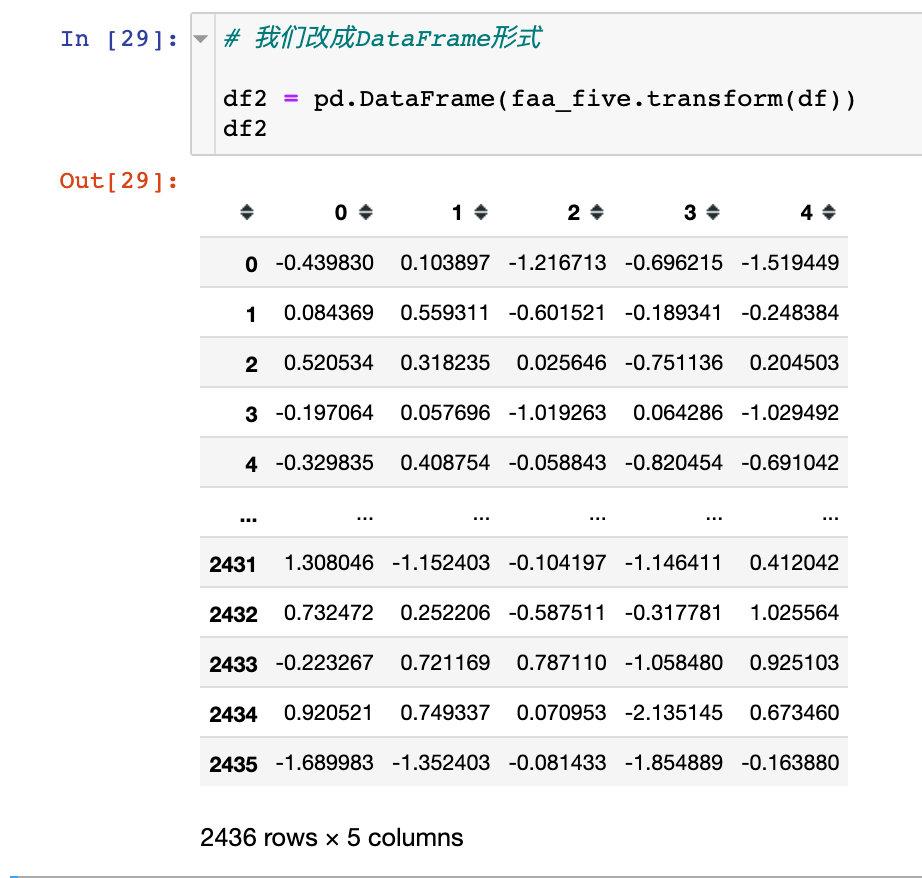
转成DataFrame格式后数据展示效果更好:仍然是2436条数据,5个特征(新特征)
至此,我们完成了如下的工作:
1. 原数据的相关性检测
2. 因子个数的探索
3. 因子分析的建模过程
4. 隐藏变量的可视化
5. 转成基于5个新变量的数据
## 参考资料
1、Factor Analysis:https://www.datasklr.com/principal-component-analysis-and-factor-analysis/factor-analysis
2、多因子分析:https://mathpretty.com/10994.html
3、`factor_analyzer package`的官网使用手册:https://factor-analyzer.readthedocs.io/en/latest/factor_analyzer.html
4、浅谈主成分分析和因子分析:https://zhuanlan.zhihu.com/p/37755749