以下内容主要来自:
Time Series Analysis (TSA) in Python - Linear Models to GARCH
目录
Autoregressive Conditionally Heteroskedastic Models - ARCH(p)
Generalized Autoregressive Conditionally Heteroskedastic Models - GARCH(p, q)
Autoregressive Conditionally Heteroskedastic Models - ARCH(p)
ARCH(p) (自回归条件异方差) 模型可以简单看作是应用于时间序列方差的 AR(p) 模型。另一种思路是当前 t 时刻时间序列的方差是基于过去一段时间的方差。ARCH(1) 的公式是:
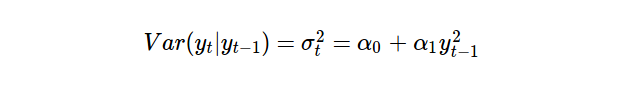
假设序列的均值为 0 ,那么我们可以这个模型表示为:
# Simulate ARCH(1) series
# Var(yt) = a_0 + a_1*y{t-1}**2
# if a_1 is between 0 and 1 then yt is white noise
np.random.seed(13)
a0 = 2
a1 = .5
y = w = np.random.normal(size=1000)
Y = np.empty_like(y)
for t in range(len(y)):
Y[t] = w[t] * np.sqrt((a0 + a1*y[t-1]**2))
# simulated ARCH(1) series, looks like white noise
tsplot(Y, lags=30)
ARCH(1) 的图像如下:
ARCH(1)平方的图像如下:
注意 ACF和 PACF 在滞后1处展现了显著性,说明方差的AR(1)的模型可能是合适的。
Generalized Autoregressive Conditionally Heteroskedastic Models - GARCH(p, q)
简单来说,GARCH(p, q) 是一个应用于时间序列方差的ARMA模型。它具有一个自回归项和一个移动平均项。AR(p)表示残差的方差(平方误差)或者仅仅是时间序列的平方。MA(q)表示这个过程的方差。最基本的GARCH(1, 1)表示为:
其中,w 指的是白噪声,a 和 b 分别是GARCH模型的参数。另外,a1 + b1必须小于1,否则的话这个模型就是不稳定的。我们模拟一个GARCH(1, 1)的过程:
# Simulating a GARCH(1, 1) process
np.random.seed(2)
a0 = 0.2
a1 = 0.5
b1 = 0.3
n = 10000
w = np.random.normal(size=n)
eps = np.zeros_like(w)
sigsq = np.zeros_like(w)
for i in range(1, n):
sigsq[i] = a0 + a1*(eps[i-1]**2) + b1*sigsq[i-1]
eps[i] = w[i] * np.sqrt(sigsq[i])
_ = tsplot(eps, lags=30)
GARCH(1, 1)的图像如下:
可以看出真个过程近似白噪声。下面看一下平方后的图像:
可以看出明显的自相关性,在ACF和PACF中的显著性表明我们需要用AR和MA两种成分来作为我们的模型。 让我们看看能否用一个 GARCH(1,1) 模型来回复这个过程的参数。
下面我们利用了 ARCH package中的 arch_model 函数。
# Fit a GARCH(1, 1) model to our simulated EPS series
# We use the arch_model function from the ARCH package
am = arch_model(eps)
res = am.fit(update_freq=5)
p(res.summary())
下面,让我们用一个 SPY收益作为例子。这个过程遵循:
迭代选择最适合的ARIMA模型的p,d,q组合。
根据最低AIC的ARIMA模型阶数来设置GARCH模型的阶数。
用GARCH(p,q)来拟合我们的时间序列。
检验模型的残差和平方残差的自相关性。
注意,我们选择了一段特定的时间序列来更好地强调重点。然而,这个结果会由于我们选择的时间阶段而不同。
def _get_best_model(TS):
best_aic = np.inf
best_order = None
best_mdl = None
pq_rng = range(5) # [0,1,2,3,4]
d_rng = range(2) # [0,1]
for i in pq_rng:
for d in d_rng:
for j in pq_rng:
try:
tmp_mdl = smt.ARIMA(TS, order=(i,d,j)).fit(
method='mle', trend='nc'
)
tmp_aic = tmp_mdl.aic
if tmp_aic < best_aic:
best_aic = tmp_aic
best_order = (i, d, j)
best_mdl = tmp_mdl
except: continue
p('aic: {:6.5f} | order: {}'.format(best_aic, best_order))
return best_aic, best_order, best_mdl
# Notice I've selected a specific time period to run this analysis
TS = lrets.SPY.ix['2012':'2015']
res_tup = _get_best_model(TS)
# aic: -5255.56673 | order: (3, 0, 2)
拟合的ARIMA(3,0,2)图像如下:
看起来像白噪音过程:
拟合的ARIMA(3,0,2)的平方的图像如下:
平方后的残差展现出了自相关性,下面拟合一个 GARCH 模型看一下效果。
# Now we can fit the arch model using the best fit arima model parameters
p_ = order[0]
o_ = order[1]
q_ = order[2]
# Using student T distribution usually provides better fit
am = arch_model(TS, p=p_, o=o_, q=q_, dist='StudentsT')
res = am.fit(update_freq=5, disp='off')
p(res.summary())
在处理值很小的数字时会出现收敛警告,乘以一个10作为因子可以放大这个度量,有时会很有帮助。然而我们这个例子中不需要这么做,下面是模型的残差:
GARCH(3,2)拟合 spy 收益
上面看起来像是白噪音,下面我们看一下平方后的残差的 ACF 和 PACF:
看来我们找到了一个合适的模型来拟合我们的数据,平方后的残差并没有显示出明显的自相关性。
References
- Quantstart.com - www.quantstart.com/articles#ti…
- Harvard Lectures in Python - iacs-courses.seas.harvard.edu/courses/am2…
- Penn State Stats - onlinecourses.science.psu.edu/stat510/nod…
- stationary pic + tsplot - www.seanabu.com/2016/03/22/…
- stationary quote, etc - people.duke.edu/~rnau/411di…
- interpreting qq plots - stats.stackexchange.com/questions/1…
- Kaplan SchweserNotes (Level 2) - Quantitative Methods