用SciPy的概率分布进行情景分析

蒙特卡洛,图片由Luka Nguyen来自Pixabay,可免费用于商业用途
本教程将演示我们如何在Python中建立蒙特卡洛模拟模型。我们将
- 使用SciPy的内置分布,特别是。正态分布、Beta分布和Weibull分布。
- 为β-PERT分布添加一个新的分布子类。
- 通过拉丁高立方抽样法抽取随机数。
- 并建立三个蒙特卡洛模拟模型。
0.依赖性
该脚本除了导入SciPy的_统计_库外,还导入了我们的全天候软件包pandas和numpy。
蒙特卡洛模拟的概念

图片来自Pixabay的Hans Braxmeier,可免费用于商业用途
蒙特卡洛(MC)方法是一种模拟技术,它为一个模型的_输出_变量构建概率分布,其中一些_输入_参数是随机变量。MC方法有时被称为_多概率模拟_技术,因为它整合了多个随机变量,这些随机变量的综合效应不容易被一个闭合式方程所描述。
MC方法是由约翰-冯-诺伊曼和斯坦尼斯-乌兰在20世纪40年代末发明的,当时他们正在洛斯阿拉莫斯实验室工作。当他们试图用确定性的方法来计算中子碰撞时,他们遇到了一个死胡同。乌瓦姆的想法是使用随机抽样,由早期的 "超级计算机 "ENIAC支持,以获得近似的解决方案。政府的保密规定要求使用一个代号;冯-诺依曼和乌兰的一位同事建议使用_蒙特卡洛_这个名字,乌兰的叔叔在第二次世界大战前经常去那里的赌场:他 "只需要去蒙特卡洛 "赌博。(Ułam)
一个MC模拟问题的例子:一家企业想模拟一种新产品未来的成功,于是建立了如下的模拟模型。
- 预期的销售量,v,是一个随机变量,遵循β-PERT分布,由3点估计得出。
- 产品的价格p将受到谈判的影响--一些客户会要求数量折扣或提前付款折扣;计划人员决定将公司将实现的平均价格的不确定性建模为一个平均值为20、标准差为2的正态随机变量。
- 产品的原材料成本,m,将受到即将到来的供应商价格上涨的影响,由另一个正态分布来估计。
- 该模型应提供多种结果:收入、利润、总成本。
一般来说,模拟模型接受定义为随机变量的输入参数;然后它为每个输出变量返回一个概率分布,每个输出变量都是其输入参数的函数。该函数可以是一个简单的和或乘积,也可以是输入的指数化,或者--正如我们将在一个例子中看到的--一个包括嵌套随机变量的高阶函数。目标变量将表现出一个密度函数,描述输入变量的分布如何相互影响。
仿真模型通过对输入分布的抽样得出输出分布。1,000或100,000次迭代提供了描述每个输入变量行为的数据点。输出变量的方程式将这些输入转化为输出变量的尽可能多的样本。一旦我们得到这个样本,我们就可以像任何内置的SciPy分布一样审查它的模式--它的平均值、量值和离群值的倾向。
2.拉丁高立方采样
NumPy的_随机_库提供了用均匀随机数填充数组的方法。SciPy的分布对象都带有生成随机变量的_rvs()_方法。然而,蒙特卡洛模拟需要大量的随机数数组,对于这些数组,_分层抽样_方法,如**拉丁超立方抽样(LHS)**是最好的方法。
LHS将样本空间划分为不重叠的单元,每个单元的概率相等。LHS确保了随机数更均匀地从样本空间的完整范围内抽取。它可以防止采样的随机数_结块_ ,而结块会扭曲频率曲线。LHS采样将导致更准确的模拟结果。它将导致更低的标准误差,并减少迭代次数。
为了演示,我们通过使用SciPy的LatinHyperCube采样器创建一个10个随机数的小数组。

均匀(0;1)的随机数在生成之后,可以重新缩放以填充更宽的范围,例如0到100之间。不过对于我们的目的来说,0到1之间的标准随机数可以满足要求。

在下一章,我们将使用LHS样本来生成特定分布的随机变量:PERT、正态和Weibull函数。
3.对模拟中的不确定性进行建模的概率分布
3.1 用于模拟专家估计的PERT分布
我以前的文章--"用β-PERT分布为专家估计值建模"--是一个解释PERT分布 的教程(Python情景分析。用β-PERT分布对专家估计值进行建模|走向数据科学)。)
如果一个领域、过程或行业专家能够为一个随机过程提供一个所谓的_三点_估计(Three -point estimation),包括最坏情况、可能情况和最佳情况的结果,那么PERT函数就可以把这些点连接起来,相当地。它将把这些点转化为我们可以分配给仿真模型中随机变量的概率分布。
SciPy的123个分布的目录并不包括PERT函数。因此,我们把它创建为一个新的子类,继承自SciPy的_rv_continuous_父类。
对于我们的例子,我们用四个参数实例化PERT子类,预测一个新产品的销售量。
我们选择这个PERT分布来模拟预期的销售量,最可能的值是12,000个,框在最小8,000个和最大18,000个之间。

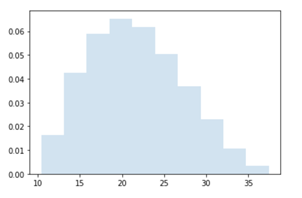
它的期望值,即平均值,将是12,333个销售单位。它有一个小的正偏度,仍然类似于正态分布;和一个适度的负的超额峰度-0.62,这使得它成为一个板状或笨重的分布,在其尾部容易出现比正态分布更少的离群值。
第3行抽取了一个N=10,000个均匀随机变量的LHS样本。然后第4行将数组作为其输入参数。百分点 _函数ppf()_将10,000个标准均匀数解释为概率,并计算出10,000个PERT量值,并将其填充到数组randP中。
直方图显示了模拟的 PERT 分布的形状。
3.2 正态分布
我们应用同样的方法(除去需要创建一个新的分布子类),从正态分布中抽取10,000个LHS样本,我们希望它能反映出销售价格和原材料单位成本中固有的不确定性。平均售价将为20欧元,标准差为2欧元。


第二个正态分布模拟原材料单位成本,平均值为13欧元,标准差为1.40欧元。
3.3 模拟 1--对随机变量的和与积进行建模
我们创建了三个随机变量,代表三个因素的不确定性,这些因素将决定新产品产生利润的几率或损失的风险。
- 1x PERT--用于销量v。
- 2个正态变量--代表销售价格p和原材料单位成本m。
我们假设其他成本,即那些与供应商价格无关的成本,可以通过一个确定性的变量o来反映。
为了计算模拟模型的目标变量--产品的毛利GP--,我们将这些随机变量联系在一起,如下所示。
- v = 数量,p = 价格,m = 原材料单位成本,o = 其他单位成本
- GP = v * (p - m - o)
作为一个次要的输出变量,我们可以在模拟收入R的同时模拟GP。一般来说,一旦我们定义了它们的输入随机变量,我们就可以用任意多的输出变量来设置仿真模型。每个输出变量可以由一个或多个输入随机变量组合而成,并将由其自身的10000个变量阵列来描述。
- R = v * p
这就建立了我们的简单模拟模型。

为了审查返回毛利随机变量GP分布的数组的属性,我们编写了一个函数_dist_properties()_ ,它将读取数组并返回其矩和选定的量值。
对于偏度和峰度,我们利用SciPy的_skew()和kurtosis()_ 函数,我们需要借助numpy的 _asscalar()_转换方法将其结果从数组变成平面数字。我们在字典_dict_moments_中收集它们的值,并在其中加入度量的名称。第14行的列表理解将字典的内容逐行打印出来。
然后我们在第17行以下计算量值,把它们收集到另一个字典 _dict_quantiles_中,并通过第27行的列表理解来打印它。
我们将这两个字典,即矩值和量值合并,形成一个综合字典,即_dict_metrics_。
medium.com/media/147cd…medium.com/media/712a4…


平均利润将达到49,250欧元,接近于中位数。
偏度和峰度都相当适中,意味着与正常分布相比,离群值的倾向不大。
表中的量值显示,如果销售价格和原材料单位成本同时趋于最坏的结果,新产品将产生5%的风险。利润将超过10,731欧元,概率为90%(10%的量纲)。
在下一章,我们将更进一步,建立一个高阶模拟模型。虽然第一个模型从单纯的随机变量的和与乘积中组装了输出变量,但我们现在将开发一个包括_嵌套_随机变量的模拟模型。
3.5 仿真2--嵌套分布
如果你读过我以前的文章(Intro to Probability Distributions and Distribution Fitting with Python's SciPy ),你会记得我们曾应用Weibull分布来解决失效时间或部件寿命 问题。一个部件的寿命通常可以用Weibull分布来建模,其形状反映了_故障率_,而比例参数则设定了所谓的_特征寿命_。
第一艘飞往火星的太空船将配备电子电路板,其特征寿命可能为50,000个工作小时。为了估计飞船设计中需要的冗余度,我们将模拟所有电路中的哪一部分将在多少小时后烧毁。
让我们假设,与现实相当的是,Weibull分布的两个参数--形状和特征寿命--并不确定。因此,我们将把这些分布参数作为自己的随机变量来估计。Weibull形状和它的规模可以在其分布模式设定的边界内波动。
- 对于形状参数,工程团队估计它应该是关于平均值为1.5,标准差为0.1的正态分布。
- 对于特征寿命,我们采用工程团队提供的3点估计,即在45,000、50,000和60,000小时运行时的最大、可能和最小值。然后我们推导出一个PERT分布来反映不确定性的范围。
两个辅助函数通过拉丁超立方体抽样,分别抽取10,000个随机变量。
- _wei_shp()_返回正态分布的形状参数。
- _wei_charlife()_返回特征寿命的PERT变量阵列。
- 我们将Weibull位置参数(又称等待时间)设置为0,意味着产品故障在生产完成和质量测试开始后会立即浮现。

在第7行中,我们将随机变量集合在一个Weibull输出变量中,用于计算故障前的时间。Weibull函数为获得其形状和比例参数,调用了辅助函数。目标变量_rand_CL_将保存一个由10,000个模拟输出组成的数组,代表组件的寿命,单位为小时。
有三个嵌套分布的结果:一个PERT和和一个正态随机变量作为Weibull分布的参数。我们可以把这个结果称为灵活或随机的Weibull分布,而不是参数为点值的固定分布。
对于如何审查结果的属性,我们可以选择两种方案。
- 将其作为一个数组进行分析,就像我们对之前的模拟结果一样
- 应用SciPy的_rv_histogram类_,_该类_将输出数组分为直方图,并将其变成一个 "真正的 "SciPy概率分布,为此我们可以调用pdf和ppf等分布函数。
让我们来看看柱状图类。

该图以蓝色显示了我们在数组rand_CL中模拟的分档寿命。橙色显示的是_rv_histogram_类从数组中导出的概率密度函数。
一个函数_histdist_properties()_ 计算了 histdist_概率分布的属性。这个函数在某些方面与我们之前编写的函数_distribution_properties() 不同。_rv_histogram_类并不是在所有情况下都提供相同的分布属性。例如,最小值和最大值必须从._support()_方法中检索出来。
我们调用_histdist_properties()函数,获得表格中的度量。数据框架不仅包含累积分布函数和量值,而且还有一列随机变量。抽样函数.rvs()_使我们能够从我们的输出分布中抽取一些随机数--如果需要的话,也可以是几千个,不过没有LHS方法的分层抽样。

上面,我们分析了_rv_histogram_从数组中得出的连续 分布。如图所示,分布曲线与数组数据并不完全相同。
下面,我们在10,000个输出数字的原始数组上调用函数_dist_properties()_,并解释矩和量值。

- 组件的平均寿命将达到45,647小时。
- 寿命将是右偏的,自然,有超过100,000小时的离群值。
- 峰度是独特的--分布是倾斜的,在其尾部有一个长期生存的组件的倾向。
- 11,076小时后,10%的组件将被烧毁。
任务控制中心通知我们,11000小时的运行将标志着关键的门槛。在完成这些利用小时后,电路将不再是关键任务。这些数量意味着,就电路板而言,太空船的设计应考虑到至少10%的冗余度:通过增加备用电路板,这些电路板将自动开启,作为那些开始失效的电路板的替代品。
所以我们的太空船几乎已经准备好发射了。

图片由Peter H从Pixabay拍摄,可免费用于商业用途
3.6 模型3:固定参数模拟
作为最后一项练习,让我们检查一下Weibull模型对其形状和特征寿命的不确定性有多敏感。
我们将用一个 "固定形式 "的Weibull分布进行蒙特卡洛模拟。
- 形状参数将被固定为平均值1.5。
- 特征寿命:为 PERT 分布的平均值。50,500小时。
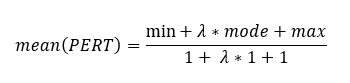

我们再次调用_dist_properties()_函数,并将其指标插入一个数据框中,这样我们就可以将固定的Weibull和之前嵌套的、因此是 "灵活的 "Weibull进行并列比较。

正如预期的那样,我们看到固定Weibull变量的标准差较低,它是在形状和尺度参数没有不确定性的情况下生成的。但差异很小。显然,灵活Weibull模型的形状和尺度参数的不确定性相当紧密地凝聚在我们在固定Weibull模型中使用的平均值周围。较低的偏度和峰度表明离群和不对称的倾向有所减少。
用不同的参数值或不同的分布进行模拟,可能会显示出由增加的不确定性引起的更大差异。
4.4.结论
今天的教程到此结束。
我们经历了三个蒙特卡洛模拟的例子,是用SciPy库提供的工具箱创建的。
- 第一个模型--利润模拟--展示了随机变量的简单和与积。
- 第二个模拟--Weibull失败前的时间--解释了嵌套随机变量的概念,当概率分布的参数本身就是随机变量时。
- 第三次模拟做了一个大胆的假设:分布的参数是精确已知的。如果我们在模拟模型中忽略了不确定性的来源,我们就有可能低估可能结果的分布,不过,除非不确定性浓缩为参数的平均值。
Jupyter笔记本可从GitHub下载:h3ik0th/MonteCarloSim。用SciPy进行蒙特卡洛模拟 (github.com)
- 蒙特卡洛,图片由Luka Nguyen来自Pixabay,可免费用于商业用途
- 蒙特卡洛赌场, 图片来源:Hans BraxmeierfromPixabay, 可免费用于商业用途
- 工厂, 图片来源:Peter HfromPixabay, 可免费用于商业用途
- 所有其他图片:由作者提供
由Python驱动的蒙特卡洛模拟最初发表在Medium上的Towards Data Science,在那里人们通过强调和回应这个故事来继续对话。