小知识,大挑战!本文正在参与“程序员必备小知识”创作活动
本篇文章中,我们将介绍监督学习模型中广泛使用的正则化技术以及这些技术之间的关键区别。
当你的数据集的特征维度数量较大时,为了能够创建一个低复杂度的(尽量简约的)模型,可以使用一些用于解决过拟合问题与实现特征选择的正则化技术:
- L1 正则(L1 Regularization)
- L2 正则(L2 Regularization)
对于回归模型,若其采用L1 正则,则被称为Lasso 回归,若其采用L2 正则,则被称为Ridge回归(岭回归) 。
两者的关键区别在于惩罚项(penalty term) 的不同。
岭回归使用回归系数的“幅度平方(squared magnitude)”作为损失函数的惩罚项。下图的高光部分表示的即为L2 正则:

此处,如果lambda为零,那么上述公式其实就可以被看作是一个普通的OLS(ordinary least squares 普通最小二乘法)。反之,如果lambda非常大,那么它就会使得惩罚项的权重过高,导致模型欠拟合。说了这么多,无非是为了阐明如何选择大小合适的lambda是个很重要的问题。毕竟,选择合适的惩罚项,能够很好的避免过拟合的问题。
Lasso 回归(Least Absolute Shrinkage and Selection Operator 最小绝对值收缩和选择算子)使用回归系数的“幅度的绝对值(absolute value of magnitude)”作为损失函数的惩罚项。
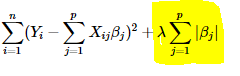
同样的,lambda为零时,上式就是一个普通的OLS,lambda非常大时又会导致欠拟合。
L1 正则与L2 正则的关键区别在于,使用L1 正则的Lasso回归会将不太重要的特征的系数直接缩减为零,从而完全去除一些特征。因此,在我们有大量特征的情况下,lasso回归可以很好地进行特征选择,而岭回归只能使系数无穷接近于零,而无法在数学意义上使之绝对为零,即舍弃该特征。关于为什么lasso回归可以进行特征选择,而岭回归不能,详见这篇文章。
传统的方法,如交叉验证,逐步回归来处理过拟合和进行特征选择,对于小的特征集来说效果很好,但当我们处理大的特征集时,以上技术是一个很好的选择。
此外,你也能使用dropout技术,其中心思想是随机的舍弃一些特征,关于dropout,我们后面会单独出一篇文章介绍。