图简介

• 图是网络结构的抽象模型，是一组由边连接的节点
• 图可以表示任何二元关系，例如： 道路、航班
• js中没有图，可以用Object和Array构建图
• 图的表示法：邻接矩阵、邻接表、关联矩阵...

邻接矩阵

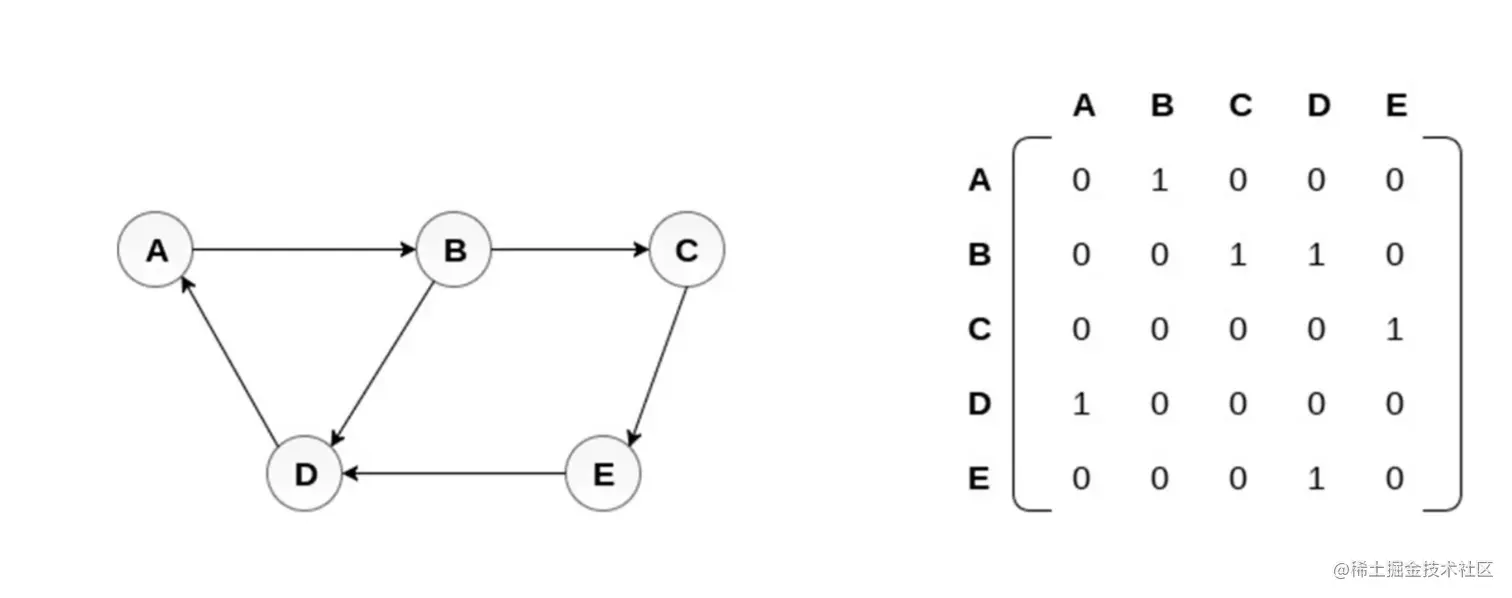
邻接表

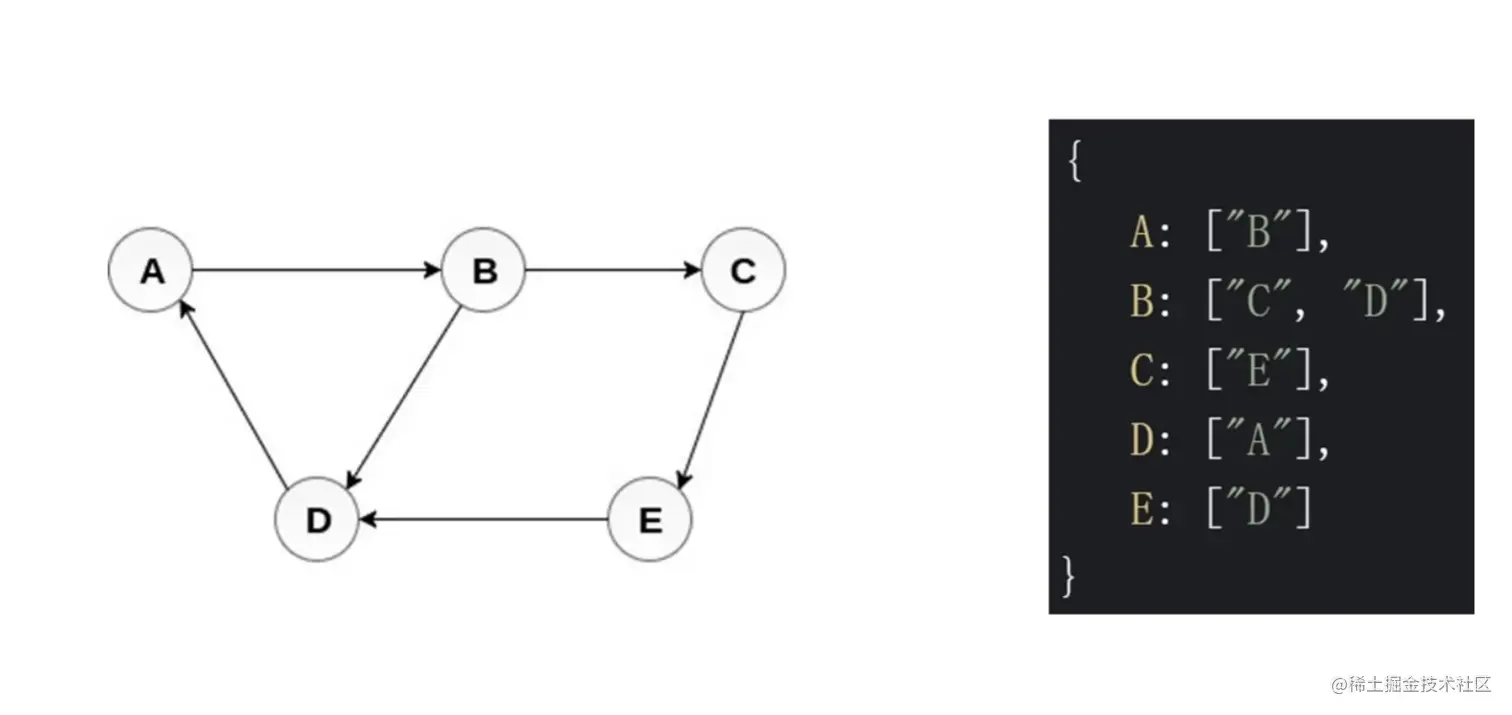
图的常用操作

• 深度优先遍历
• 广度优先遍历

深度优先遍历算法口诀

• 访问根节点
• 对根节点的没有访问过的相邻节点挨个进行深度优先遍历

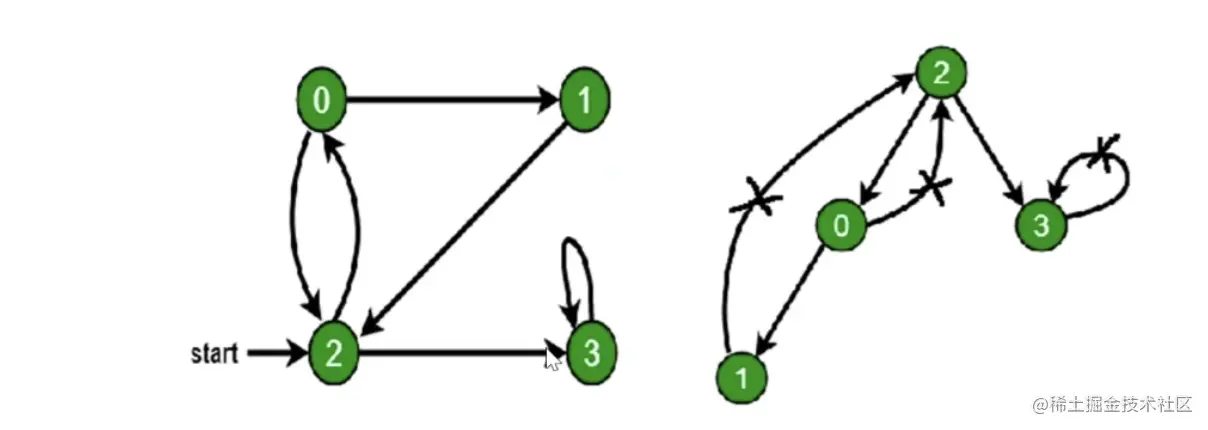
const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3],
};
// 2 0 1 3
const visited = new Set();
const dfs = (n) => {
  console.log(n);
  visited.add(n);
  graph[n].forEach((c) => {
    if (!visited.has(c)) {
      dfs(c);
    }
  });
};
dfs(2);

广度优先遍历算法口诀

• 新建一个队列，把根节点入队
• 把队头出队并访问
• 把队列的没访问过的相邻节点入队
• 重复第二、三步，直到队列为空

const graph = {
  0: [1, 2],
  1: [2],
  2: [0, 3],
  3: [3],
};
// 2 0 3 1
const visited = new Set();
visited.add(2);
const q = [2];
while (q.length) {
  const n = q.shift();
  console.log(n);
  graph[n].forEach((c) => {
    if (!visited.has(c)) {
      q.push(c);
      visited.add(c);
    }
  });
}

leetcode-cn.com 算法题实战

完整题目请打开 leetcode

65.有效的数字

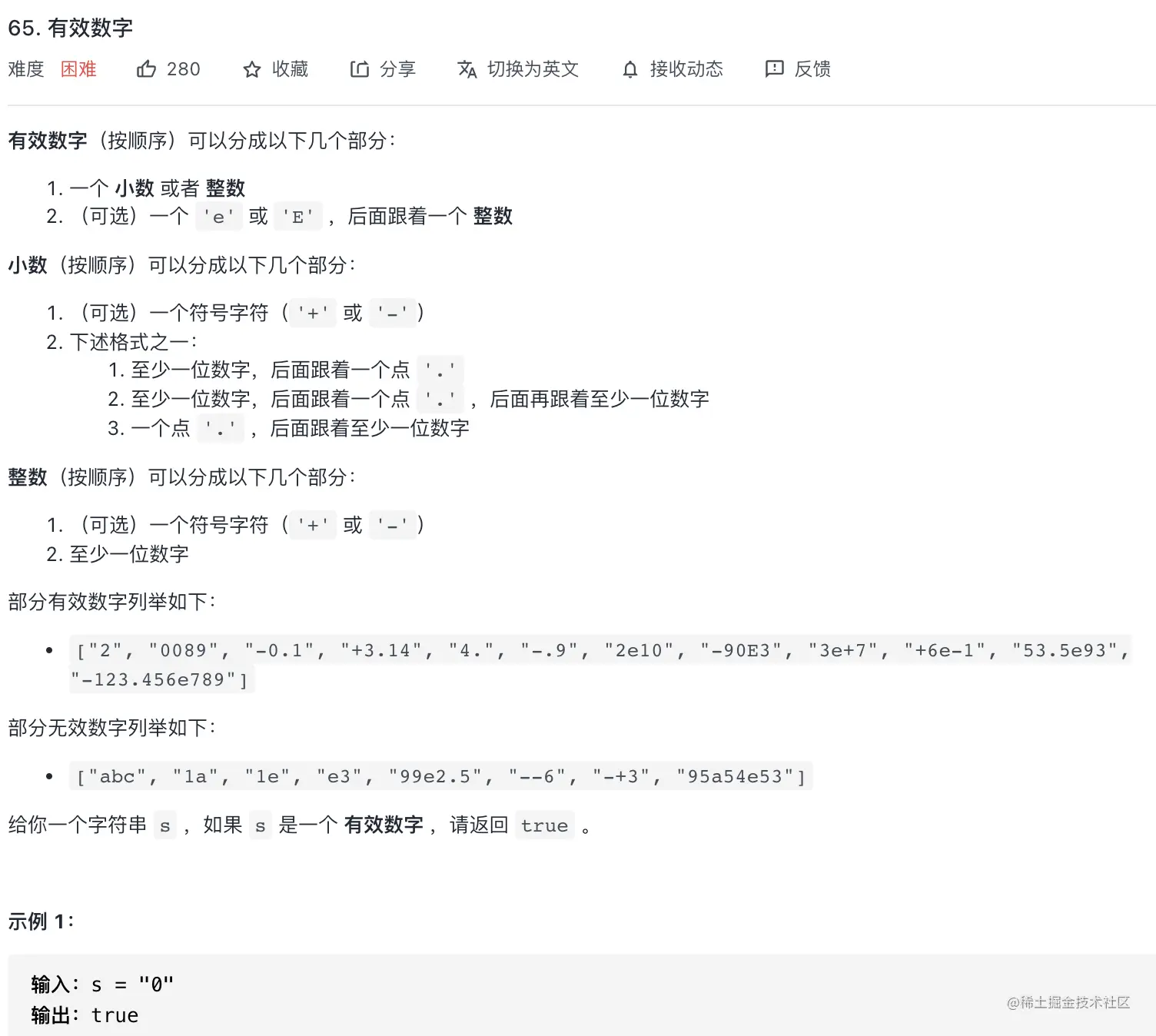
解题思路

• 构建一个表示状态的图。
• 遍历字符串，并沿着图走，如果到了某个节点无路可走就返回 false

/**
 * @param {string} s
 * @return {boolean}
 */
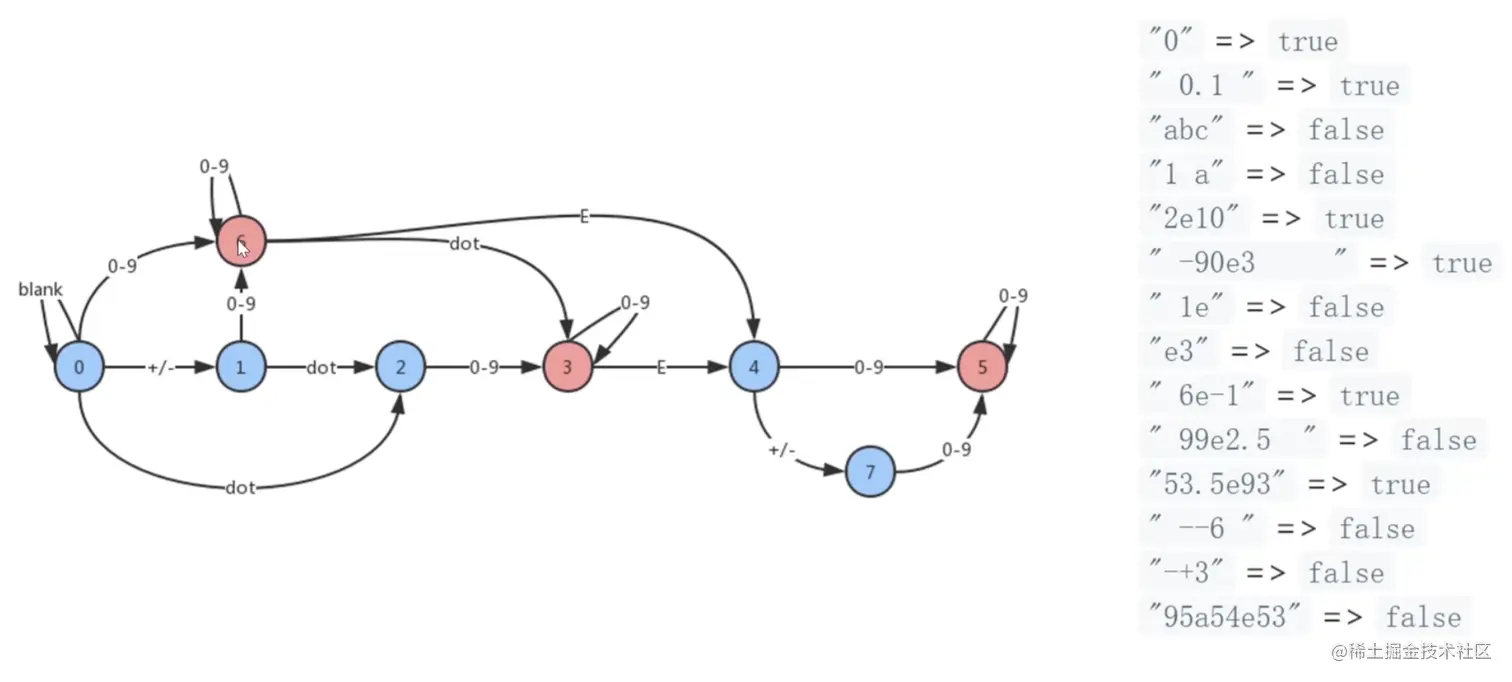
var isNumber = function (s) {
  const graph = {
    0: { blank: 0, sign: 1, ".": 2, digit: 6 },
    1: { digit: 6, ".": 2 },
    2: { digit: 3 },
    3: { digit: 3, e: 4 },
    4: { digit: 5, sign: 7 },
    5: { digit: 5 },
    6: { digit: 6, ".": 3, e: 4 },
    7: { digit: 5 },
  };
  let state = 0;
  for (c of s.trim()) {
    c = c.toLocaleLowerCase();
    if (c >= "0" && c <= "9") {
      c = "digit";
    } else if (c === " ") {
      c = "blank";
    } else if (c === "+" || c === "-") {
      c = "sign";
    }
    state = graph[state][c];
    if (state === undefined) {
      return false;
    }
  }
  if (state === 3 || state === 5 || state === 6) {
    return true;
  }
  return false;
};

下一站 堆