感知机是什么

感知机(Perceptron)

• 输入为实例的特征向量，输出为实例的类别，取+1和-1；
• 感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型；
• 导入基于误分类的损失函数；
• 利用梯度下降法对损失函数进行极小化；
• 感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式；
• 1957年由Rosenblatt提出，是神经网络与支持向量机的基础。

感知机模型

定义:

• 假设输入空间(特征空间)是 X $\subseteq R^n$ ，输出空间是：Y={+1, -1}
• 输入x $\in$ X 表示实例的特征向量，对应于输入空间（特征空间）的点，输出y $\in$ Y,表示实例的类别，由输入空间到输出空间的函数：

$f(x) = sign(w*x + b)$

称为感知机

• 模型参数：w x，内积，权值向量，偏置， 符号函数： $sign(x) = \begin{cases} +1 \qquad x >=0 \\ -1 \qquad x < 0\end{cases}$

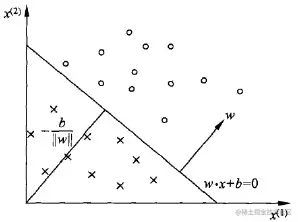
感知机几何解释：

线性方程：$w*x + b = 0$

对应于超平面S，w为法向量，b截距，分离正、负类：分离超平面：

感知机学习策略

如何定义损失函数？

自然选择：误分类点的数目，但损失函数不是w,b 连续可导，不宜优化。

另一选择：误分类点到超平面的总距离：

距离：$\frac {1} {||w||} |w*x + b| > 0$

误分类点： $-y_i (w*x + b)$

误分类点距离： $-\frac {1} {||w||} |w*x + b| > 0$

总距离：

损失函数：

感知机学习算法

Min(w, b) = -\sum_{x\in M} y_i (w*x + b)

随机梯度下降法，

首先任意选择一个超平面，w，b，然后不断极小化目标函数,损失函数L的梯度：

选取误分类点更新：