神经元模型
神经网络中最基本的成分是神经元(neuron)模型,下图展示了M-P神经元模型,其原理是神经元接收到来自其他n个神经元传递过来的输入信号,输入信号通过带权重的连接(connection)来传递,当前神经元根据接收到的信号和权重计算总输入值,将总输入值和阈值θ进行对比,通过激活函数(activation function)来处理神经元的输出。
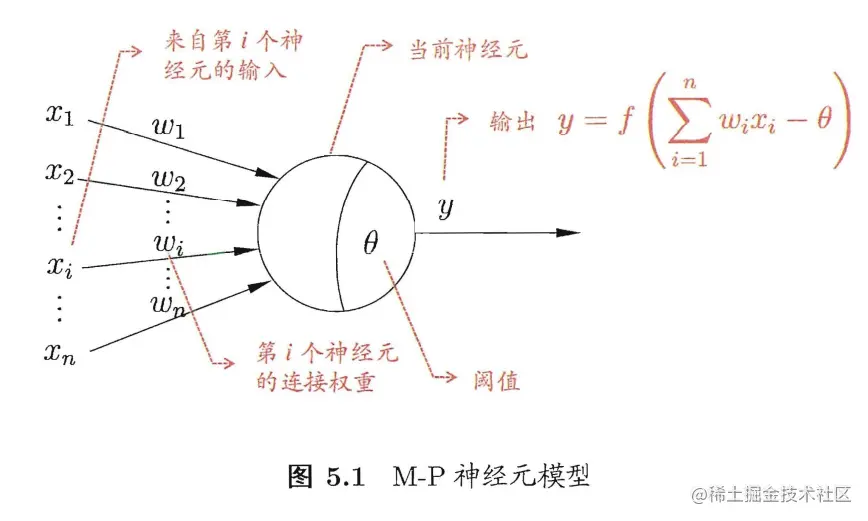
理想的激活函数如下图(a)所示的阶跃函数,对应神经元的两种状态(即有没有超过阈值),但由于其具有不连续不光滑的性质,实际中会使用Sigmoid函数来替代,如下图(b)所示。
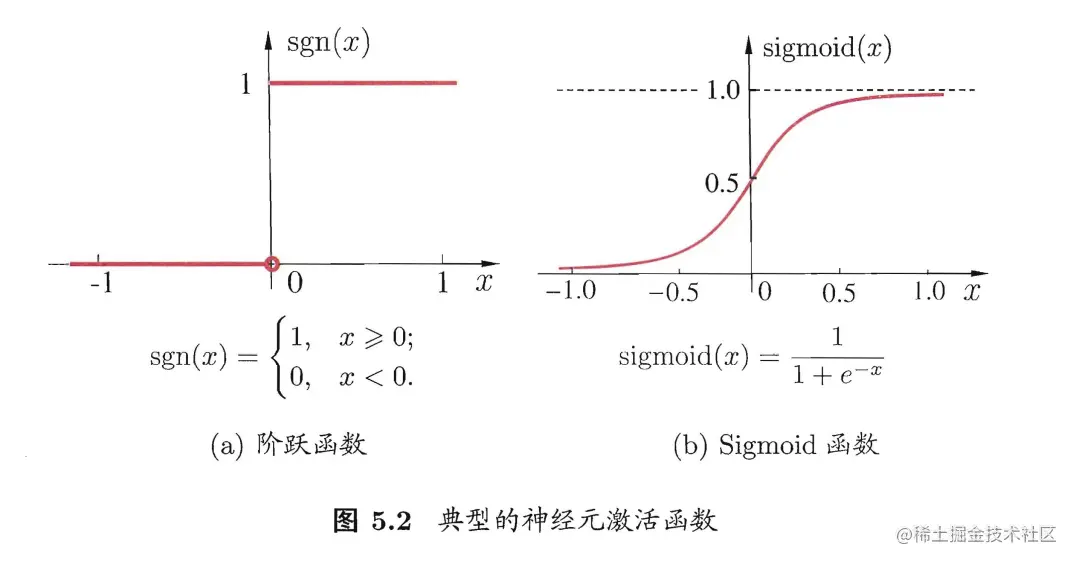
Perceptron 感知机与多层网络
感知机由两层神经元组成,如下图所示,输入层接收到外景输入信号后传递给输出层,输出层为M-P神经元(阔值逻辑单元,threshold logic unit)。
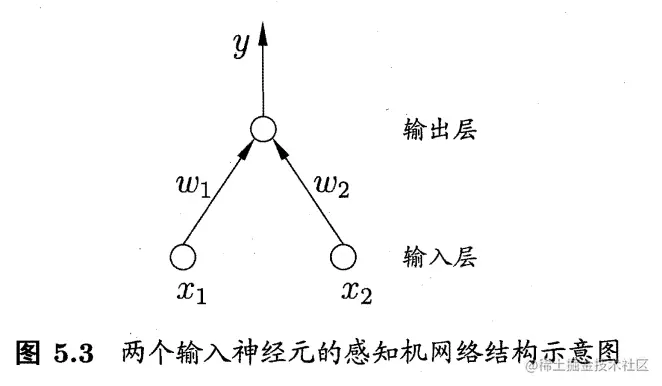
感知机能够简单实现与、或和非的运算(假设y=f(∑iwixi−θ),f为跃迁函数):
- 与运算:令w1=w2=1,θ=2,y(1∗x1+1∗x2−2)仅在x1=x2=1时有y=1;
- 或运算:令w1=w2=1,θ=0.5,y(1∗x1+1∗x2−0.5)当x1=1 or x2=1时有y=1;
- 非运算(仅考虑x1):令w1=−0.6,w2=0,θ=−0.5,y(−0.6∗x1+0∗x2+0.5)当x1=1时y=0,x1=0时y=1。
一般的,给定训练集,可以学习到权重wi(i=1,2,...,n)和阈值θ。θ可看做一个固定输入为-1.0的哑结点(dummy node)所对应连接的权重wn+1,这样权重和阈值两个学习就能统一为单一的权重学习。
对训练样本(xx,y),若当前感知机输出为y^,则其权重按照下式进行调整:
wi←wi+ΔwiΔwi=η(y−y^)xi
η∈(0,1)为学习率(learning rate),从上式可以看出若预测正确即y^=y则Δw不发生变化,否则则按照误差程度进行调整。
感知机只有一层功能神经元(即只有输出层函数使用激活函数处理),其学习能力有限,与、或、非问题都是线性可分(linearly separable)的。若一个问题线性可分,则存在一个线性超平面能将不同类分开,如下图所示。这证明感知机最后一定会收敛(converge)求得合适的权重向量ww。不收敛的感知机会发生震荡,如下图(d)所示,这类问题就是“异或”问题或非线性可分问题。
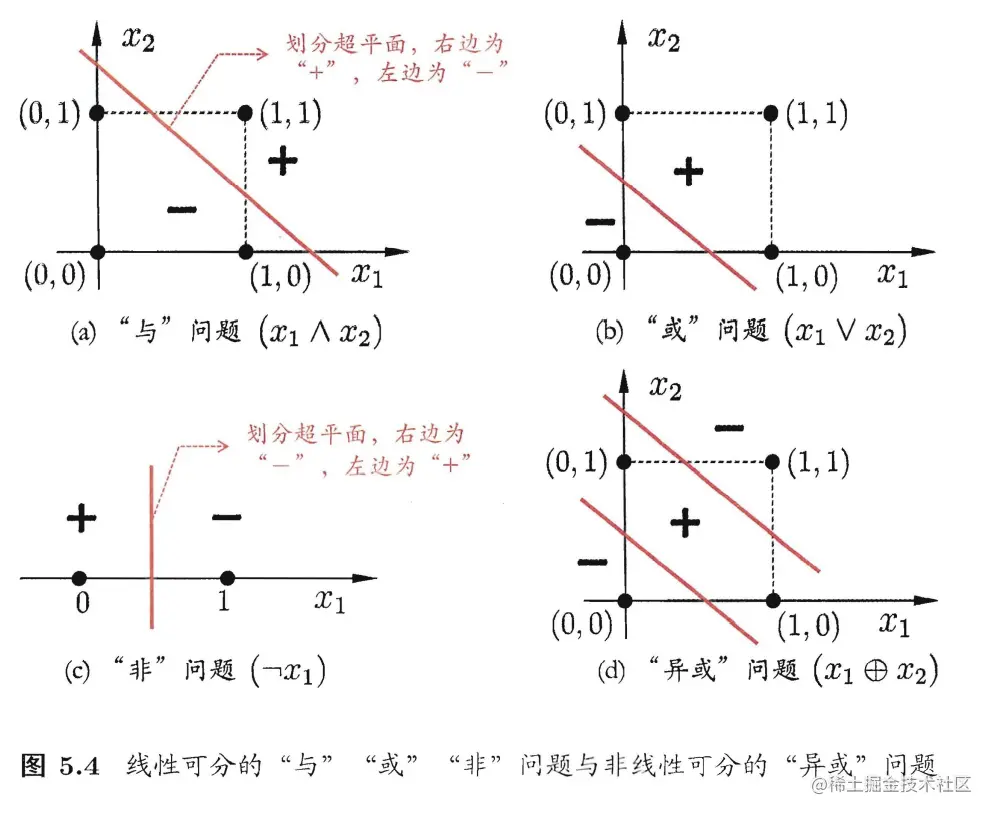
解决非线性可分问题需要考虑使用多层功能神经元,如下图(a)所示,在输入输出层中加入一层神经元称为隐含层(hidden layer),隐含层和输出层都是拥有激活函数的功能神经元。
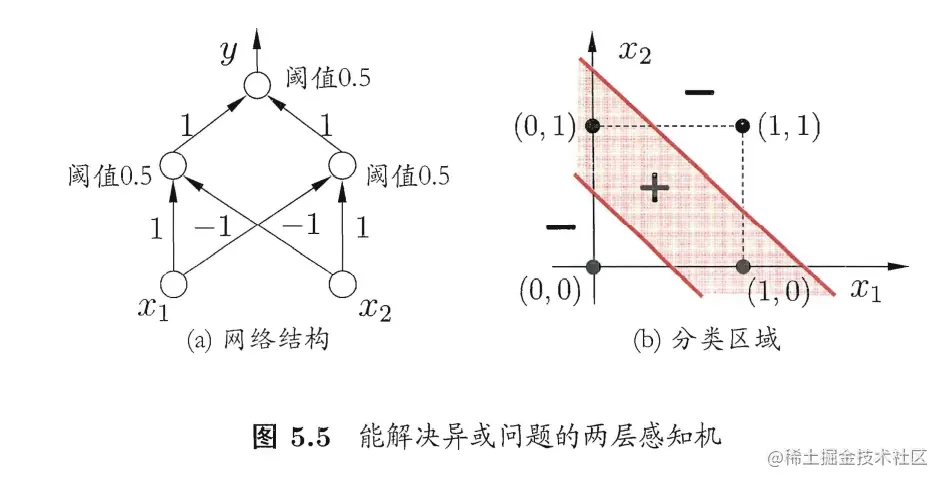
更常见的神经网络是如下图所示的层级结构,每层神经元与下层全部互连,不存在同层或跨层连接,称为多层前馈神经网络(multi-layer feedforward neural networks)。
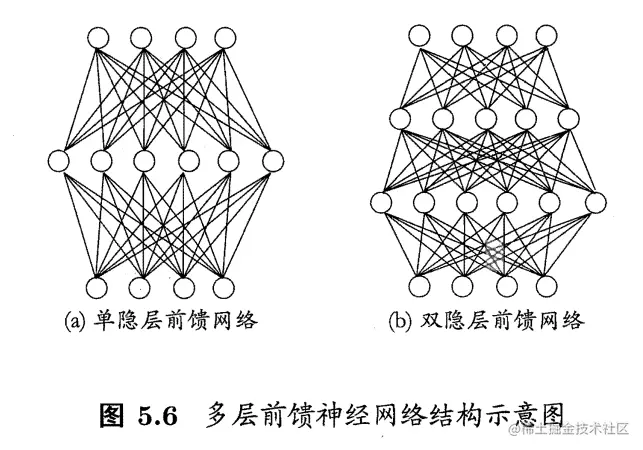
神经网络的学习直观来说就是根据训练数据来调整不同层之间的连接权重(connection weight)ww和每个功能神经元的阈值θ。
error BackPropagation 误差逆传播算法
多层网络的学习能力更强,也需要更复杂的学习算法。误差拟传播(error BackPropagation, BP)算法是最杰出的代表,被广泛应用。BP神经网络一般指用BP算法训练的多层前馈神经网络。
给定数据集D={(xx1,yy1),...,(xxm,yym)},xxi∈Rd,yyi∈Rl。每个输入样本包含d个特征,输出为l维实值向量用于表达分类信息,下图给出了一个多层前馈网络结构。
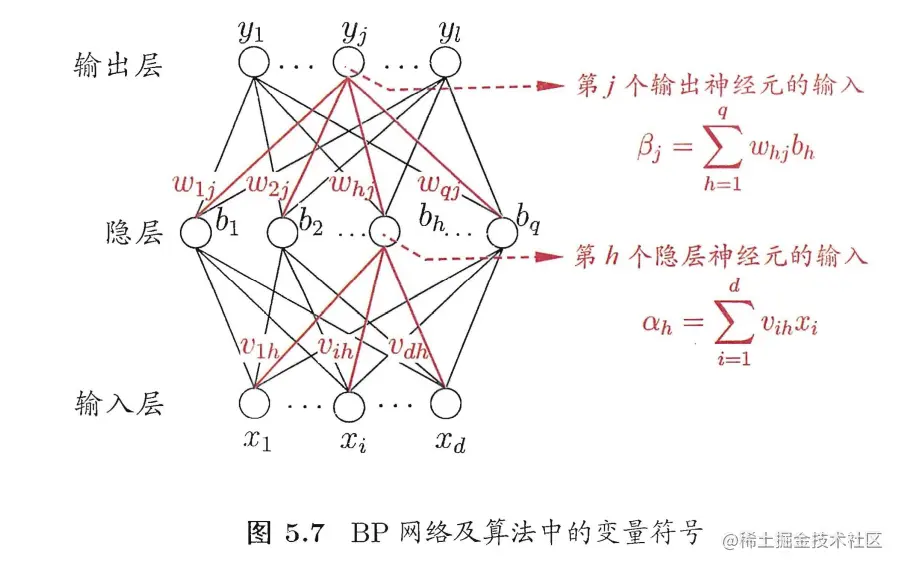
对于训练样本(xxk,yyk),假定神经网络输出为yy^k=(y^1k,...,y^lk),则有:
y^jk=f(βj−θj)
其均方误差为:
Ek=21j=1∑l(y^jk−yjk)2
上图的网络中有(d+l+1)q+l个参数(所有的边+除输入层以外的节点数)需确定,BP是迭代学习算法,每一轮中采用广义的感知学习规则来更新估计参数,任意参数v的更新估计表达式为:
v←v+Δv
以隐含层到输出层的连接权重whj为例,BP算法基于梯度下降(gradient descent)策略,以目标的负梯度方向来调整参数,对于误差Ek和学习率η得到:
Δwhj=−η∂whj∂Ek
whj先影响第j个输出层神经元的输入值βj再影响输出值y^jk最后影响Ek,可得:
∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj
根据βj的定义(可见上图5.7中的βj公式),显然:
∂whj∂βj=bh
其中bh为隐含层第h个神经元的输出。Sigmoid函数有以下性质:
f′(x)=f(x)(1−f(x))
于是可以推出:
gj=−∂y^jk∂Ek⋅∂βj∂y^jk=−(y^jk−yjk)f′(βj−θj)=y^jk(1−y^jk)(yjk−y^jk)
综上可得BP算法中whj的更新公式:
Δwhj=ηgjbh
类似的方法可求出其他参数的更新公式。学习率η控制着算法每一轮迭代的更新步长,若太大容易震荡,太小有可能导致收敛速度过慢。
BP算法的伪码如下所示:

一个案例如下所示:
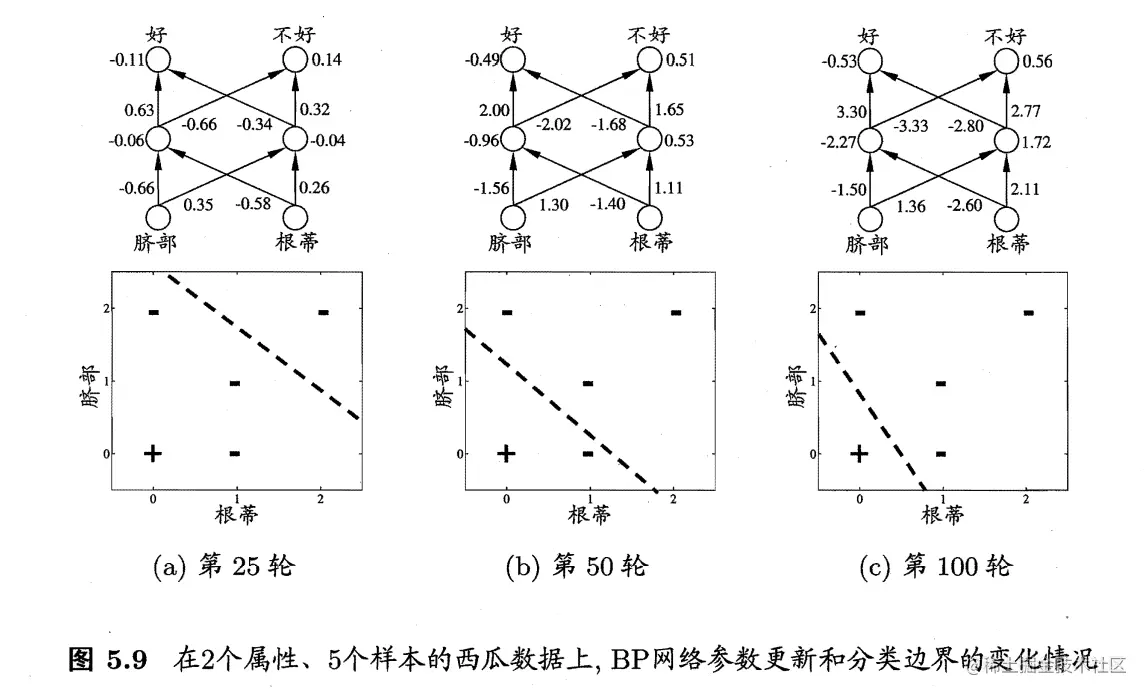
global minimum and local minimum 全局最小和局部极小
神经网络的学习过程其实可以看做为一个参数寻优的过程,“最优”的定义通常有两种:局部极小和全局最小,对于w∗,θ∗,若存在ϵ>0使得:
∀(ww;θ)∈{(ww;θ)∣ ∣∣(ww;θ)−(ww∗;θ∗)∣∣≤ϵ}
- 都有E(ww;θ)≥E(ww∗;θ∗)成立,则(ww∗;θ∗)有局部最小解。
- 若对参数空间中的任意(ww;θ)都有E(ww;θ)≥E(ww∗;θ∗)成立,则(ww∗;θ∗)有全局最小解。
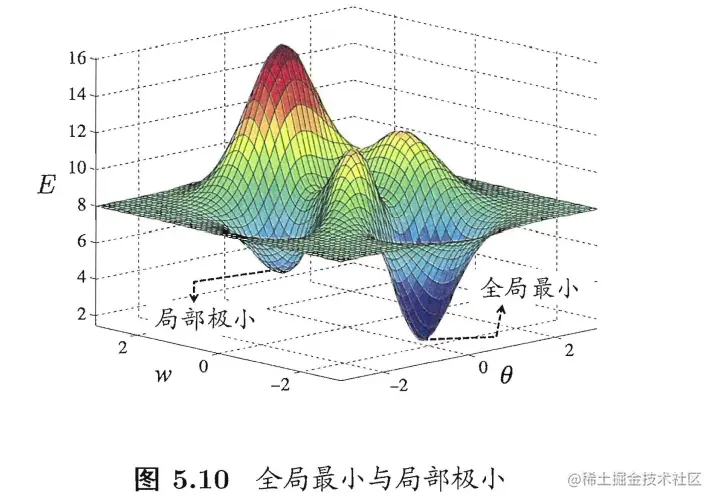
现实任务中人们最希望能找到全局最下值,但有时候误差函数有多个局部最小梯度下降法找到其中一个便停止寻优,这显然不是最优的,因此一些研究者设计了几个策略来试图“跳出”局部极小进而进一步寻找“全局最小”:
- 以多组不同的参数值初始化多个神经网络,训练后取其误差最小的解作为最终参数,这种做法相当于从不同的初始点开始搜索,这样就可能陷入不同的局部最小从而接近全局最小。
- 使用模拟退火(simulated annealing)技术,在每一步迭代中以一定的概率接受比当前解更差的结果(即选择次优解),从而有助于跳出局部最小,接受次优解的概率随着时间推移要逐渐降低从而保持算法的稳定性。
- 使用随机梯度下降,在计算梯度时加入随机因素,让陷入局部最小点时计算的梯度仍可能不为0,从而可以继续搜索。
- 遗传算法(genetic algorithms)。