大厂技术  坚持周更  精选好文

前言

为啥讲数学？

先说下一个时间线：

• 无意间发现了一个宝藏up主3Blue1Brown
• 在看视频的时候，偶然发现一个集合：线性代数的本质。突然想起上学的时候矩阵论（线性代数）老师总说矩阵很优美，但我又一直没get到，所以好奇想看一看。
• 看了一部分觉得很有意思，于是想分享下~
• 但是有没有啥用呢？在评论里看到矩阵是图形学的基础，于是搜了下，发现它比我想的有用多了！只要涉及到图形学，矩阵都是绕不开的，比如webgl等等；
• 但是和我们前端的大部分日常工作关系不大，讲了大家会有兴趣吗？纯讲理论能讲的明白不？于是我突然想到transform里用到了矩阵，是一个合适的实践例子
• 至此，我发现矩阵既有意思，又有意义，又可以有实践例子（transform），于是有了这篇文章。

文中会涉及到一些最基本的矩阵运算，所以需要学过线性代数/矩阵论。只要学过就行，忘记了没关系，提示一下稍微有点印象就行！

讲什么？

几乎所有的学科（理工科）都要学线性代数，比如计算机科学、物理学、电子工程学、机械工程学、统计学等等。我们学习了如何计算矩阵：数乘、叉乘、特征值等，但是也只限于计算，大家会不会有以下几个疑问：

• 这里计算的规则为什么是这么定义的？
• 我们为什么要学这些？
• 学这些有什么实际用处？

我们学的很多课程，大家可能都有这个疑惑，甚至至今也不清楚。对于线性代数，今天分享的目的就是希望能回答这些问题。

线性代数，我们只学了它的计算，但其实更重要的是它的几何含义。计算只是解决问题的工具，而明白其几何含义帮助我们知道解决什么问题要用什么工具，以及如何解读最终结果的含义。

好了废话这么多，主要是想激发大家的兴趣，希望大家不要因为满篇的公式而觉得枯燥，内容其实不复杂也很有意思。当然这建立在我能传达出我想讲的东西，我尽量做到。

本文分为2个部分：

• 一部分：内容来自于宝藏up主的线性代数合集，主要是讲一些基本矩阵运算的几何含义，我按我的理解分享下，更多精彩推荐大家去看原视频
• 二部分：通过transform的矩阵，来消化所讲的内容。

矩阵基本运算

如果直接告诉大家矩阵是如何表示几何意义的，其实这样大部分人也能记住且很好的应用，但是还是希望大家能真正地理解原因，所以先讲一些基础。

向量及基本运算

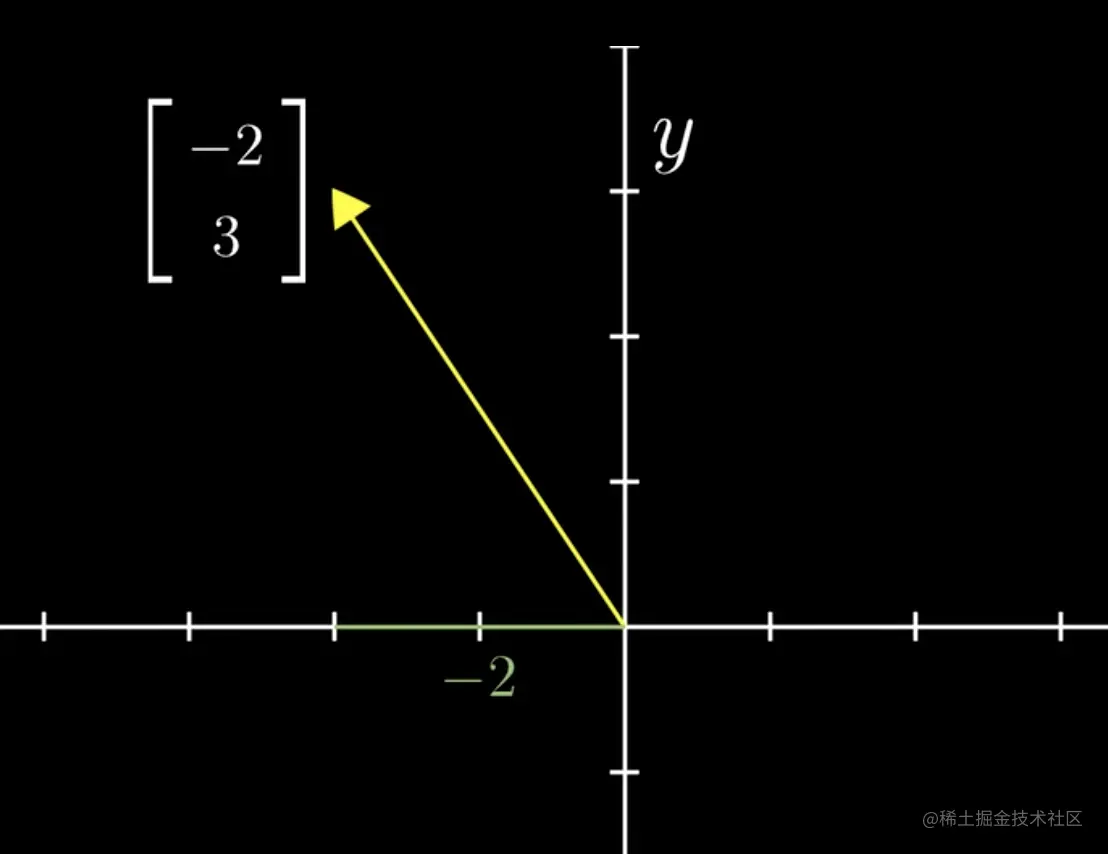
矩阵的基础是向量，我们先来看看向量。向量在不同学科眼里是不同的东西，甚至于它可以是任何东西，只要保证其相加和数乘有意义即可。 为什么只需要相加和数乘，一会下面会说明：只需要这2种运算，就可以到达空间内的任何一点。 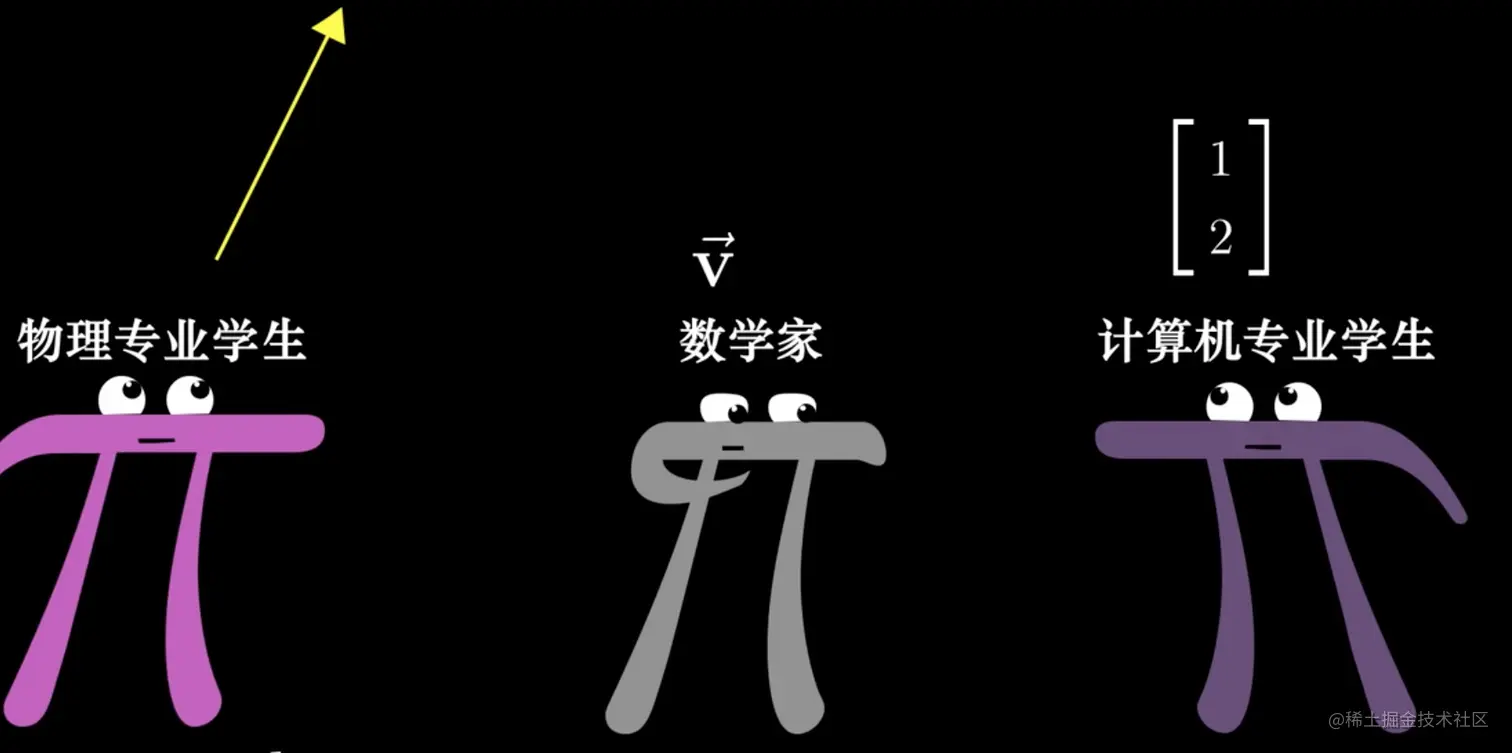一个向量可以表示为$\vec v$、表示为$\begin{bmatrix}-2\\3\\\end{bmatrix}$、表示为坐标系上的一个箭头

相加

• 数学表示$\begin{bmatrix}a\\b\\\end{bmatrix}$+ $\begin{bmatrix}m\\n\\\end{bmatrix}$= $\begin{bmatrix}a+m\\b+n\\\end{bmatrix}$，$\vec v$+$\vec w$= $\vec v+\vec w$。
• 几何表示：

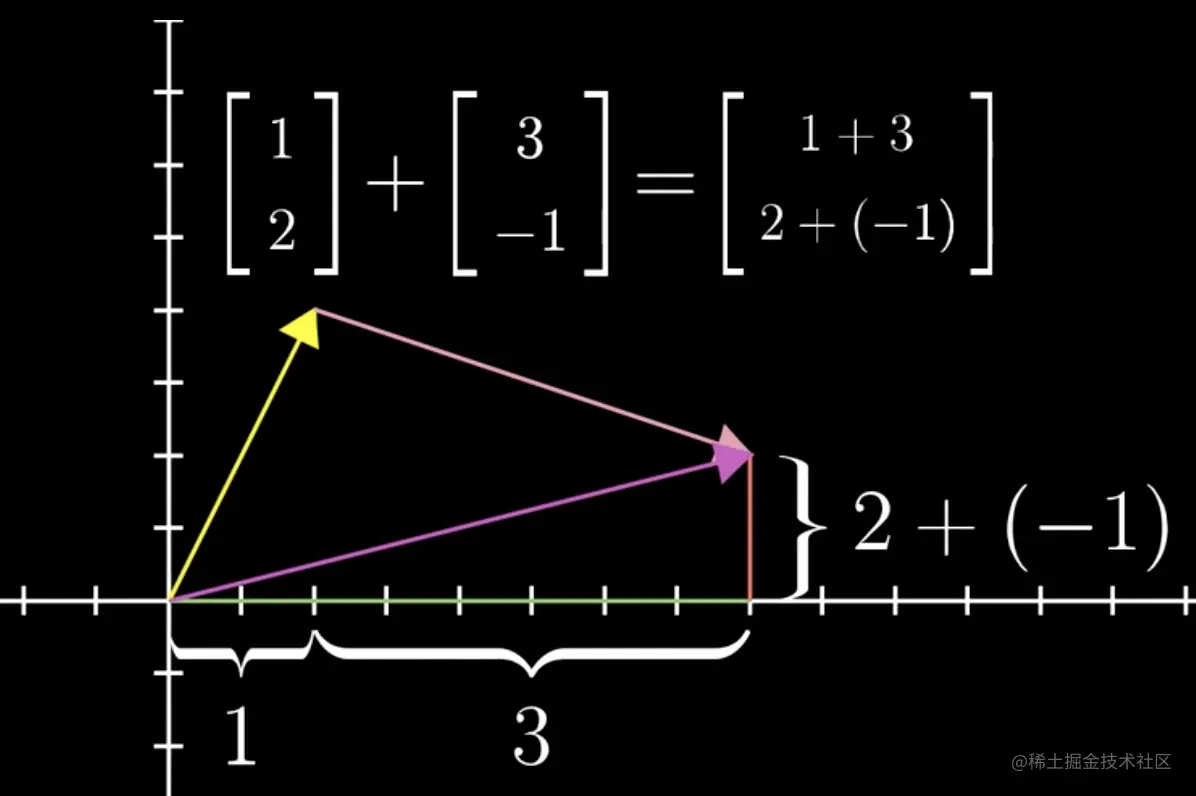
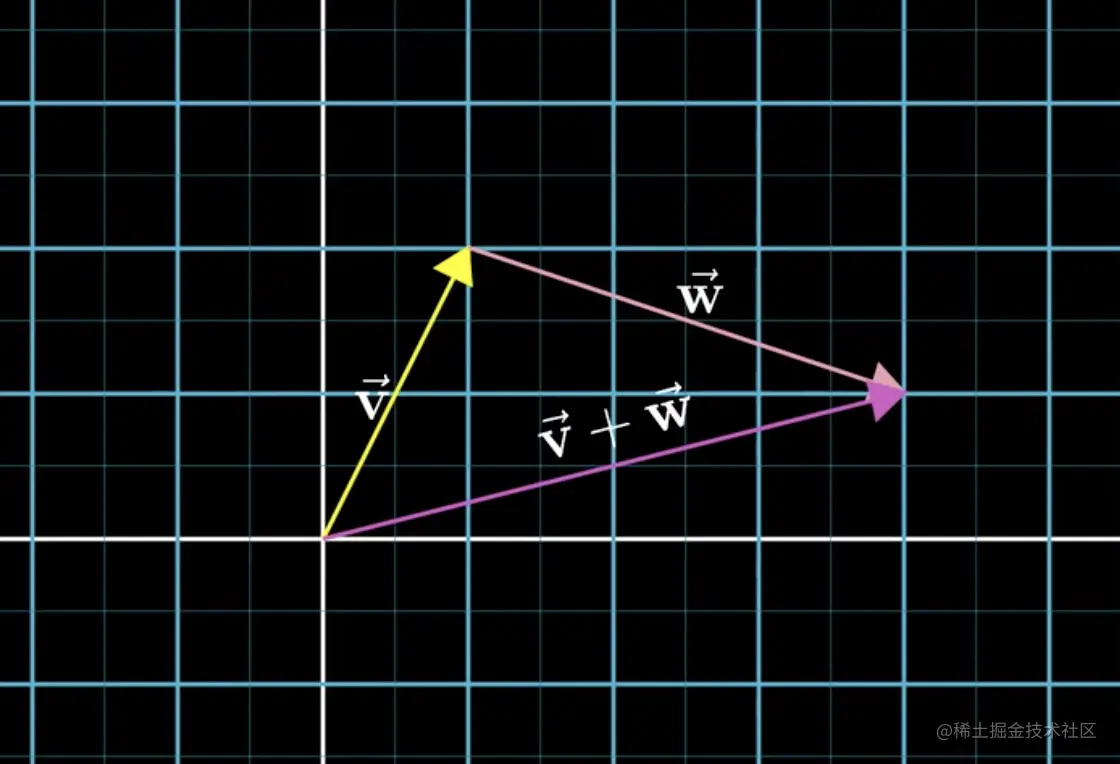将向量看成一个运动，从原点出发，向$\vec v$方向移动长度$\left| \vec v \right|$后，再向$\vec w$方向移动长度$\left| \vec w \right|$后，就等于直接向$\vec v+\vec w$方向移动长度$\left| \vec v+\vec w \right|$。

结合数学和几何的表示，我们就能知道为什么向量的相加要这样定义：$\begin{bmatrix}a\\b\\\end{bmatrix}$+ $\begin{bmatrix}m\\n\\\end{bmatrix}$= $\begin{bmatrix}a+m\\b+n\\\end{bmatrix}$。

数乘

• 数学表示:$m\vec v$=$m\begin{bmatrix}x\\y\\\end{bmatrix}$= $\begin{bmatrix}mx\\my\\\end{bmatrix}$
• 几何表示：

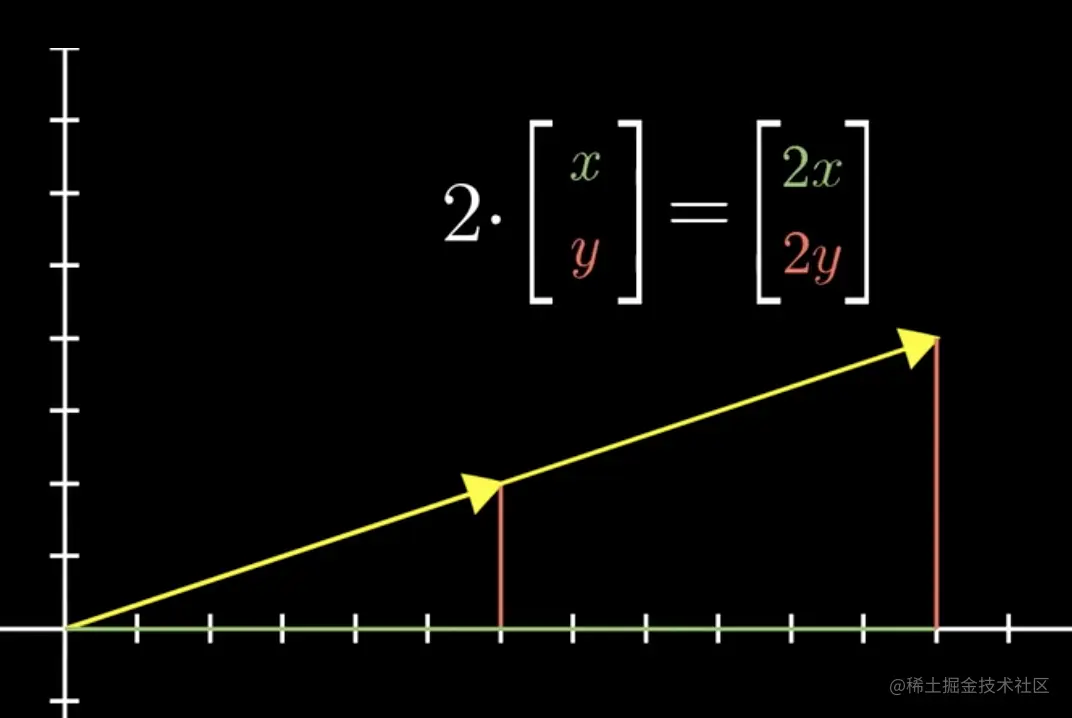将$\vec v$在其方向上延长至2倍，此时也就相当于在x轴和y轴上分贝放大2倍，也就是$m\vec v$=$m\begin{bmatrix}x\\y\\\end{bmatrix}$= $\begin{bmatrix}mx\\my\\\end{bmatrix}$的定义。

线性组合、张成空间与基

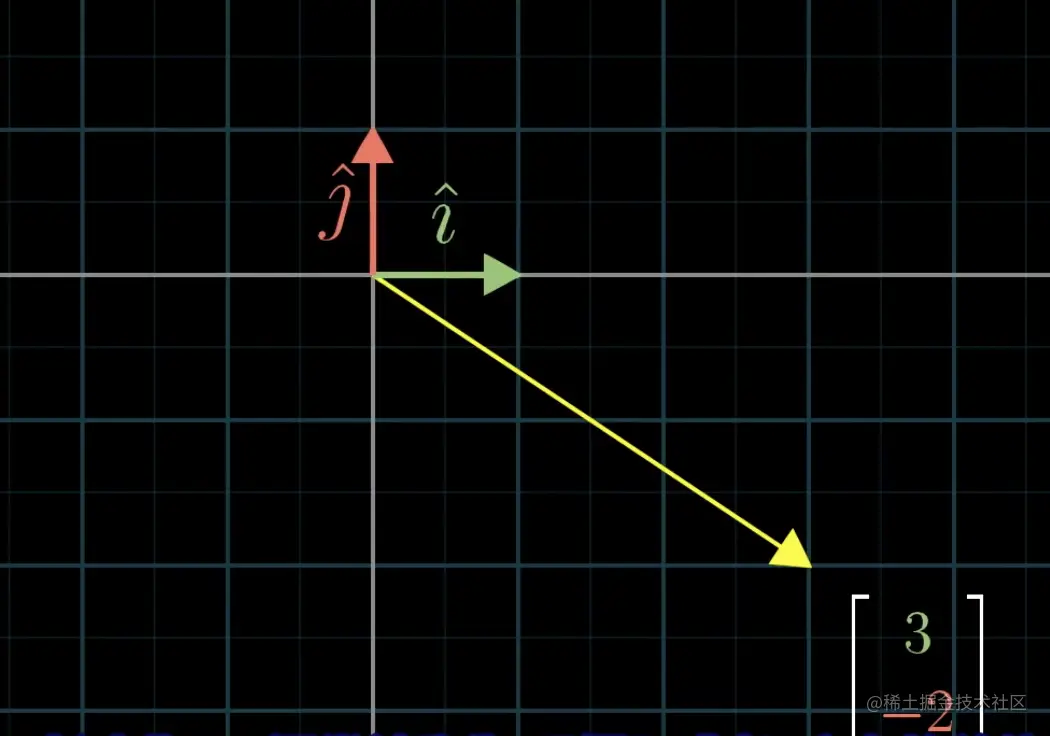
在描述向量时，有一个我们用到了但是没注意的东西：向量的基。我们都是默认了向量的基坐标为平面坐标系上x轴方向上的$\vec i$和y方向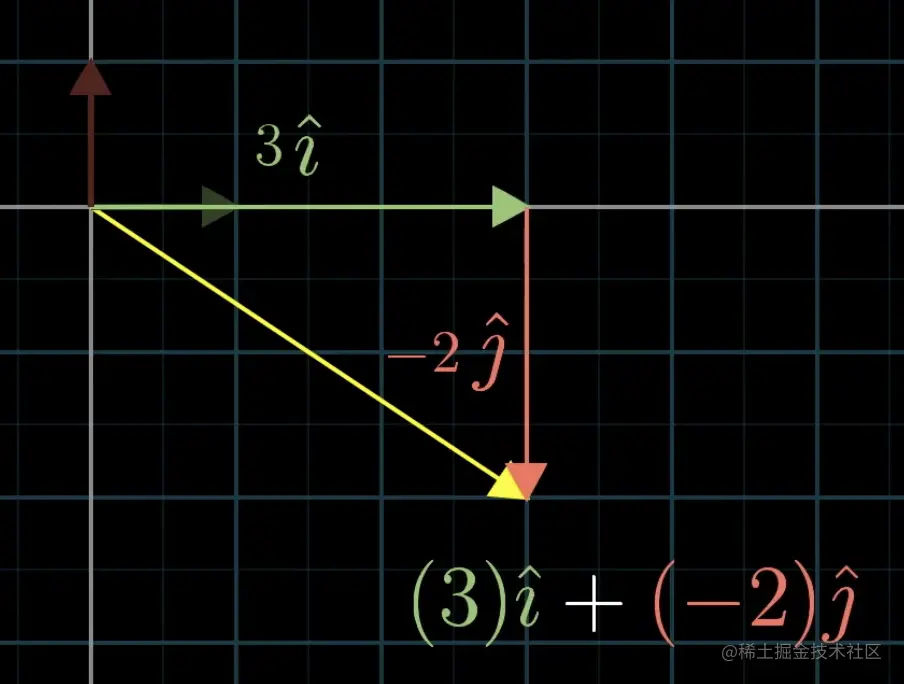上的$\vec j$。 通过这2个基，再利用数乘$m\vec v$和相加$\vec v$+$\vec w$= $\vec v+\vec w$，我们可以得到平面上的任何向量（三维可同理类推），这些向量称为基向量的线性组合，整个二维平面尽在掌握。

那我们改变基坐标，是不是每一对基坐标都可以掌握整个平面呢？ 不是。当2个基向量正好共线时，它们的线性组合永远都只能是一条线；而当2个向量都为零向量时，它们的线性组合永远只能待在原点。（3:17 - 3:58）

www.bilibili.com/video/BV12s…

换成术语，我们将所有可以表示为给基向量线性组合的向量的集合称为给定向量所张成的空间，从刚刚的描述可知，对于大部分二维向量，它们张成的空间是整个二维平面，小部分情况下也可能是一条直线或者一个点。

那我们如何选取基向量呢？

如果一个向量$\vec c$，可以由平面上2个向量$\vec a$和$\vec b$经过数乘和相加得到，那它就不会对张成的空间做出任何贡献，也就是$\vec a$、$\vec b$、$\vec c$中至少有一个是可以去掉的，这时我们就会说a、b、c是线性相关的；而同时我们可以得出结论，空间向量的一组基是张成该空间的一个线性无关的向量集。

到这里我们可以发现，只要通过向量的数乘和相加，我们就可以张成整个对应维度的空间，也就是达到整个对应维度空间内的任意点。 顺便瞧瞧张成的三维空间 （7:49 - 8:09）

www.bilibili.com/video/BV12s…

矩阵和线性变换

以上向量是基础运算，一切都是为了更好的理解矩阵运算。

很遗憾，矩阵是什么是说不清的，你必须得自己看看。——墨菲斯

函数是将一个输入经过一些处理变为一个输出，如y=f(x)。那向量的运算a=L(b)也是如此，为什么我们不把向量的运算叫函数，而都是叫向量变换/矩阵变换呢。这提醒我们要用运动的思想看待向量的计算，或者换一种说法，矩阵/向量变换是对空间的变换。

说明一点，比函数稍微简单的是，矩阵变化都是线性变换（因为都是依赖向量数乘和相加）。

• 原点不动
• 直线依然是直线

线性变换是使得网格线平行且等距的变换。 （2:39 - 3:51）

www.bilibili.com/video/BV1ns…

视频中提到一个问题：对于平面上的一个输入$\vec b$，我们该给计算机一个什么公式L，才能得到 $\vec a$=L($\vec b$)呢？

按上面讲到的，$\vec i$和$\vec j$是张成二维平面的最简单的一对基，因此以下关注对二维平面的变换时，只需要关注这对基的线性变换，我们就可以得到整个平面的线性变换，也就是公式L。

比如，$\vec i$变为$\begin{bmatrix}2\\1\\\end{bmatrix}$，$\vec j$变为$\begin{bmatrix}3\\-2\\\end{bmatrix}$，整个二维平面就发生了如下变化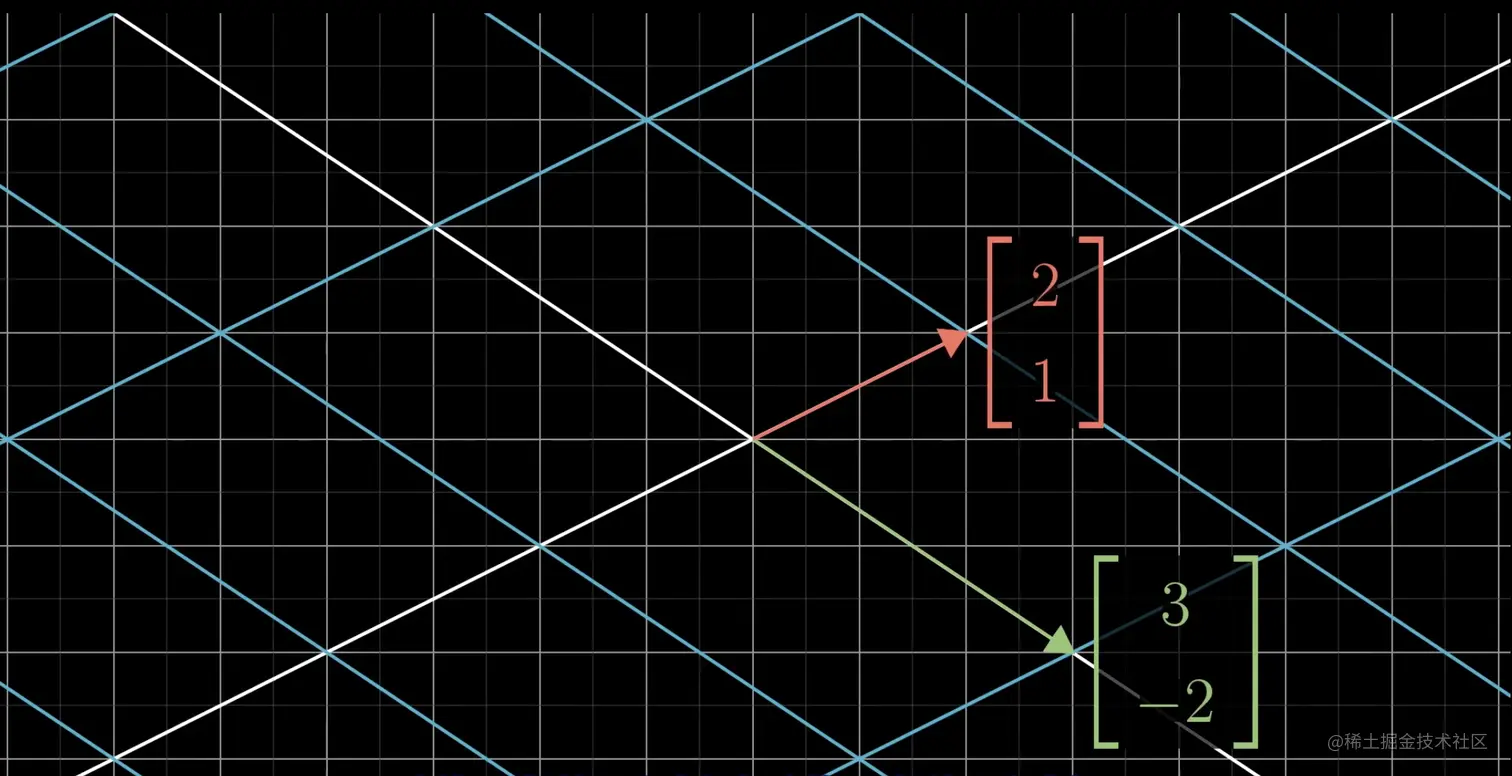： 我们将变化后的2个基向量按如下方式放入矩阵，这样这个矩阵 $\begin{bmatrix}3&2\\-2&1\\\end{bmatrix}$就表示了一次对二维空间的变换，也就是公式L，其中的2列分别为经过变换后的$\vec i$和$\vec j$。

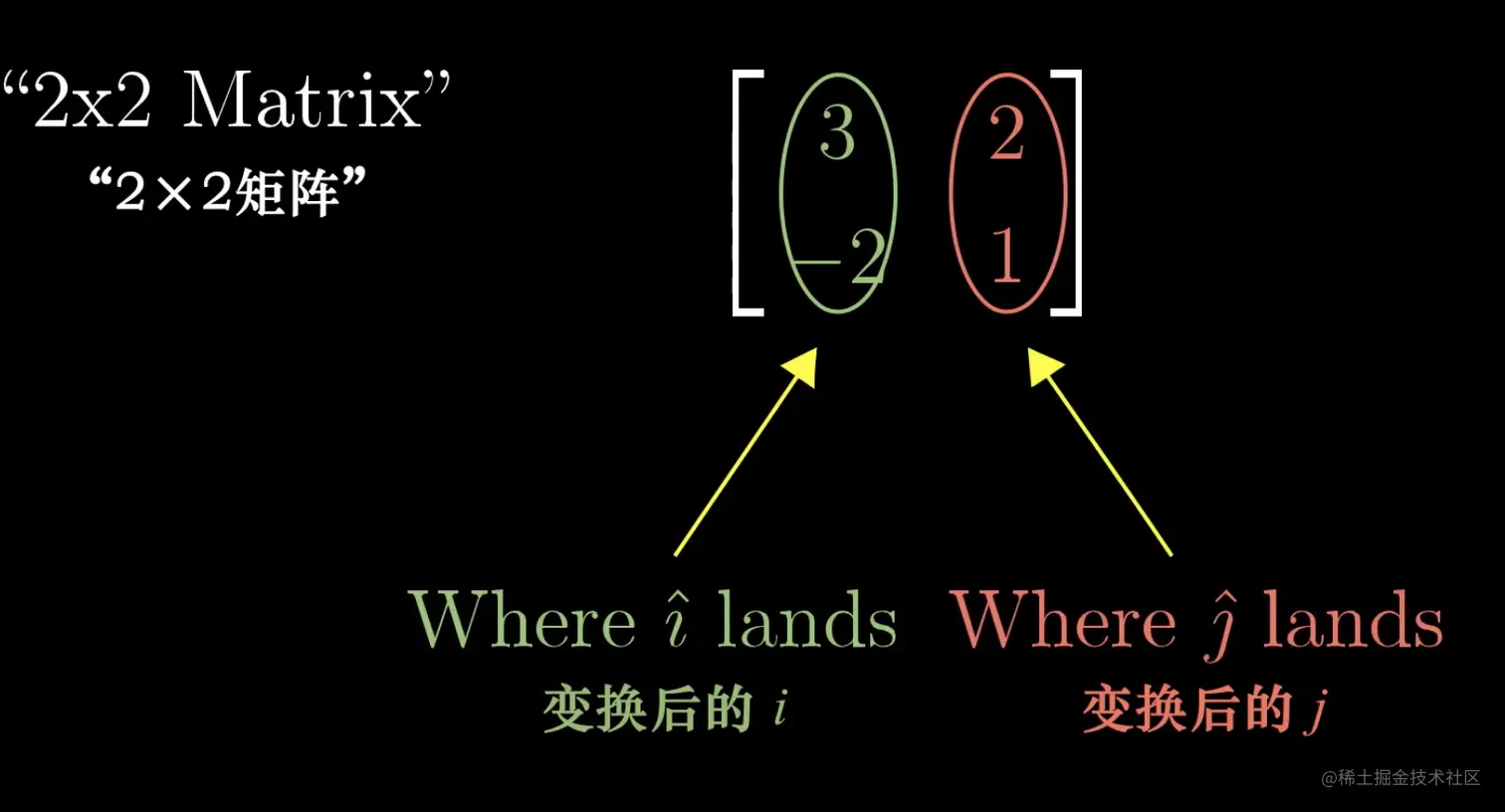
矩阵向量相乘

理解一个【矩阵是一次对空间的变换，且其中2列分别为经过变换后的基向量$\vec i$和$\vec j$】这一点至关重要，这是理解所有后续操作的基础。

现在，我们回答上面的问题：如果你想知道一个向量$\vec b$，比如$\begin{bmatrix}5\\7\\\end{bmatrix}$，经过线性变化后的位置，也就是L($\vec b$)的位置，则只需要计算$5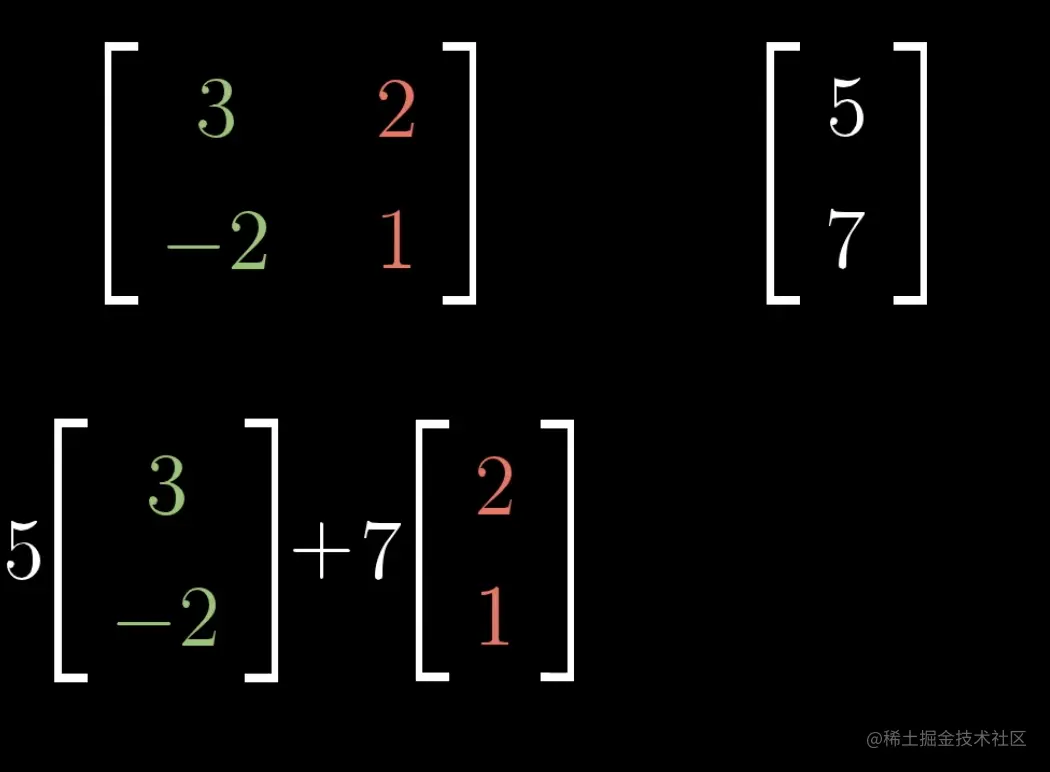\vec i$+$7\vec j$=$5\begin{bmatrix}3\\-2\\\end{bmatrix}$+$7\begin{bmatrix}2\\1\\\end{bmatrix}$即可。 抽象后 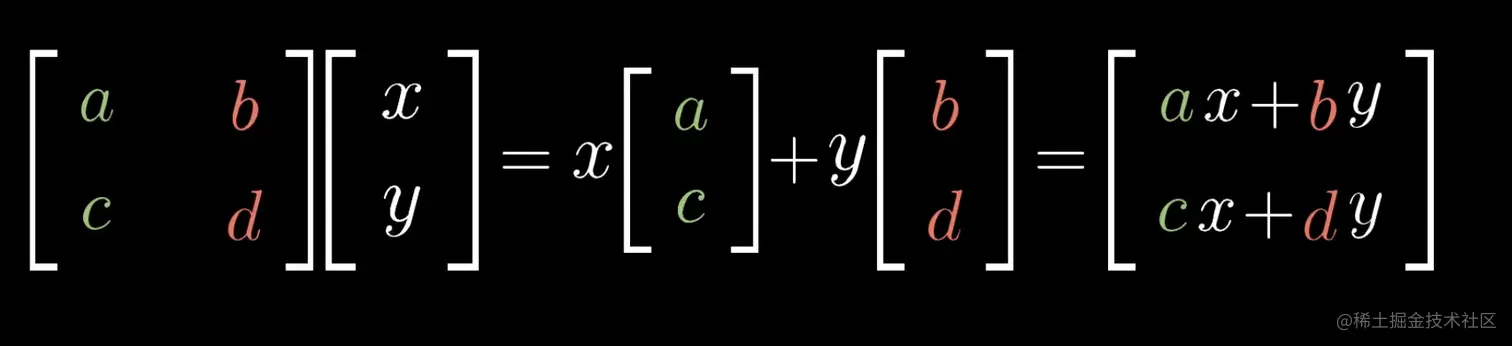停下来体会下.....

以上其实我们就得到了矩阵向量向量相乘的几何意义：一个向量 $\begin{bmatrix}x\\y\\\end{bmatrix}$ 左乘一个矩阵$\mathbf{A}$得到的值的几何意义是：这个向量在新的空间（经过矩阵$\mathbf{A}$变换后的空间）里的位置。

矩阵乘法

矩阵是对一个空间的变换，那如果我们想相继对空间进行多次变换呢？

此时，我们就不一步步描述一个具体的向量$\begin{bmatrix}x\\y\end{bmatrix}$的去向，直接描述整个平面的变换，更具体的过程大家可以去看看视频。

我们先对平面进行一个 $\mathbf{M{_1}}$=$\begin{bmatrix}e&f\\g&h\\\end{bmatrix}$ 变换：$\vec i$变换至$\begin{bmatrix}e\\g\\\end{bmatrix}$，$\vec j$变换至$\begin{bmatrix}f\\h\\\end{bmatrix}$，然后进行一个$\mathbf{M{_2}}$=$\begin{bmatrix}a&b\\c&d\\\end{bmatrix}$变换。

此时$\vec i$将变换为$\mathbf{M{_2}}\vec i=\begin{bmatrix}a&b\\c&d\\\end{bmatrix}\vec i= \begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}e\\g\\\end{bmatrix}=e\begin{bmatrix}a\\c\\\end{bmatrix}+ g\begin{bmatrix}b\\d\\\end{bmatrix}=\begin{bmatrix}ae+bg\\ce+dg\\\end{bmatrix}$

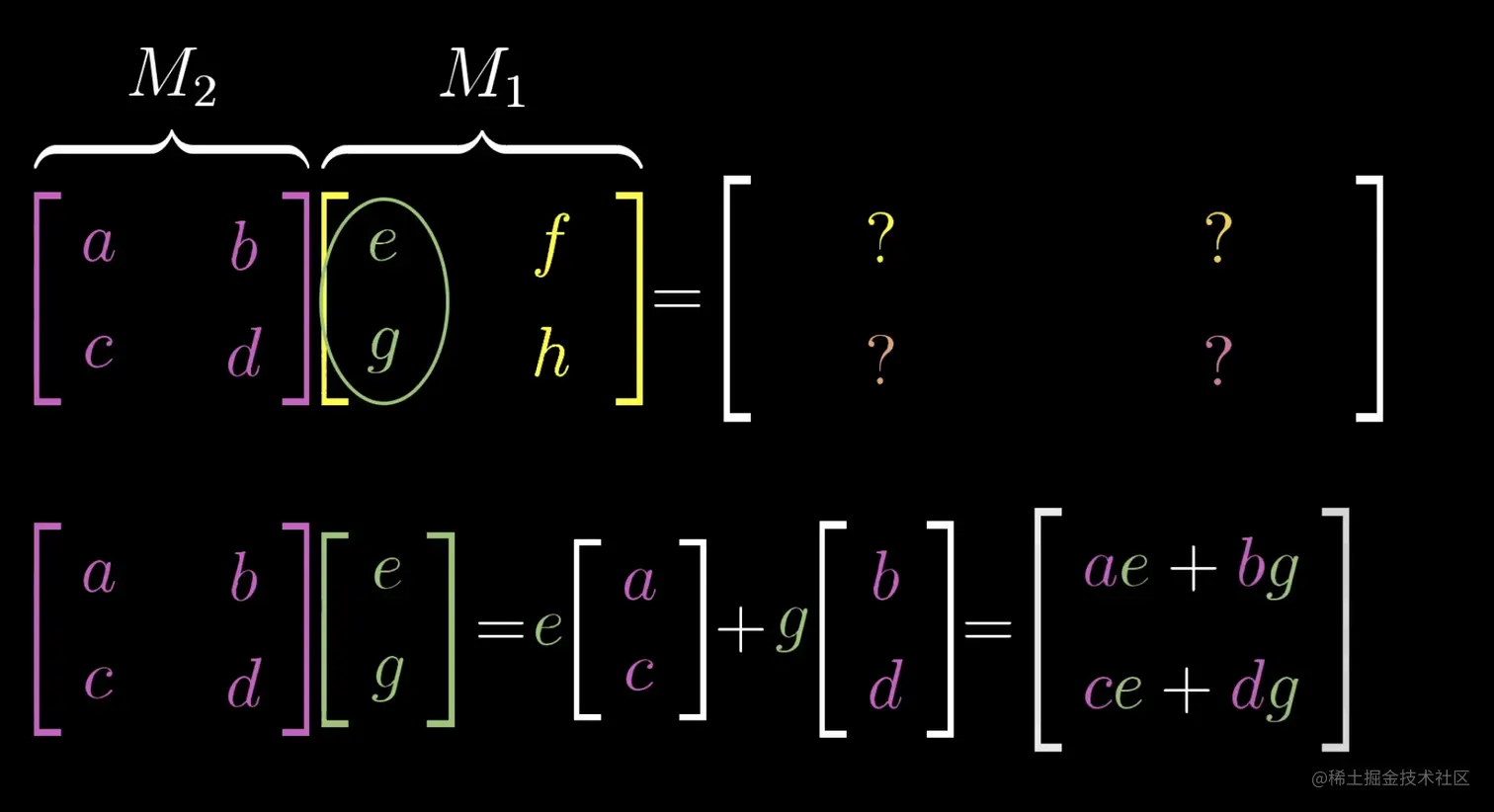
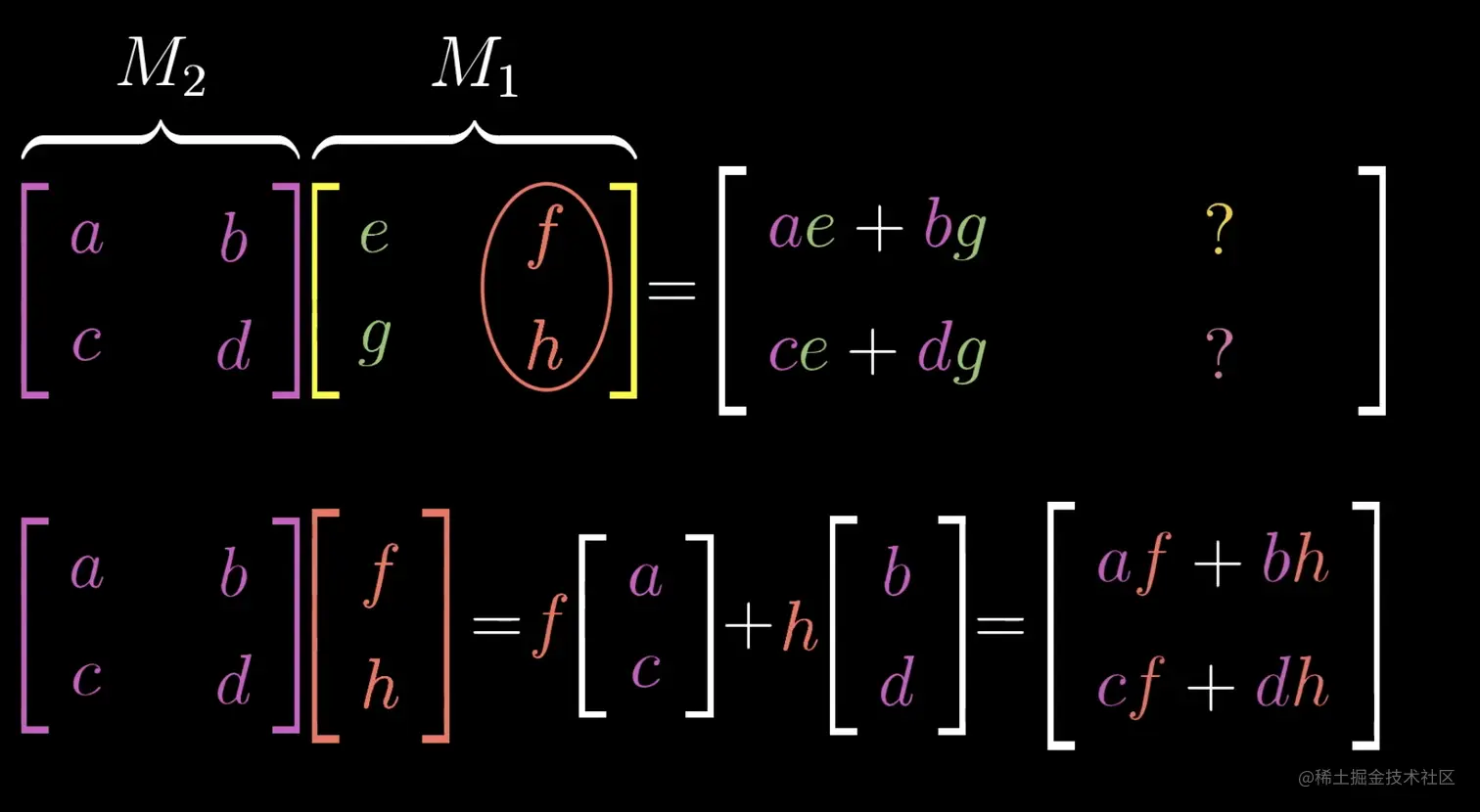此时$\vec j$将变换为$\mathbf{M{_2}} \vec j= \begin{bmatrix}a&b\\c&d\\\end{bmatrix}\vec j= \begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}f\\h\\\end{bmatrix} = f\begin{bmatrix}a\\c\\\end{bmatrix}+ h\begin{bmatrix}b\\d\\\end{bmatrix}=\begin{bmatrix}af+bh\\cf+dh\\\end{bmatrix}$ 以上的过程也就得到了矩阵的乘法定义，即

$\mathbf{M{_2}} \mathbf{M{_1}}= \begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}e&f\\g&h\\\end{bmatrix}=\begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}e\\g\\\end{bmatrix}+\begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}f\\h\\\end{bmatrix}=\begin{bmatrix}ae+bg&af+bh\\ce+dg&cf+dh\\\end{bmatrix}$

以上整个过程，我们学习矩阵乘法时都是直接背下来的，而明白了它的几何意义后，希望大家可以每次在用到的时候思考下其背后的几何意义——对空间的多次相继变换，这样对矩阵会有一个更好的认识。

乘法结合律和交换律

如果大家还有点印象的话，矩阵是满足乘法结合律，而不满足乘法交换律的。为什么是这样呢？通过几何意义，我们可以很好地理解原因。

• 结合律：$\mathbf{M{_3}}\mathbf{M{_2}} \mathbf{M{_1}}$?= $\mathbf{M{_3}}(\mathbf{M{_2}} \mathbf{M{_1}} )$

等式左边表示：先进行$\mathbf{M{_1}}$变换，再进行$\mathbf{M{_2}}$变换，再进行$\mathbf{M{_3}}$变换

等式右边表示：先进行$\mathbf{M{_1}}$变换，再进行$\mathbf{M{_2}}$变换，(等一会儿？)再进行$\mathbf{M{_3}}$变换

是不是发现没有任何差别，甚至于不需要证明，显而易见。

• 交换律：$\mathbf{M{_2}} \mathbf{M{_1}}$?= $\mathbf{M{_1}} \mathbf{M{_2}}$

等式左边表示：先进行$\mathbf{M{_1}}$变换，再进行$\mathbf{M{_2}}$变换

等式左边表示：先进行$\mathbf{M{_2}}$变换，再进行$\mathbf{M{_1}}$变换

文字不好描述，我们来看看视频 （7:38 - 8:13）

www.bilibili.com/video/BV1ms…

这一过程我们无需数值证明，只需要在脑海里想象一下，就可以知道交换律不成立，也就是空间变换的顺序不是随意的。当然，数值计算下也可以很简单的得出这一结论：

$\mathbf{M{_2}} \mathbf{M{_1}}= \begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}e&f\\g&h\\\end{bmatrix}= \begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}e\\g\\\end{bmatrix}+\begin{bmatrix}a&b\\c&d\\\end{bmatrix}\begin{bmatrix}f\\h\\\end{bmatrix}=\begin{bmatrix}ae+bg&af+bh\\ce+dg&cf+dh\\\end{bmatrix}$

$\mathbf{M{_1}} \mathbf{M{_2}}= \begin{bmatrix}e&f\\g&h\\\end{bmatrix}\begin{bmatrix}a&b\\c&d\\\end{bmatrix}= \begin{bmatrix}e&f\\g&h\\\end{bmatrix}\begin{bmatrix}a\\c\\\end{bmatrix} +\begin{bmatrix}e&f\\g&h\\\end{bmatrix}\begin{bmatrix}b\\d\\\end{bmatrix}=\begin{bmatrix}ea+cf&eb+dh\\ga+hc&eb+gd\\\end{bmatrix}$

很明显两者不相等，大家也可以带入具体数字计算一下，确实不相等。 矩阵的运算顺序是从右往左，可能不太符合常规习惯。不过想一想前面提到的，矩阵运算其实就是对空间进行函数运算，再结合复合f(g(x))的写法：先计算g(x)，再计算f(g(x))，就不难理解了。

行列式

其实讲到的东西已经足以说明了矩阵的几何意义，后续提到的transform也只需要以上理解就可以了，不过我还是想继续抽一个其他概念简述一下，以说明矩阵的其他各种概念也都有着其相对应的实际(几何)意义。

如果大家还有印象，行列式的计算规则为 $det(\begin{bmatrix}a&b\\c&d\\\end{bmatrix})$= ad-bc，这一值代表着什么呢？我们一步步来看一下。

• 先假设c和b均为0，那这样矩阵对应的空间变换为：$\vec i$变为$a\vec i$，$\vec j$变为$d\vec j$，则此时$det(\begin{bmatrix}a&b\\c&d\\\end{bmatrix})$=$det(\begin{bmatrix}a&0\\0&d\\\end{bmatrix})$ =ad，看起来是表示空间上一个单位面积被缩放的倍数。

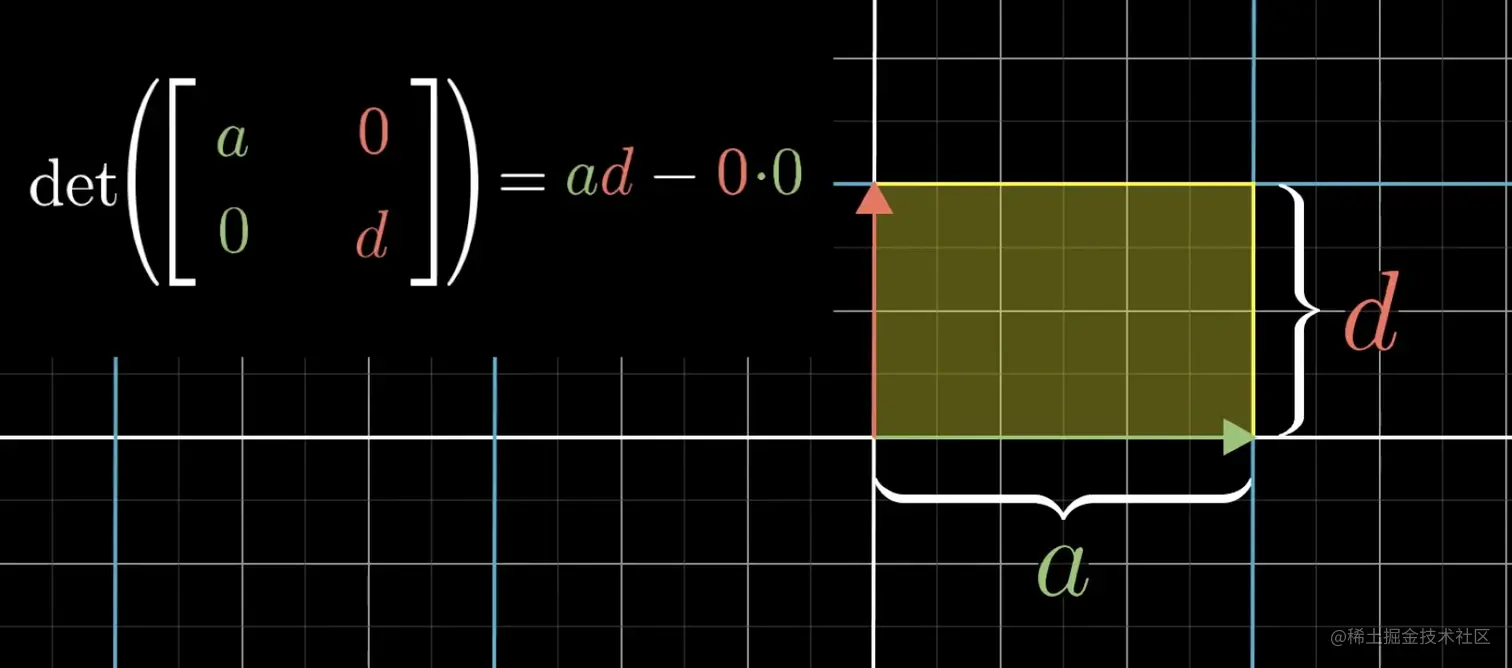
• 再恢复b不为0，这样$\vec i$变为$a\vec i$，$\vec j$变为$a\vec i+d\vec j$，从平面上来看变为了一个平行四边形，计算$det(\begin{bmatrix}a&b\\c&d\\\end{bmatrix})$=$det(\begin{bmatrix}a&b\\0&d\\\end{bmatrix})$ =ad，正好也等于平行四边形面积，依然是ad，

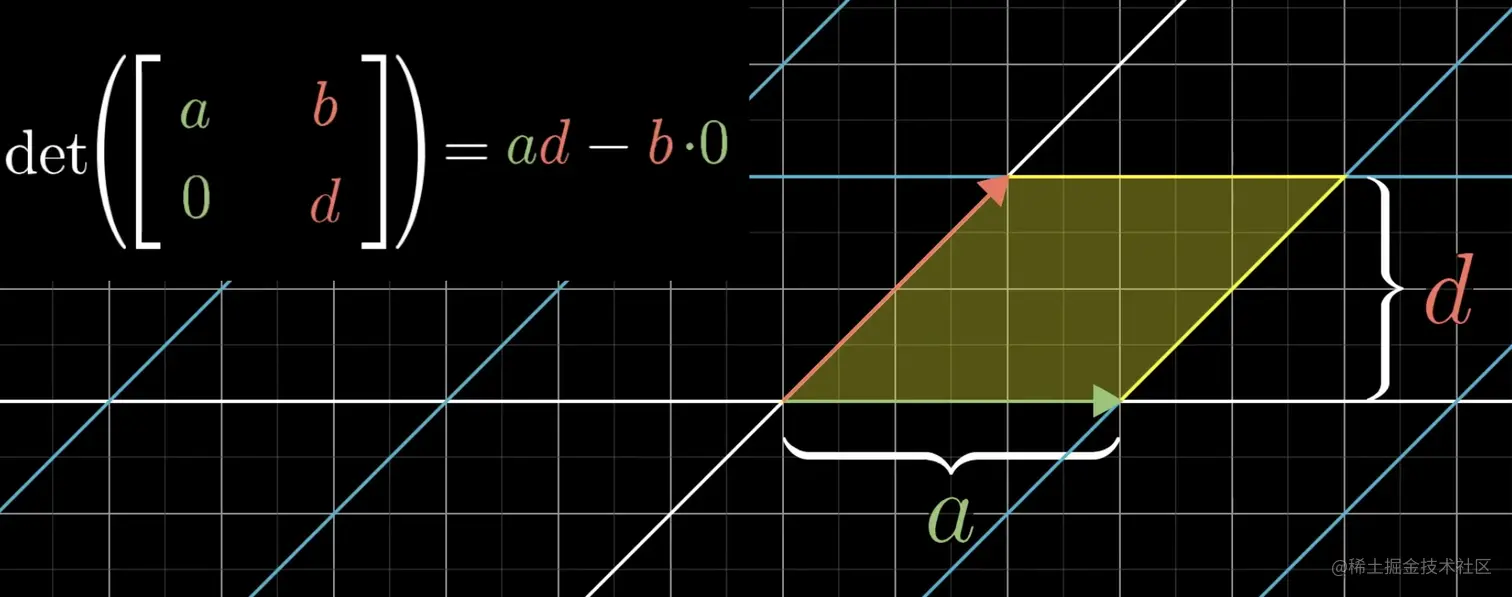
• 接着我们再恢复c部位0，此时$\vec i$变为$a\vec i+c\vec j$，$\vec j$变为$a\vec i+d\vec j$，变换如下图，停下来计算一下：$det(\begin{bmatrix}a&b\\c&d\\\end{bmatrix})$=(a+b)(c+d)-ac-bd-2bc=ad-bc，正好是基向量变换后围成的面积。

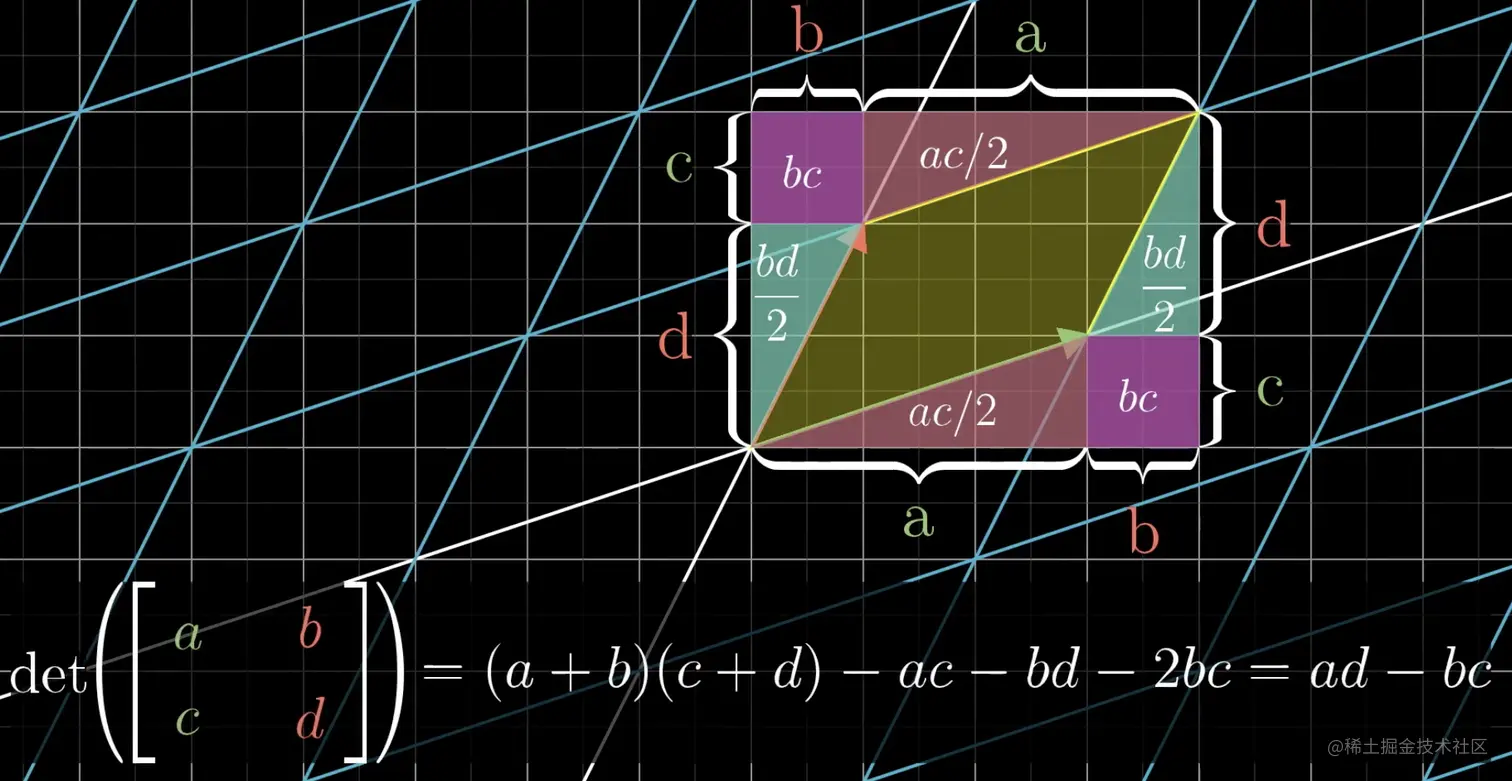所以，矩阵的行列式表示的是：经过矩阵变换后，平面单位面积的缩放倍数。

想一想对于公式det($\mathbf{M{_2}} \mathbf{M{_1}}$)=det($\mathbf{M{_2}}$)det($\mathbf{M{_1}}$)，你是否可以不用数学计算，只用一句话解释其中的道理呢？

假装过了一分钟。

我的理解：经过$\mathbf{M{_1}}$变换后，空间被缩放了det($\mathbf{M{_1}}$)倍，紧接着经过$\mathbf{M{_2}}$变换，（假设将此时的空间想成单位空间），那么变换后的空间不就是缩放了1* det($\mathbf{M{_1}}$)倍，而这里的1是原本其实是det($\mathbf{M{_1}}$)，也就是det($\mathbf{M{_2}} \mathbf{M{_1}}$)=det($\mathbf{M{_2}}$)det($\mathbf{M{_1}}$)，似乎也是显而易见，不需要任何证明。

还有很多其他矩阵的特性也都有其几何意义，比如逆矩阵、特征值等，这里就不一一说明了。

transform中的matrix

如果大家稍微有了解transform里有matrix这个用法，相信大部分人都不理解里面每个参数的意义，从而导致死记很难记住。当然这也并不影响我们日常开发，因为我们几乎用不到。不过理解了以上矩阵的变换，会发现根本不需要记，每个参数都很好理解，而一些我们常用的属性：rotate、translate其实都是一次矩阵变换，都是对matrix的封装。

验证demo，点击正在动画中的元素，console中会发现其transfrom为matrix。

基本格式

transform: matrix(a,b,c,d,e,f)

其对应的矩阵为A = $\begin{bmatrix}a&c&e\\b&d&f\\ 0&0&1\\\end{bmatrix}$，假设平面上的一点为(x,y)，则经过变换后为$\begin{bmatrix}a&c&e\\b&d&f\\ 0&0&1\\\end{bmatrix}\begin{bmatrix}x\\y\\ 1\\\end{bmatrix}$=$\begin{bmatrix}ax+cy+e\\bx+dy+f\\ 1\\\end{bmatrix}$。

再次回顾下，这里A为对平面（坐标系）的变换，其中(a,b)是变换后的基向量$\vec i$，(c,d)是变换后的基向量$\vec j$。基于上面的理解，我们知道一个平面的变换，用22的矩阵就可以，也就是$\begin{bmatrix}a&c\\b&d\\\end{bmatrix}$，为啥会多出e和f形成了33的矩阵，这个和translate有关，因此我们先来看下translate。

以下场景的demo

translate

translate属性表示为元素的位移，也就是不涉及到对坐标系的变换，因此改变参数中的a、b、c、d是没法做到的，我们需要增加一个单纯的位移维度，也就是对(x,y)平移(e,f)后坐标要变为(x+e,y+f)，且同时我们要保持$\begin{bmatrix}a&c\\b&d\\\end{bmatrix}$的功能不变（假设我们已经知道其作用，后面再讲）。

因此保持$\vec i$和$\vec j$不变，我们可以得到$\begin{bmatrix}1&0&e\\0&1&f\\ 0&0&1\\\end{bmatrix}\begin{bmatrix}x\\y\\ 1\\\end{bmatrix}$=$\begin{bmatrix}x+e\\y+f\\ 1\\\end{bmatrix}$，也就得到了变换后的点(x+e,y+f)。加上对平面的变换后，我们就可以得到以上的通用变换矩阵$\begin{bmatrix}a&c&e\\b&d&f\\ 0&0&1\\\end{bmatrix}$了。

小结：translate仅需用到参数e和f，translate(e,f)对应matrix(1，0，0，1，e，f)。

scale

scale属性表示对元素的缩放，也就是坐标系缩放了，但是不会变形；即只进行矩阵的数乘变换，$\vec i$变为$m\vec i$，$\vec j$变为$n\vec j$，其中m和n为标量。

对应到矩阵上，即$\begin{bmatrix}1&0\\0&1\\\end{bmatrix}$变换为$\begin{bmatrix}m&0\\0&n\\\end{bmatrix}$，也就是$\begin{bmatrix}a&0\\0&d\\\end{bmatrix}$。

小结：scale仅需用到参数a和d，scale(a, b)对应matrix(a，0，0，d，0，0)。

rotate

rotate属性表示对元素的旋转，这里就涉及到三角函数。旋转$\theta$后，$\vec i$变为$(\cos\theta ,\sin\theta)$，$\vec j$变为$(-\sin\theta，\cos\theta )$。

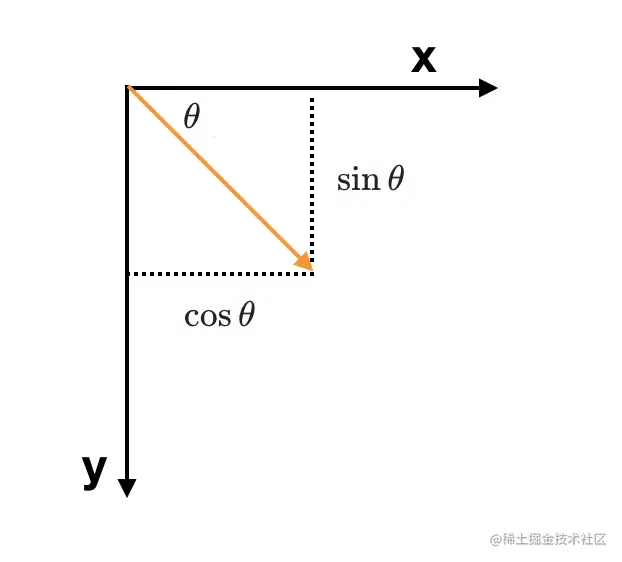对应到矩阵上，即$\begin{bmatrix}1&0\\0&1\\\end{bmatrix}$变换为$\begin{bmatrix}\cos\theta&-\sin\theta \\\sin\theta &\cos\theta \\\end{bmatrix}$。 小结：rotate需用到参数a、b、c和d，rotate($\theta$)对应matrix($\cos\theta$，$\sin\theta$，$-\sin\theta$，$\cos\theta$，0，0)。

组合使用

transform的其他属性就不一一说明了，我们来看看这些属性如何组合使用。

先问个问题：如果我们想要将元素缩小为0.5倍，且右移50px，会怎么写？

.element{ 
    transform: translate(50px, 0) scale(0.5); 
} 

.element{ 
    transform: scale(0.5) translate(50px, 0); 
} 

以上2种写法有区别吗？

上面我们提到，每次矩阵左乘是一次变换，多次变换就多次左乘即可。假设Translate的矩阵为$\mathbf{T}$，Scale的矩阵为$\mathbf{S}$，元素上的点矩阵为$\mathbf{E}$。

• $\mathbf{STE}$：先$\mathbf{T}$，后$\mathbf{S}$，对应写法transform: translate(50px, 0) scale(0.5); ，表示对元素先Translate，后Scale。
• $\mathbf{TSE}$：先$\mathbf{S}$，后$\mathbf{T}$，对应写法transform: scale(0.5) translate(50px, 0);， 表示对元素先Scale，后Translate。

我们已经知道矩阵乘法不满足交换律，也就是$\mathbf{ST}$与$\mathbf{TS}$不相等，那说明transform: translate(50px, 0) scale(0.5); 和transform: scale(0.5) translate(50px, 0);是不一样的。那我们来看看实际是不是这样？

通过demo可以发现，两者并不一样：

• 先使用scale缩小到0.5倍之后，后续的translate的50px也缩小为了0.5倍，即50*0.5=25px；
• 先使用translate，对于平面没有影响，因此对后续的scale没有影响

因此，我们只要时刻记住，transform变换是针对当前元素所在的整个平面的变换而不是仅针对当前元素，我们就能正确的组合使用了。

另外，知道了组合使用实际上只是矩阵相乘，我们也可以连续使用相同的属性（不一定需要使用calc），比如：

• transform: translate(100%, 0) translate(50px, 0);，先右移100%，再右移50px
• transform: scale(2) scale(3);先放大2倍，再基于此放大3倍，共2*3=6倍，而不是2+3=5倍。

思考：非方阵

上面提到的m * n矩阵都是方阵，即行数m和列数n相等的矩阵。那非方阵代表着什么呢？ 比如：

• m < n， $\begin{bmatrix}a&c&e\\b&d&f\\\end{bmatrix}$ 3*3代表什么？
• m > n， $\begin{bmatrix}a&d\\b&e\\ c&f\\\end{bmatrix}$ 2*2代表什么？

这里就不提供答案了，如果理解了上面的内容，相信很容易想清楚~

本文只提到了矩阵的一些基本性质，但其实这些基础性质就足以说明了其几何意义，如果大家以后看到矩阵能想到去想一想它的几何意义，那本次分享的目的就达到啦！

ps：看过视频之后，我去网上查过一些关于这方面的文章，由于这本身是个用文字很难说清楚且很容易劝退的主题，所以大多数文章都很难让人看下去，本文也可能是这样。所以我越发开心看到这个视频合集，虽然以后也许不一定能用上，但它也带来了那些看视频的愉快时光，以及写本文时的“才思泉涌”和热情高涨🐶！ ​

❤️ 谢谢支持

以上便是本次分享的全部内容，希望对你有所帮助^_^

喜欢的话别忘了 分享、点赞、收藏 三连哦~。

欢迎关注公众号 ELab团队 收货大厂一手好文章~

我们来自字节跳动，是旗下大力教育前端部门，负责字节跳动教育全线产品前端开发工作。

我们围绕产品品质提升、开发效率、创意与前沿技术等方向沉淀与传播专业知识及案例，为业界贡献经验价值。包括但不限于性能监控、组件库、多端技术、Serverless、可视化搭建、音视频、人工智能、产品设计与营销等内容。

欢迎感兴趣的同学在评论区或使用内推码内推到作者部门拍砖哦 🤪

字节跳动校/社招内推码: W6WGRQM

投递链接: jobs.toutiao.com/s/dPNW5wp