搞定softmax和交叉熵

菜狗闻星学AI
1,206 阅读1分钟

搞定softmax和交叉熵

1. 信息量的度量-熵

信息量

信息的多少与接收者说到的信息时感到的惊讶程度相关，信息所表达的事件越不可能发生，越不可预测，信息量就越大

I=log⁡a1P(x)I=\log _a\frac{1}{P\left( x \right)}

信息量的单位和上式中的a有关

  • a=2,则信息量的单位为比特（bit）------最为常用
  • a=e,则信息量的单位为奈特(nat)
  • a=10,则信息量的单位为特莱(Hartley)

平均信息量

我们称平均信息量为熵，举个例子

H(X)=−Σ(pi)log⁡p(xi)H\left( X \right) =-\Sigma \left( p_i \right) \log p\left( x_i \right)

一离散信源有0,1,2,3这4个符号组成概率分别如下

0123
0.3750.250.250.125
H(X)=−p0log⁡2P(x0)−p1log⁡2P(x1)−p2log⁡2P(x2)−p3log⁡2P(x3)H\left( X \right) =-p_0\log _2P\left( x_0 \right) -p_1\log _2P\left( x_1 \right) -p_2\log _2P\left( x_2 \right) -p_3\log _2P\left( x_3 \right)
H(X)=−0.375log⁡20.375−0.25log⁡20.25−0.25log⁡20.25−0.125log⁡20.125=1.90564H\left( X \right) =-0.375\log _20.375-0.25\log _20.25-0.25\log _20.25-0.125\log _20.125=1.90564

2. 交叉熵

以手写体数字识别为例为来生动的演示交叉熵

H(p,q)=Σxp(x)log⁡(1q(x))H\left( p,q \right) =\underset{x}{\Sigma}p\left( x \right) \log \left( \frac{1}{q\left( x \right)} \right)
(image0)  label  =  [1000]  predicate=[0.80.10.10](image2)  label  =  [0001]  predicate=[0.70.10.10.1]\left( image0 \right) \,\, label\,\,=\,\,\left[ \begin{array}{c} 1\\ 0\\ 0\\ 0\\ \end{array} \right] \,\,predicate=\left[ \begin{array}{c} 0.8\\ 0.1\\ 0.1\\ 0\\ \end{array} \right] \\ \left( image2 \right) \,\, label\,\,=\,\,\left[ \begin{array}{c} 0\\ 0\\ 0\\ 1\\ \end{array} \right] \,\,predicate=\left[ \begin{array}{c} 0.7\\ 0.1\\ 0.1\\ 0.1\\ \end{array} \right]
H(p,q)=−1log⁡20.8−1log⁡10.1H\left( p,q \right) =-1\log _20.8-1\log _10.1

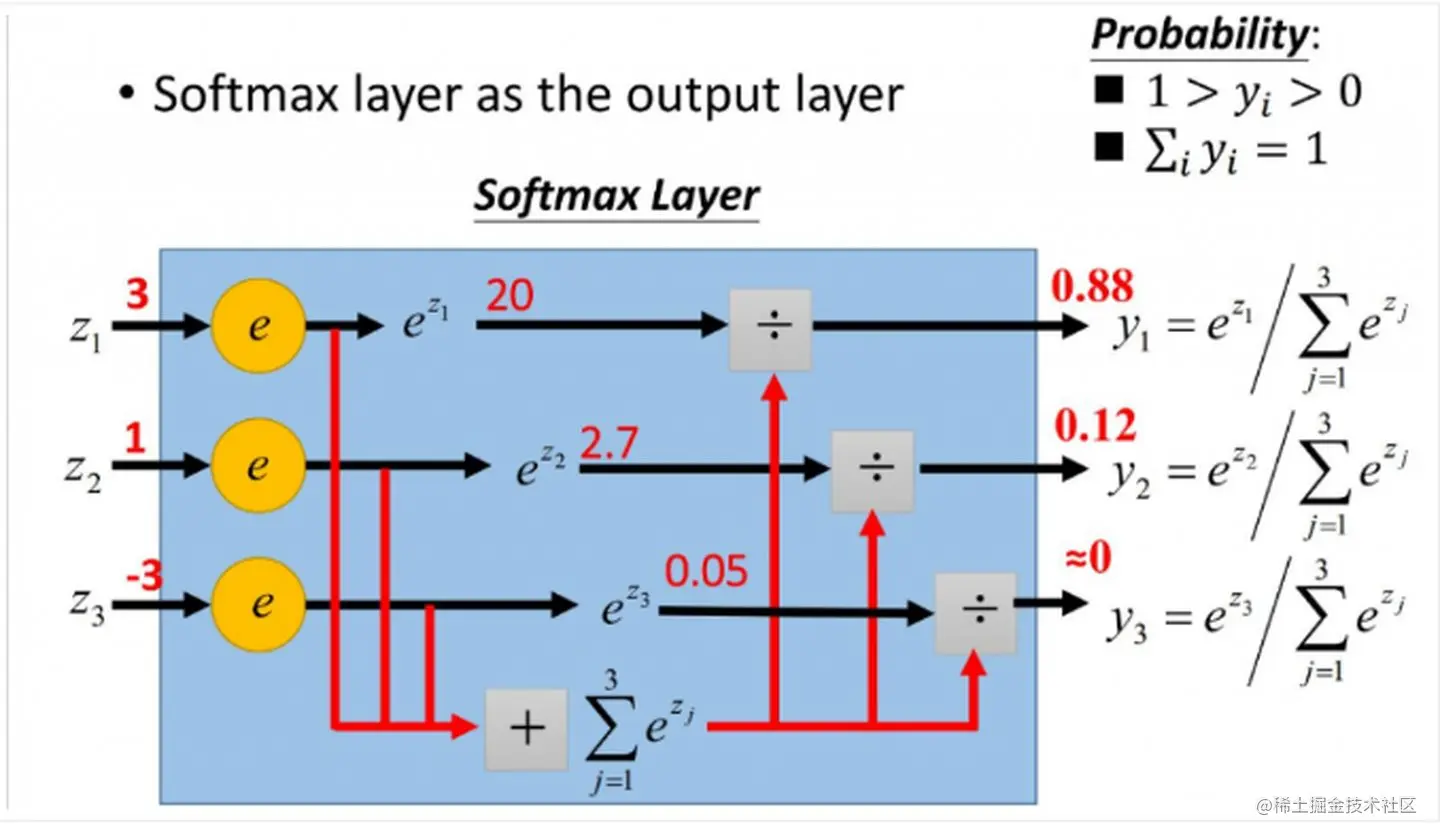
3. softmax

Yi=eziΣi=1neziY_i=\frac{e^{z_i}}{\Sigma _{i=1}^{n}e^{z_i}}
请看以下例子，输入为Z,输出为Y,且Y各个概率之和为1\text{请看以下例子，输入为Z},\text{输出为Y},\text{且Y各个概率之和为}1
z=[z1z2z3]=[31−3]z=\left[ \begin{array}{c} \mathrm{z}_1\\ \mathrm{z}_2\\ \mathrm{z}_3\\ \end{array} \right] =\left[ \begin{array}{c} 3\\ 1\\ -3\\ \end{array} \right]
∑i=13ezi=e3+e1+e−3=22.8536\sum_{i=1}^3{e^{z_{\mathrm{i}}}}=\mathrm{e}^3+\mathrm{e}^1+\mathrm{e}^{-3}=22.8536
第一步实现所有数映射为非负数z′=[e3e1e−3]\text{第一步实现所有数映射为非负数}z'=\left[ \begin{array}{c} e^3\\ e^1\\ e^{-3}\\ \end{array} \right]
∑i=13ezi=e3+e1+e−3=22.8536\sum_{i=1}^3{e^{z_{\mathrm{i}}}}=\mathrm{e}^3+\mathrm{e}^1+\mathrm{e}^{-3}=22.8536
第二步实现所有数映射到0-1范围之内且和为1 Y=z′∑i=13ezi=[e3e1e−3]∑i=13ezi=[e3e1e−3]22.8536=[20.08552.718280.0497871]22.8536≈[0.880.120]\text{第二步实现所有数映射到0-1范围之内且和为1 } \mathrm{Y}=\frac{z'}{\sum_{i=1}^3{e^{z_{\mathrm{i}}}}}=\frac{\left[ \begin{array}{c} e^3\\ e^1\\ e^{-3}\\ \end{array} \right]}{\sum_{i=1}^3{e^{z_{\mathrm{i}}}}}=\frac{\left[ \begin{array}{c} e^3\\ e^1\\ e^{-3}\\ \end{array} \right]}{22.8536}=\frac{\left[ \begin{array}{c} 20.0855\\ 2.71828\\ 0.0497871\\ \end{array} \right]}{22.8536}\approx \left[ \begin{array}{c} 0.88\\ 0.12\\ 0\\ \end{array} \right]

img

softmax输出作为交叉熵的输入

联合本文的第2部分和第3部分，softmax层的输出概率向量可以作为交叉熵损失函数的输入，用在分类问题上。

Y=z′∑i=13ezi=[e3e1e−3]∑i=13ezi=[e3e1e−3]22.8536=[20.08552.718280.0497871]22.8536≈[0.880.120]\mathrm{Y}=\frac{z'}{\sum_{i=1}^3{e^{z_{\mathrm{i}}}}}=\frac{\left[ \begin{array}{c} e^3\\ e^1\\ e^{-3}\\ \end{array} \right]}{\sum_{i=1}^3{e^{z_{\mathrm{i}}}}}=\frac{\left[ \begin{array}{c} e^3\\ e^1\\ e^{-3}\\ \end{array} \right]}{22.8536}=\frac{\left[ \begin{array}{c} 20.0855\\ 2.71828\\ 0.0497871\\ \end{array} \right]}{22.8536}\approx \left[ \begin{array}{c} 0.88\\ 0.12\\ 0\\ \end{array} \right]
label=  [100]\mathrm{label} =\,\,\left[ \begin{array}{c} 1\\ 0\\ 0\\ \end{array} \right]
H(x)=−log⁡2(0.88)=0.184425\mathrm{H}\left( \mathrm{x} \right) =-\log _2\left( 0.88 \right) =0.184425
avatar
文章
阅读
粉丝