【学习笔记】相似性度量使用的一些距离（一）

欧氏距离 Euclidean Distance

比较常用的距离，常用于表示空间中两个点或多点间的直线距离，对于n维空间，存在点x和y（用n维向量表示），有：

然而欧式距离的局限性很大，包括：

1. 会受到量纲（单位标准，scale）的影响 例如，提取一个人身高和体重的特征，身高用cm为单位，体重用g为单位，A身高160体重60000，B身高160体重59000，C身高170体重60000，度量他们的欧式距离：

显然，$d(A,B)>d(A,C)$，然而根据常识可以判断A和B的体型比B和C更近，可以发现，欧式距离在这个案例中不适用。

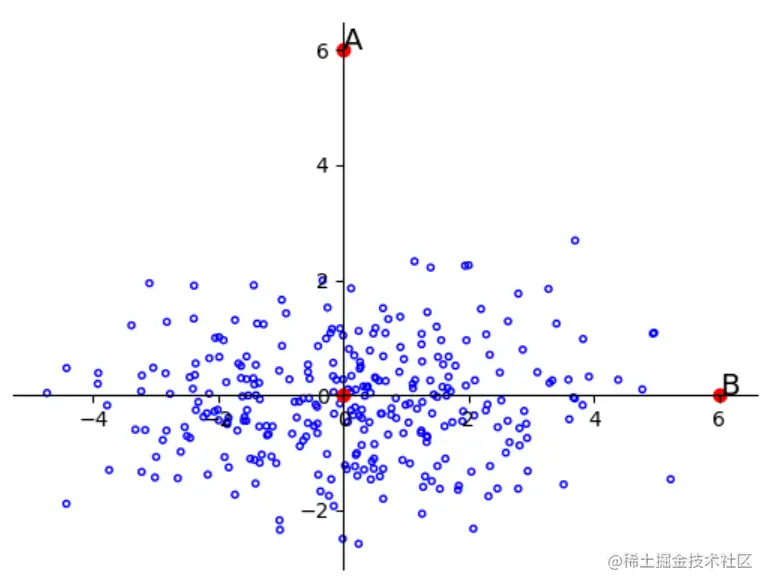
2. 会受到样本分布的影响 如下图所示，如果用欧氏距离度量AB两点到样本集合中心点的距离，那会得到AB两点距离相同的结论，然而根据分布看显然B点比A点更可能属于这个样本集。

马氏距离 Mahalanobis Distance

鉴于上述欧式距离的局限性，马氏距离被提出了修正这些问题。要学习马氏距离需要了解方差、协方差和协方差矩阵的一些基本知识，这些在主成因分析PCA中有提到过。马氏距离的物理意义是在规范化主成因空间（即通过对数据使用PCA方法，形成新的坐标轴）中的欧式距离。如下图所示：

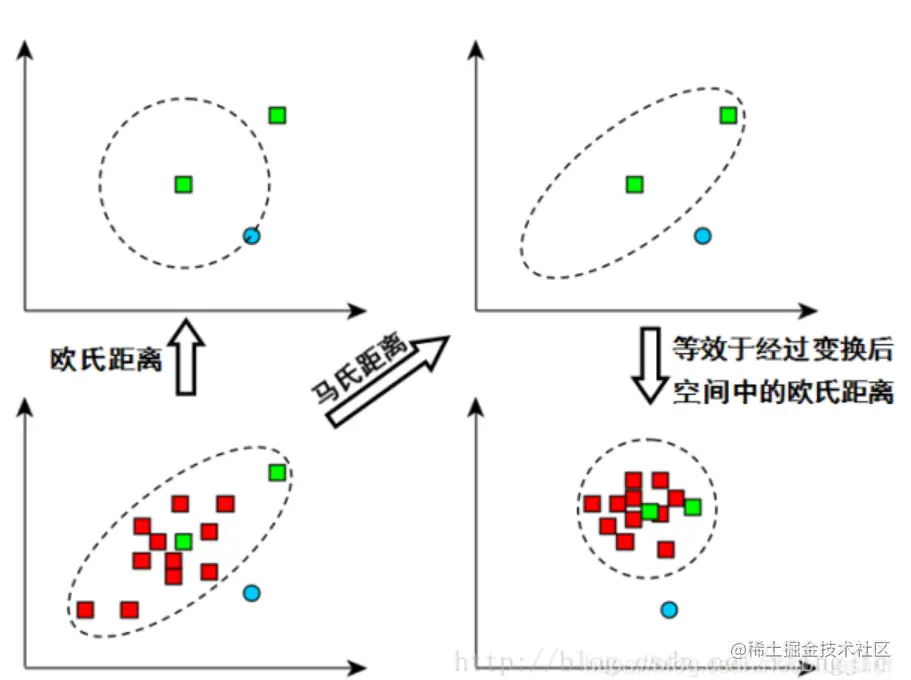
马氏距离总共分为两个步骤：

• 首先旋转坐标轴使各个维度间线性无关。
• 然后将不同维度上的数据压缩成为方差为1的数据集（归一化）。

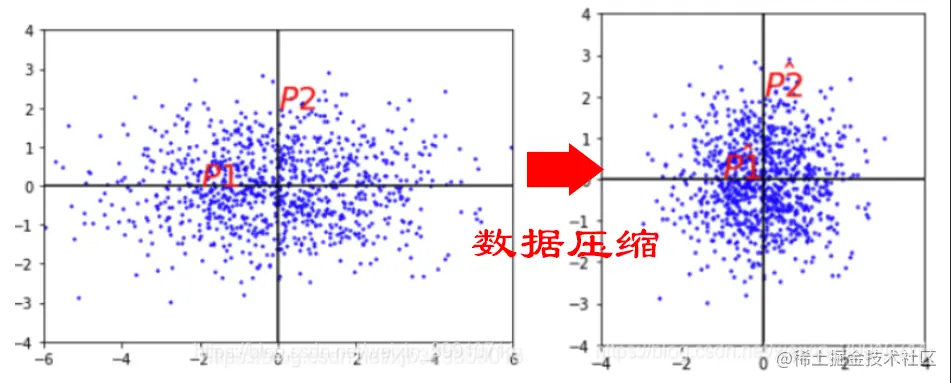
为什么要压缩数据（归一化） 在下图所示的空间中，P1、P2点到数据集中心的欧式距离是一样的，但显然P1比P2更可能属于该数据集，通过归一化方法，使数据在不同维度上方差统一，同时消除量纲的影响。

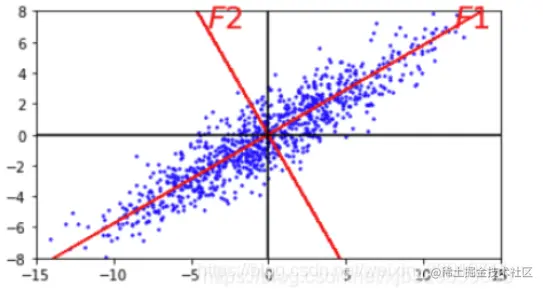
为什么要旋转坐标轴 如下图所示，当不同维度间具有相关性（即联合分布和坐标轴有一定角度）时，数据只沿着横纵坐标轴的方向压缩，并不能改变图中A和B两点到中心的马氏距离计算结果。

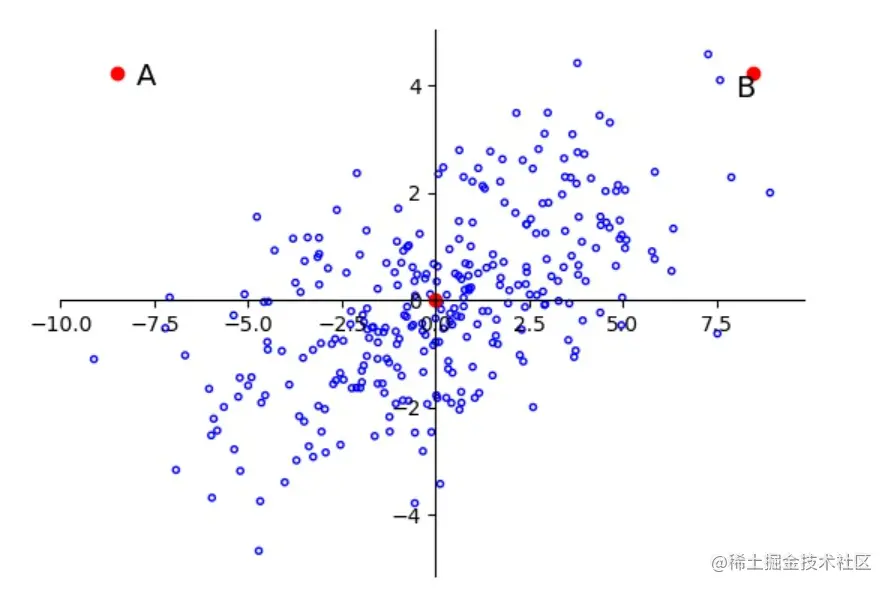
更最好的压缩方法是沿着F1和F2的方向压缩，因此需要将坐标轴旋转成F1和F2的方向，此时就需要通过协方差矩阵确定如何旋转。

理解是旋转坐标轴，在操作中是旋转改变数据点，假设原始数据集为$X(n\times m)$，n为样本总数，m为样本特征维度：

通过旋转矩阵$U$旋转到新的坐标系统（即上文说的F1和F2）中得到一个新的数据集$F$。

新样本集的均值为$\mu_F=(\mu_{F1},...\mu_{Fm})^T$，可得：

由于将数据集旋转后不同维度间是线性无关的，所以新数据集$F$的协方差矩阵$\Sigma_{F}$应为对角阵，且主对角元素（特征值）均为每个维度的方差：

由协方差矩阵的公式和前面的推倒可得：

对于数据集$X$，其中一样本点$x$到样本中心$\mu_X$的马氏距离等同于求点$F_x$到样本中心$\mu_F$的欧氏距离：

有上述内容可得马氏距离的定义：

对于一个均值为$\mu=(\mu_1,...,\mu_n)^T$且协方差矩阵为$\Sigma$的多变量空间$x=(x_1,...,x_n)^T$，其马氏距离为：

或可以定义为两个服从同一分布且协方差矩阵为$\Sigma$的随机变量$\vec{x}$和$\vec{y}$间的差异程度：

当协方差矩阵为单位矩阵（即$\vec{x}$和$\vec{y}$的联合分布为正圆，$\vec{x}$和$\vec{y}$独立同分布线性无关）时，上式化为欧式距离的算法：

曼哈顿距离 Manhattan Distance

跟直线距离计算不同，曼哈顿距离常用于计算路径，指空间中两点或多点间连线对应坐标轴投影的距离和，如下图所示。

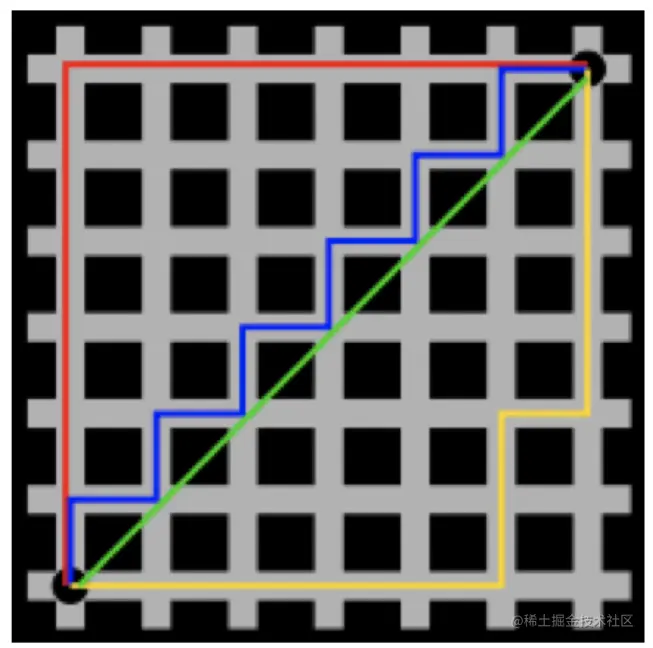
对于二维平面的点$a(x_1,y_1)$和$b(x_2,y_2)$间的曼哈顿距离定义为：

扩展到n维空间（$a(x_{11},...,x_{1n})$和$b(x_{21},...,x_{2n})$）得到：