梯度下降

Ann_
228 阅读5分钟

这是我参与8月更文挑战的第12天，活动详情查看：8月更文挑战

前边的代价函数就是使用梯度下降而得到其最小值的。梯度下降当然也可以用于其他的代价函数J。

image.png

梯度下降是什么？

对于一个代价函数J(θ0,θ1,θ2,…)J(\theta_0,\theta_1,\theta_2,…)，我们想要使其最小化：

  • 初始时候令θi\theta_i都为0
  • 逐渐改变θi\theta_i的值
  • 直到得到最小值或者局部最小值

用图解释一下梯度下降，对于代价函数J(θ0,θ1)J(\theta_0,\theta_1)，如下一个三维图形，你先想象成这是一篇山区。你从任意一个点开始下山，每次环顾四周，找一个同样步长的最低点向下移一步，直到最低点。

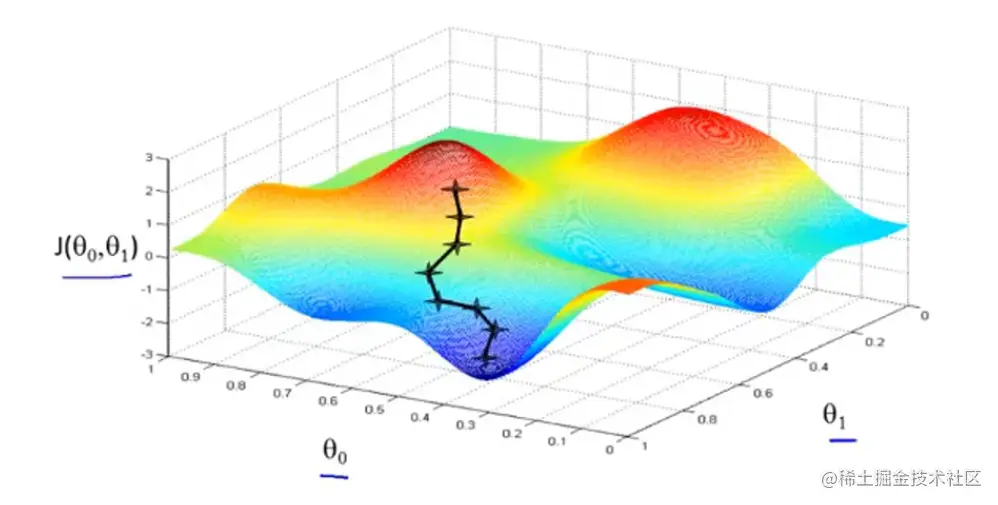
image.png

但是如果你起始点不同，可能会找到另一个最低点。也就是说梯度下降算法起始点不同找到的最优解可能是不同的。

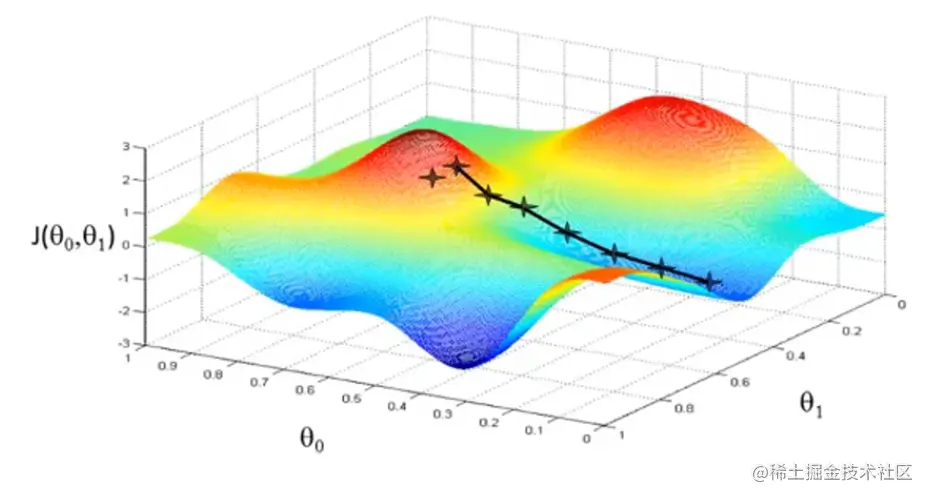
image.png

梯度下降算法定义：

image.png

  • :=:=是赋值符号，比如a:=ba:=b就是给a赋上b的值
  • ==是判断符号，比如a=ba=b如果两个值相等返回true，否则返回false
  • α\alpha控制梯度下降的步长，如果α\alpha较大那下降的就会很迅速
  • ∂∂θjJ(θ0,θ1)\frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)求导
  • 对于上述公式正确的执行步骤：
    • 使用θ0,θ1\theta_0,\theta_1更新temp
    • 使用temp更新θ0,θ1\theta_0,\theta_1

解释一下α∂∂θjJ(θ0,θ1)\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)有什么用

  • α\alpha前边说了，它的大小控制梯度下降的步长大小，可以称之为学习速率，其取值永远为正数。
  • 对于∂∂θjJ(θ0,θ1)\frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)求导公式我们依旧先从最简单的例子开始。

先解释导数部分

假设现在的代价函数是J(θ1)J(\theta_1)其中θ1∈R\theta_1 \in R，那他的图像应该是个一元二次函数。

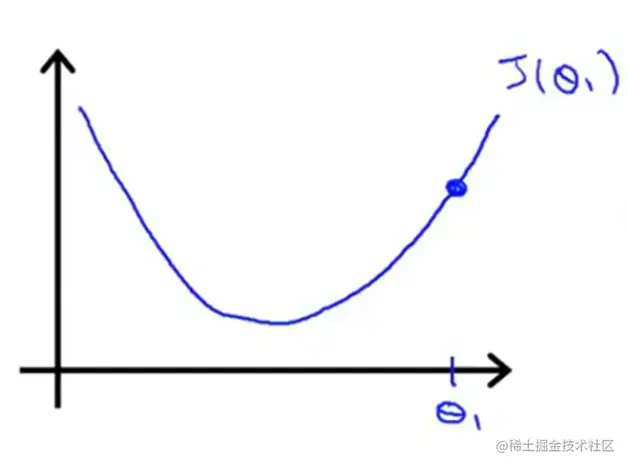
image.png

现在从右边蓝色这个点进行梯度下降，那就会得到结果θ1:=θ1−αddθ1J(θ1)\theta_{1}:=\theta_{1}-\alpha \frac{d}{d \theta_{1}} J\left(\theta_{1}\right)

你可能会注意到原来公式中的∂变为d了，

符号 d 与符号 ∂ 的区别是什么？

∂\partial 指偏微分。对于一个多元函数 f(x,y),∂f∂xf(x, y), \frac{\partial f}{\partial x} 相当于固定 yy 变量, 对 xx 进行求导。

d\mathrm{d} 指全微分。对于一个多元函数 f(x,y),df=∂f∂x dx+∂f∂y dyf(x, y), \mathrm{d} f=\frac{\partial f}{\partial x} \mathrm{~d} x+\frac{\partial f}{\partial y} \mathrm{~d} y 。

在复合函数中, 全微分的概念更加有用。设多元函数 f(x(t),y(t))f(x(t), y(t)), 则 df dt=∂f∂xdx dt+∂f∂ydy dt\frac{\mathrm{d} f}{\mathrm{~d} t}=\frac{\partial f}{\partial x} \frac{\mathrm{d} x}{\mathrm{~d} t}+\frac{\partial f}{\partial y} \frac{\mathrm{d} y}{\mathrm{~d} t} 。

对于单变量函数, 偏微分和全微分没有区别, 所以均用 ddx\frac{\mathrm{d}}{\mathrm{d} x} 表示。

我们都知道在上图中导数的几何意义是过蓝色点切线的斜率，而图中可知这个斜率一定是个正数。再加上前边的条件α\alpha学习速率一定是正数，那原式就可以理解为θ1:=θ1−一个正数\theta_{1}:=\theta_{1}-一个正数，那θ1\theta_{1}一定会向左移，从而使J(θ1)J(\theta_{1})减小。

为什么我把“从而使J(θ1)J(\theta_{1})减小”这句话划掉了呢，因为你考虑一下，如果α取值过大，那它可能移动的太大而越过了最小值，而在最小值左右两侧反复横跳。

同理看下图，如果初始θ1\theta_{1}在最低点的左侧，那现在改点的斜率是个负数，此时原式就可以理解为θ1:=θ1−一个负数\theta_{1}:=\theta_{1}-一个负数，导致θ1\theta_{1}增大，使其右移。

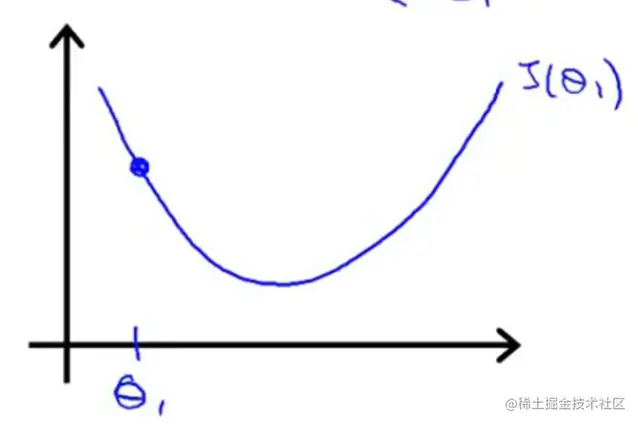
image.png

再解释一下α

现在再讨论一下α。如果过大或者过小会有什么影响。

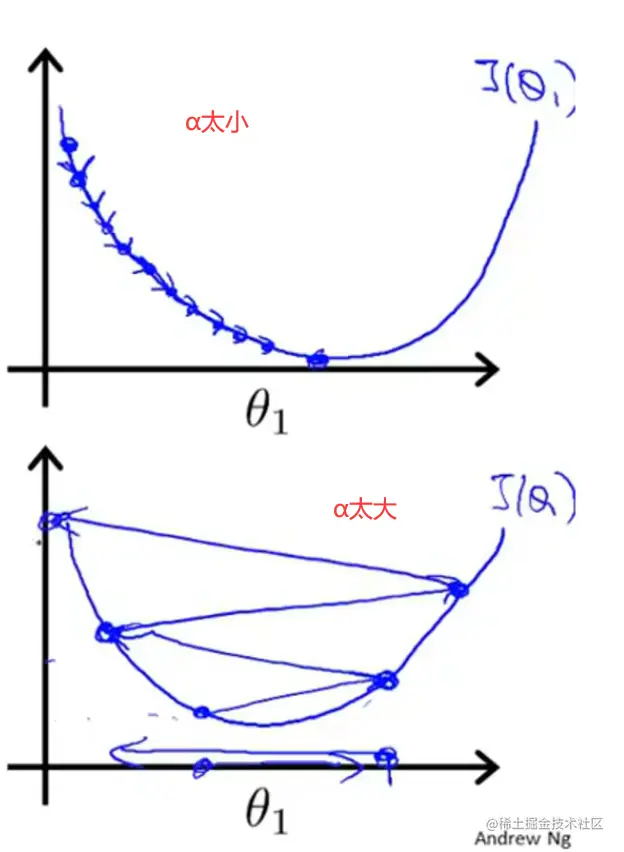
If α is too small, gradient descent can be slow. If a is too large, gradient descent can overshoot the minimum It may fail to converge or even diverge.

如果α太小，那梯度下降的速度就会很慢；如果太大，就会出现我上边提到的状况，可能直接越过最小值，在最小值左右两边反复横跳，离得原来越远（为什么会离得越来越远慢慢往下看就懂了）。

image.png

提问！

如果此时θ1\theta_{1}已经处于一个局部最优点，那会如何移动？

（？我也不知道为啥吴恩达老师会提这种问题，学过高中数学的就会回答这个问题了吧66DABEE6.png）

最低点切线是水平的，斜率为0，所以公式就是θ1:=θ1−α×0=θ1\theta_{1}:=\theta_{1}-\alpha \times 0 = \theta_1 ，到达局部最优解之后就停在原地不动了。

Gradient descent can converge to a local minimum even with the learning rate α fixed.

（α取值合适的前提下）虽然α是固定值，但是梯度下降却可以取得局部最小值。

As we approach a local minimum, gradient descent will automatically take smaller steps. So, no need to decrease α over time.

因为梯度下降越接近局部最小值，下降步长会越小，也就是说下降步长会随着逐渐靠近局部最优解而逐渐减小，因此我们无需改变α的值就可以顺利取到局部最小值。

看下图理解一下：

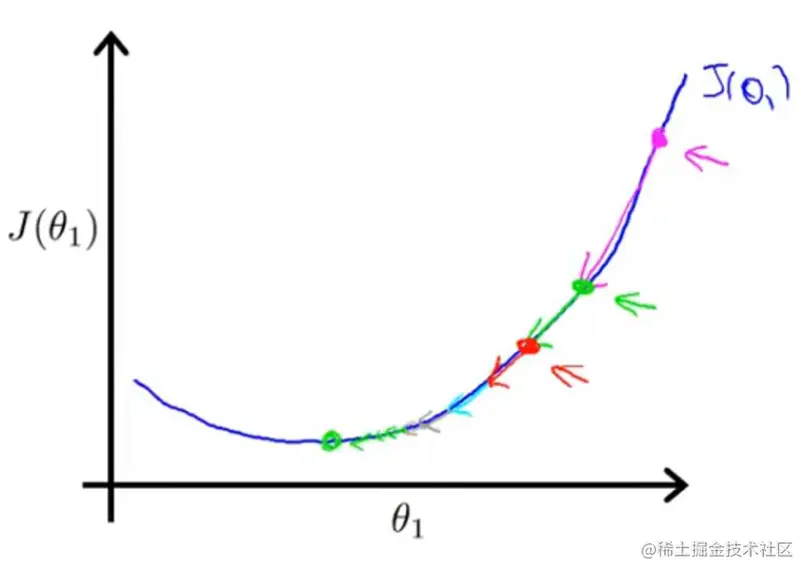
image.png

从最右侧粉色的点开始进行梯度下降，下降以后到达绿色的点。 θ1:=θ1−α×kpink\theta_{1}:=\theta_{1}-\alpha \times k_{pink}

从绿色点进行梯度下降，θ1:=θ1−α×kgreen\theta_{1}:=\theta_{1}-\alpha \times k_{green}

红色的点进行梯度下降：θ1:=θ1−α×kred\theta_{1}:=\theta_{1}-\alpha \times k_{red}

这三个点有什么区别？

越接近最低点，曲线越平缓，下降点的斜率越小。

对于θ1:=θ1−αddθ1J(θ1)\theta_{1}:=\theta_{1}-\alpha \frac{d}{d \theta_{1}} J\left(\theta_{1}\right)，其中ddθ1J(θ1)\frac{d}{d \theta_{1}} J\left(\theta_{1}\right)逐渐减小，会导致αddθ1J(θ1)\alpha \frac{d}{d \theta_{1}} J\left(\theta_{1}\right)逐渐减小，也就是每次θ1\theta_{1}减的值逐渐减小，使θ1\theta_{1}移动逐渐减缓。

回到线性回归

既然我们已经弄懂了代价函数J(θ1)J(\theta_1)，那现在就回到J(θ0,θ1)J(\theta_0,\theta_1)。

∵J(θ0,θ1)=12m∑i=1m(hθ(x(1))−y(i))2\because J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(1)}\right)-y^{(i)}\right)^{2}

∴∂∂θjJ(θ0,θ1)=∂2θj⋅12m∑i=1m(hθ(x(i))−y(i))2\therefore \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)=\frac{\partial}{2 \theta_{j}} \cdot \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}

∵hθ(x)=θ0+θ1x\because h_{\theta}(x)=\theta_{0}+\theta_{1} x

∴∂∂θjJ(θ0,θ1)=∂2θj⋅12m∑i=1m(hθ(x(i))−y(i))2=∂∂θj12m∑i=1m(θ0+θ1x(i)−y(i))2\therefore \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)=\frac{\partial}{2 \theta_{j}} \cdot \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}=\frac{\partial}{\partial \theta_{j}} \frac{1}{2 m} \sum_{i=1}^{m}\left(\theta_{0}+\theta_{1} x^{(i)}-y^{(i)}\right)^{2}

所以此时：(这个感兴趣的自己求嗷……我直接写现成结果了。)

θ0:∂∂θ0J(θ0,θ1)=1m∑i=1m(hθ(x(i))−y(i))θ1:∂∂θ1J(θ0,θ1)=1m∑i=1m(hθ(x(i))−y(i))⋅x(i)\begin{aligned} &\theta_{0}: \frac{\partial}{\partial \theta_{0}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \\ &\theta_{1}: \frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x^{(i)} \end{aligned}

推导过程写完了，得出结论，对于线性回归来说，梯度下降如下：

image.png

还记得解释什么叫梯度下降时候使用的三维图吗（就是那个想象成下山那个图，不记得的往上翻一下。） 线性回归的代价函数一般不会那么复杂，always going to be a bow-shaped function. 碗状图。专业术语叫“convex function”。

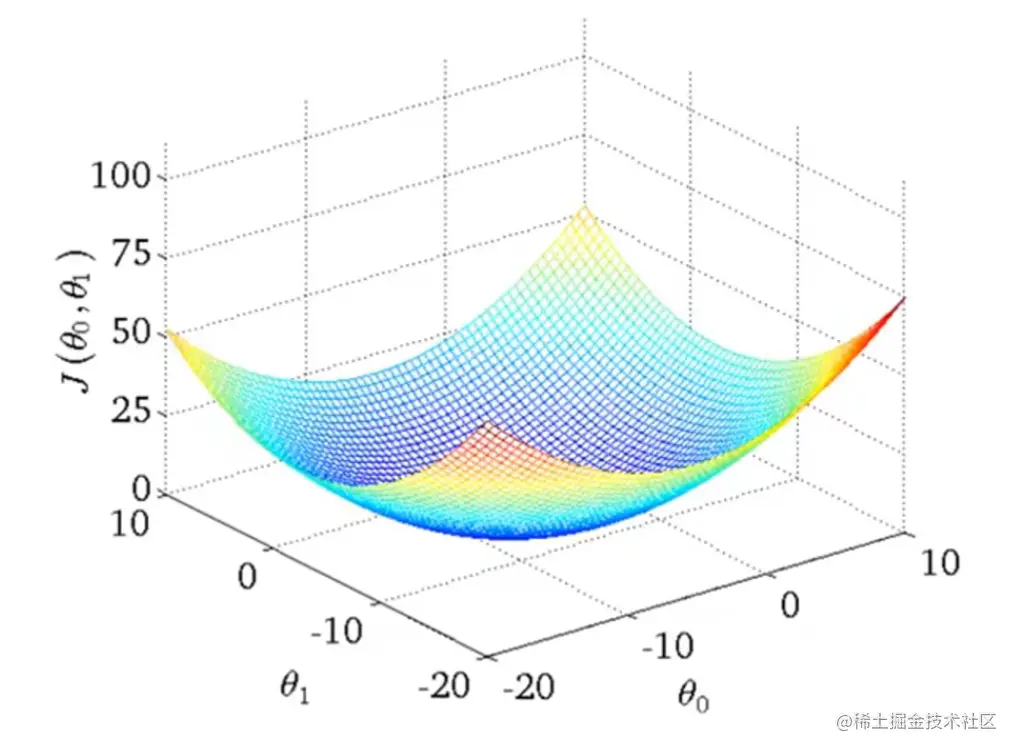
image.png

这种图不仅看起来比那种图简单，实际操作也简单，没有局部最优解，只有全局最优解，也就是说不管你从哪里开始最后找到的最优解都是一样的。

再回到之前的例子，还是这个等高图，从点1开始进行梯度下降，最后找到最优解（此时已经找到代价函数的最小值）。每一步都对应一个回归函数图像，点1-4和最优解的回归函数都画出来了，肉眼可见的最后一张图拟合程度最高。

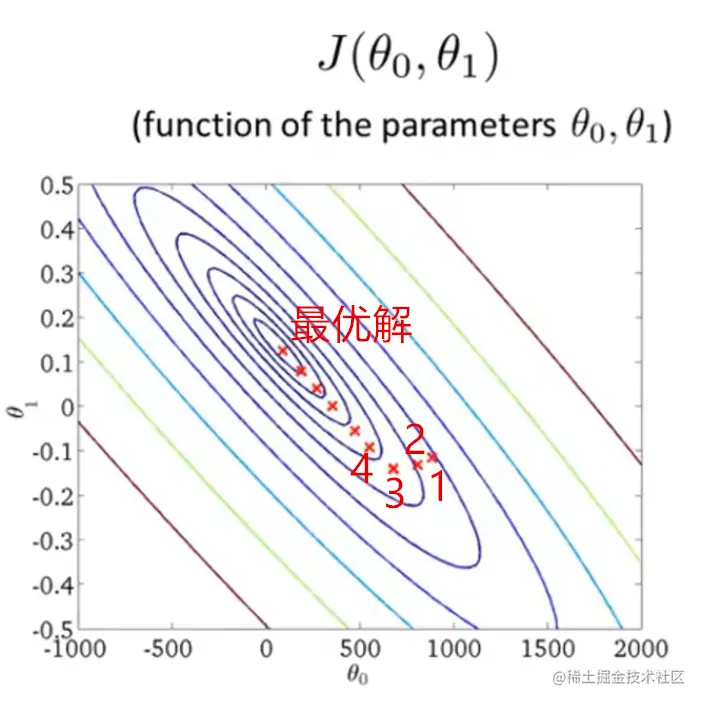
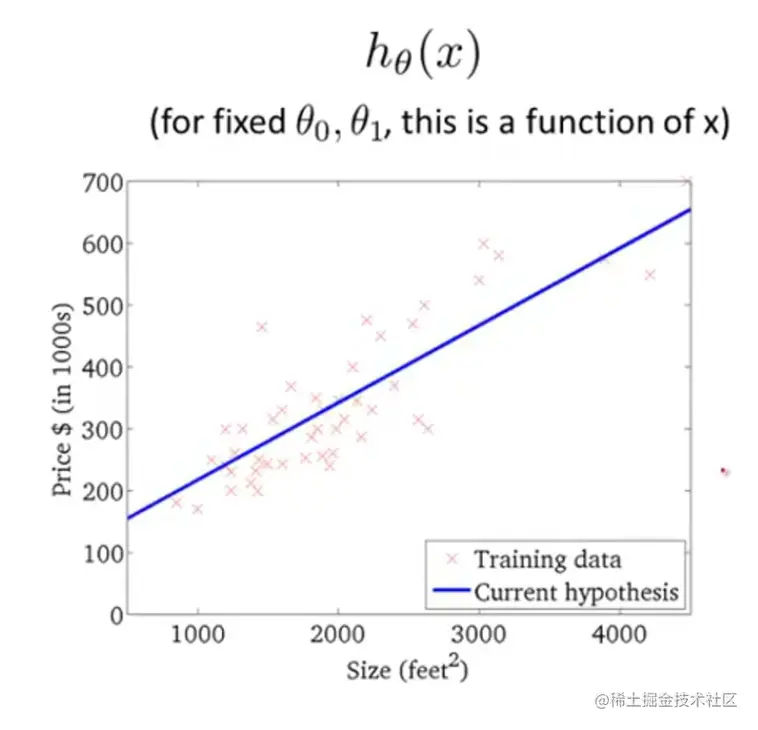
放一个详细点的最后一张图： 放一个详细点的最后一张图

Batch

这个梯度下降又称为“Batch” gradient Descent

"Batch"：Each step of gradient descent uses all the training examples

指的是每一步都要遍历整个训练集。因为12m∑i=1m(hθ(x(1))−y(i))2\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(1)}\right)-y^{(i)}\right)^{2}公式每一步都要对总体求和。

avatar
文章
阅读
粉丝