/最长公共子序列问题
首先这毫无疑问必然是动态规划,那么首先搞定参数 是两个 是双比较模型, i和j 定义模型的含义,从0到i和0到j 他们有多少个公共子序列,那么参数就会传 两个的长度,这不是从左到右的模型 所以不是固定传0啥的,然后想的就是递推 缩小规模,先想的是basecase 一个字符 或者两个都剩一个字符了,然后讨论情况 是不是以这个i结尾 ,不结尾删了也没事
二维数组雨滴问题
一维的就是双指针 或者找到每个的瓶颈
二维的就是小根堆 跟新最大值 只要是换了最大值就是会了湖泊
其实这个很简单 还是根据算每个点的瓶颈加起来,利用了在没换最大值前 就是还是原来那个湖泊,利用小根堆找到附近能扩到最大的湖泊,一旦更新最大值,头就换了一个,以另一个头部取水
public int trapRainWater(int[][] heightMap) {
if (heightMap == null || heightMap.length == 0 || heightMap[0] == null || heightMap[0].length == 0) {
return 0;
}
int[][]water=new int[heightMap.length][heightMap[0].length];
boolean[][] flag=new boolean[heightMap.length][heightMap[0].length];
int[][]direction=new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
int max=Integer.MIN_VALUE;
PriorityQueue<WaterInfo>queue=new PriorityQueue<>(new Comparator<WaterInfo>() {
@Override
public int compare(WaterInfo o1, WaterInfo o2) {
return o1.value-o2.value;
}
});
for (int i=0;i<heightMap[0].length;i++){
queue.offer(new WaterInfo(heightMap[0][i],0,i));
flag[0][i]=true;
}
for (int i=1;i<heightMap.length-1;i++){
queue.offer(new WaterInfo(heightMap[i][heightMap[0].length-1],i,heightMap[0].length-1));
flag[i][heightMap[0].length-1]=true;
}
for (int i=1;i<heightMap.length-1;i++){
queue.offer(new WaterInfo(heightMap[i][0],i,0));
flag[i][0]=true;
}
for (int i=0;i<heightMap[0].length;i++){
queue.offer(new WaterInfo(heightMap[heightMap.length-1][i],heightMap.length-1,i));
flag[heightMap.length-1][i]=true;
}
while (!queue.isEmpty()){
WaterInfo poll = queue.poll();
max=Math.max(max,poll.value);
water[poll.row][poll.column]=Math.max(0,max-poll.value);
for (int[] i:direction){
int x=poll.row+i[0];
int y=poll.column+i[1];
if (x>=0&&y>=0&&x<heightMap.length&&y<heightMap[0].length&&!flag[x][y]){
queue.offer(new WaterInfo(heightMap[x][y],x,y));
flag[x][y]=true;
}
}
}
/**
* 第一步 先把四周的一圈加入到小更堆
*/
int sum=0;
for (int[]i :water){
for (int j:i){
sum+=j;
}
}
return sum;
}
遇到要求i前面的最大值 可以前缀数组
如果也要i后的最大值 后缀数组就行了 从右往左
二叉树的反序化
就是队列+弹出 然后遇到空就返回
连续循环比较 一定是滑动窗口 一直找到违规位置
题目中又尝试操作且让你求最大最小值必是动态规划
矩阵最大值 等问题最小栈解决 象什么连续最大什么的都是一个套路
位的for循环判断是不是1的两种方式
第一种好一点
public static int hammingWeight(int n) {
int count=0;
for (int i=0;i<32;i++){
if ((n&(1<<i))!=0){
count++;
}
}
return count;
}
public static int hammingWeight(int n) {
int count=0;
for (;n!=0;n>>=1){
if ((n&1)!=0){
count++;
}
}
return count;
}
能用动态规划做的回溯不一定可用回溯是真对要返回数组的 只是计算长度 不准用回溯法
递归开始前用for循环都是要比较的 因为每一个数都要进递归的
计算矩阵中的最长递增子序列 经典
class Solution {
public int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int rows, columns;
public int longestIncreasingPath(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
rows = matrix.length;
columns = matrix[0].length;
int[][] memo = new int[rows][columns];
int ans = 0;
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < columns; ++j) {
ans = Math.max(ans, dfs(matrix, i, j, memo));
}
}
return ans;
}
public int dfs(int[][] matrix, int row, int column, int[][] memo) {
if (memo[row][column] != 0) {
return memo[row][column];
}
++memo[row][column];
for (int[] dir : dirs) {
int newRow = row + dir[0], newColumn = column + dir[1];
if (newRow >= 0 && newRow < rows && newColumn >= 0 && newColumn < columns && matrix[newRow][newColumn] > matrix[row][column]) {
memo[row][column] = Math.max(memo[row][column], dfs(matrix, newRow, newColumn, memo) + 1);
}
}
return memo[row][column];
}
}
数组随机条件场 每个子数组的数目随便
因为要遍历数组且里面的数字是不连续的 用滑动窗口有点困难, 且题目是有条件的满足什么样的数才能放进去
ok 上公式了
这里把这两个加进去是重点
public static List<List<Integer>> threeSumSmaller(int[] nums, int target) {
List<Integer>ans=new ArrayList<>();
List<List<Integer>>res=new ArrayList<>();
process(nums,target,0,ans,res);
return res;
}
private static void process(int[] nums, int target, int index, List<Integer> ans, List<List<Integer>> res) {
if (index==nums.length){
根据题目条件是否加入 然后看他要什么自己处理下就行
if (ans.size()==3){
res.add(new ArrayList<>(ans));
}
return;
}
if (ans.size()==3){
/**
* 加逻辑 根据题目条件是否加
*/
res.add(new ArrayList<>(ans));
return;
}
for (int i=index;i<nums.length;i++){
ans.add(nums[i]);
process(nums,target,i+1,ans,res);
ans.remove(ans.size()-1);
}
}
动态规划怎么想
- 题目中明显是有尝试的
- 数组有子序列的 暴力递归里面加for循环大概率的 以每一个i开始算结果
脑子里面定义好子问题 利用子问题去算答案. 遇到要遍历某一个位子的应该是要加for循环了,就是尝试
记忆化搜索 第一个for循环算的不是动态规划里面的 是处理规划出来的东西,哪一个最长 递归处理的是
当来到i位置的时候,以他为开头最长是多少,对把 但是最长的不一定是以他开头
public static int lengthOfLIS(int[] nums) {
int ans=0;
for (int i=0;i<nums.length;i++){
ans=Math.max(ans,process(nums,i));
}
return ans;
}
private static int process(int[] nums, int i) {
if (i==nums.length){
return 0;
}
int count=0;
for (int j=i+1;j<nums.length;j++){
if (nums[j]>nums[i]){
count=Math.max(count,process(nums,j));
}
}
return ++count;
}
动态规划
public static int lengthOfLIS(int[] nums) {
int[] memory=new int[nums.length];
for (int i=0;i<memory.length;i++){
memory[i]=1;
}
int ans=0;
for (int i= nums.length-1;i>=0;i--){
int count=0;
for (int j=i+1;j<nums.length;j++){
if (nums[j]>nums[i]){
count=Math.max(count,memory[j]);
}
}
memory[i]=++count;
ans=Math.max(ans, memory[i]);
}
return ans;
}
看到找数字想二分
题目中是搜索且空间要求低 就查没直接告诉你用二分了
不用 + 怎么算相加
进位加上不进位相加 异或运算本质就是不进位相加 加上while 循环保证没有进位了 可能两个相加还存在进位
public static int getSum(int a, int b) {
while (b!=0){
int carry=(a&b)<<1;
a=a^b;
b=carry;
}
return a;
}
洗牌算法
原地打乱数组 没到一个位置就交换随机一个index下标
class Solution {
int[]nums;
int[]help;
Random random=new Random();
public Solution(int[] nums) {
this.nums=nums;
help=nums.clone();
}
public int range(int max,int min){
return random.nextInt(max-min)+min;
}
/** Resets the array to its original configuration and return it. */
public int[] reset() {
return nums;
}
public void swap(int[]help ,int i,int j){
int temp=help[i];
help[i]=help[j];
help[j]=temp;
}
/** Returns a random shuffling of the array. */
public int[] shuffle() {
for (int i=0;i<help.length;i++){
swap(help,i,range(help.length,i));
}
return help;
}
}
象什么前k个什么的第一时间想到堆
回溯算法套公式后发现内存溢出 开始改写
public static int longestIncreasingPath(int[][] matrix) {
int[][] direct={{1,0},{-1,0},{0,-1},{0,1},};
boolean[][]help=new boolean[matrix.length][matrix[0].length];
List<Integer> list=new ArrayList<>();
List<List<Integer>>res=new ArrayList<>();
for (int i=0;i<matrix.length;i++){
for (int j=0;j<matrix[0].length;j++){
dps(list,res,matrix,i,j,help,direct);
}
}
int size=1;
for (List<Integer> i:res){
size=Math.max(size,i.size()+1);
}
return size;
}
private static void dps(List<Integer> list, List<List<Integer>> res, int[][] matrix, int i, int j, boolean[][] help, int[][] direct) {
if (!judge(matrix,i,j,help,direct)){
res.add(new ArrayList<>(list));
return;
}
for (int[] index:direct){
int newI=i+index[0];
int newJ=j+index[1];
if (newI>=0&&newJ>=0&&newI<matrix.length&&newJ<matrix[0].length&&!help[newI][newJ]&&
matrix[newI][newJ]>matrix[i][j]){
list.add(matrix[newI][newJ]);
help[newI][newJ]=true;
dps(list,res,matrix,newI,newJ,help,direct);
list.remove(list.size()-1);
help[newI][newJ]=false;
}
}
}
public static boolean judge(int[][] matrix, int i, int j, boolean[][] help, int[][] direct){
for (int[] index:direct){
int newI=i+index[0];
int newJ=j+index[1];
if (newI>=0&&newJ>=0&&newI<matrix.length&&newJ<matrix[0].length&&!help[newI][newJ]&&
matrix[newI][newJ]>matrix[i][j]
){
return true;
}
}
return false;
}
第一题
这一题的暴力方法很好找,就是两个for循环,但是时间都花费再了找第二个数上,如果是数组找数,是有等式的例如相加这种 利用hashmap 非常方便,但是只对两数累加有效果,因为三数累加的时候会改变值,对hanmap改进把数值和value对调 方便拿取 ,做到o(N)对所有值都查一遍,有就找到,没有就放入,无脑。
第三题
public static int lengthOfLongestSubstring(String s) {
int max=0;
HashMap<Character,Integer>map=new HashMap<>();
for (int i=0 , j=0;j<s.length();j++){
if (map.containsKey(s.charAt(j))){
i=Math.max(i,map.get(s.charAt(j))+1);
}
map.put(s.charAt(j),j);
max=Math.max(max,j-i+1);
}
return max;
}
就是利用了hashmap的数组下标计算,两个临近相等字符串长度
第四题
中位数的下标可算 不需要去二分
class Solution {
public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
int l1=nums1.length;
int l2=nums2.length;
boolean flag=false;
int mid=0;
int i=0;
int j=0;
int z=0;
double[] res=new double[l2+l1];
while (i<nums1.length&&j<nums2.length){
if (nums1[i]<=nums2[j]){
res[z++]=nums1[i];
i++;
}
else {
res[z++]=nums2[j];
j++;
}
}
while (j<nums2.length){
res[z++]=nums2[j++];
}
while (i<=nums1.length-1){
res[z++]=nums1[i++];
}
if ((l2+l1)%2==0){
mid=((l2+l1)/2)-1;
return (res[mid]+res[mid+1])/2;
}else {
mid=((l2+l1)/2);
return res[mid];
}
}
第五题
public static String manacher1(String s) {
if (s == null || s.length() == 0) {
return null;
}
// "12132" -> "#1#2#1#3#2#"
char[] str = manacherString(s);
// 回文半径的大小
int[] pArr = new int[str.length];
int C = -1;
// 讲述中:R代表最右的扩成功的位置
// coding:最右的扩成功位置的,再下一个位置
int R = -1;
int max = Integer.MIN_VALUE;
HashMap<Integer,Integer>map=new HashMap<>();
for (int i = 0; i < str.length; i++) { // 0 1 2
// R第一个违规的位置,i>= R
// i位置扩出来的答案,i位置扩的区域,至少是多大。
pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
while (i + pArr[i] < str.length && i - pArr[i] > -1) {
if (str[i + pArr[i]] == str[i - pArr[i]])
{
pArr[i]++;
}
else {
break;
}
}
if (i + pArr[i] > R) {
R = i + pArr[i];
C = i;
}
max=Math.max(max,pArr[i]);
}
int temp=0;
for (int i=0;i< pArr.length;i++){
if (pArr[i]==max){
temp=(i-1)/2;
}
}
int start=0;
int end=0;
if ((max-1)%2==0){
start=(temp-(max-1)/2)+1;
end=(temp+(max-1)/2);
}
else {
start=(temp-(max-1)/2);
end=(temp+(max-1)/2);
}
String substring = s.substring(start, end+1);
return substring;
}
第六题
就是贪心算法 双指针 求最大面级 真是垃圾题目 没意思
第七题
字符串最长前缀和 就比来比去 就行了 。千万别往前缀树那边想
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
String prefix=strs[0];
for (int i=1;i<strs.length;i++){
prefix=longPrefix(prefix,strs[i]);
}
return prefix;
}
private String longPrefix(String prefix, String str) {
int i=0;
int j=0;
while (i<prefix.length()&&j<str.length()){
if (prefix.charAt(i)==str.charAt(j)){
i++;
j++;
}else {
break;
}
}
return prefix.substring(0,i);
}
第七题
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if (n<0||head==null){
return new ListNode();
}
ListNode slow=head;
ListNode quick=head;
for (int i=0;i<n&&quick.next!=null;i++){
quick=quick.next;
}
while (quick.next!=null){
quick=quick.next;
slow=slow.next;
}
if (slow.next!=null){
if (!distence(slow,quick,n)){
return head.next;
}
else {
slow.next=slow.next.next;
return head;
}
}
else {
return null;
}
}
private boolean distence(ListNode slow, ListNode quick, int n) {
int count=0;
for (int i=0;i<n;i++){
slow=slow.next;
count++;
if (slow==quick){
break;
}
}
return count==n;
}
}
第八题
class Solution {
public boolean isValid(String s) {
if (s==null||s.length()<1){
return false;
}
Stack<Character>stack=new Stack<>();
HashMap<Character,Character>map=new HashMap<>();
map.put('(',')');
map.put('{','}');
map.put('[',']');
map.put(')','1');
map.put('}','2');
map.put(']','3');
char[] chars = s.toCharArray();
for (int i=0;i<chars.length;i++){
if (stack.isEmpty()){
stack.push(chars[i]);
}
else {
if (chars[i]==map.get(stack.peek())){
stack.pop();
}
else {
stack.push(chars[i]);
}
}
}
if (stack.isEmpty()){
return true;
}
return false;
}
}
第9题
就是范围性的尝试,我计算出的第一个点+ 后面计算好的点 而且一定要用next把链表连起来
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1==null){
return l2;
}
else if (l2==null){
return l1;
}
else if (l1.val<= l2.val){
l1.next=mergeTwoLists(l1.next,l2);
return l1;
}
else {
l2.next=mergeTwoLists(l1,l2.next);
return l2;
}
}
第10题
注意等号的位置 要确保能取到边界值 不象以前一直向一边移动,这次可能向两边移动
public int search(int[] nums, int target) {
int n = nums.length;
if (n == 0) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int i=0;
int j=n-1;
while (i<=j){
int mid=i+((j-i)>>1);
if (nums[mid]==target){
return mid;
}
if (nums[mid]>=nums[0]){
if (nums[0]<=target&&target<nums[mid]){
j=mid-1;
}else {
i=mid+1;
}
}else {
if (nums[mid]<target&&target<=nums[n-1]){
i=mid+1;
}else {
j=mid-1;
}
}
}
return -1;
}
第11题
这题就是标准的二分找边界值问题 找到了这个值然后向两边扩展,注意边界值取值就行了
public int[] searchRange(int[] nums, int target) {
if (nums==null||nums.length==0){
return new int[]{-1,-1};
}
int n= nums.length;
int i=0;
int j=n-1;
int mid;
while (i<=j){
mid=i+((j-i)>>1);
if (nums[mid]==target){
return process(nums,target,mid);
}
else if (target>=nums[mid]){
i=mid+1;
}
else {
j=mid-1;
}
}
return new int[]{-1,-1};
}
private int[] process(int[] nums, int target, int mid) {
int i=mid;
int j=mid;
while (i>0&&j< nums.length-1&&nums[--i]==target&&nums[++j]==target){
}
while (i>0&&nums[i]==target){
i--;
}
while (j< nums.length-1&&nums[j]==target){
j++;
}
if (i==j||(i==0&&j== nums.length-1&&nums[i]==target&&nums[j]==target)){
return new int[]{i,j};
}
else if (i==0&&nums[j]!=target&&nums[i]==target){
return new int[]{i,j-1};
}
else if (nums[i]!=target&&j== nums.length-1&&nums[j]==target){
return new int[]{i+1,j};
}
else {
return new int[]{i+1,j-1};
}
第12题
回溯算法的应用,用过的数字不能再用了,for循环的i是必须的变的 不然就重复了,
public List<List<Integer>> permute(int[] nums) {
if (nums==null||nums.length==0){
return null;
}
int n=nums.length;
List<List<Integer>>res=new ArrayList<>();
List<Integer>output=new ArrayList<>();
for (int i:nums){
output.add(i);
}
backtrack(res,output,n,0);
return res;
}
private void backtrack(List<List<Integer>> res, List<Integer> output, int n, int index) {
if (index==n){
res.add(new ArrayList<>(output));
}
for (int i=index;i<n;i++){
Collections.swap(output,i,index);
backtrack(res,output,n,index+1);
Collections.swap(output,i,index);
}
}
}
第13题 小贪心
子数组最大和 只要是前累加和是小于0的直接舍弃 重新开始
public int maxSubArray(int[] nums) {
if (nums==null||nums.length==0){
return 0;
}
int max=nums[0];
int pre=0;
for (int i=0;i<nums.length;i++){
// pre=Math.max(nums[i],nums[i]+pre );
if (pre<0){
pre=nums[i];
}
else {
pre=pre+nums[i];
}
max=Math.max(max,pre);
}
return max;
}
}
第14题
class Solution {
public int climbStairs(int n) {
if (n < 1) {
return 0;
}
if (n == 1 ) {
return 1;
}
if(n==2){
return 2;
}
// [ 1 ,1 ]
// [ 1, 0 ]
int[][] base = {
{ 1, 1 },
{ 1, 0 }
};
int[][] res = matrixPower(base, n - 1);
return res[0][0] + res[1][0];
}
public int[][] matrixPower(int[][] m, int p) {
int[][] res = new int[m.length][m[0].length];
for (int i = 0; i < res.length; i++) {
res[i][i] = 1;
}
// res = 矩阵中的1
int[][] t = m;// 矩阵1次方
for (; p != 0; p >>= 1) {
if ((p & 1) != 0) {
res = muliMatrix(res, t);
}
t = muliMatrix(t, t);
}
return res;
}
// 两个矩阵乘完之后的结果返回
public int[][] muliMatrix(int[][] m1, int[][] m2) {
int[][] res = new int[m1.length][m2[0].length];
for (int i = 0; i < m1.length; i++) {
for (int j = 0; j < m2[0].length; j++) {
for (int k = 0; k < m2.length; k++) {
res[i][j] += m1[i][k] * m2[k][j];
}
}
}
return res;
}
}
第15题 矩阵轨迹问题
关键在于画点找轨迹 不能执着于点位置的变化
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> list = new ArrayList<>();
int lr = 0;
int lc = 0;
int rr = matrix.length - 1;
int rc = matrix[0].length - 1;
while (lr <= rr && lc <= rc) {
printCircle(matrix, lr++, lc++, rr--, rc--, list);
}
return list;
}
private void printCircle(int[][] matrix, int a, int b, int c, int d, List<Integer> list) {
if (a==c){
for (int i=b;i<=d;i++){
list.add(matrix[a][i]);
}
}
else if (b==d){
for (int i=a;i<=c;i++){
list.add(matrix[i][b]);
}
}
else {
int curRow=a;
int curCol=b;
while (curCol!=d){
list.add(matrix[a][curCol++]);
}
while (curRow!=c){
list.add(matrix[curRow++][d]);
}
while (curCol!=b){
list.add(matrix[c][curCol--]);
}
while (curRow!=a){
list.add(matrix[curRow--][b]);
}
}
}
}
第16题 回溯法 删不是换
public static List<List<Integer>> subsets(int[] nums) {
List<List<Integer>>res=new ArrayList<>();
List<Integer>list=new ArrayList<>();
process(nums,0,res,list);
return res;
}
private static void process(int[] nums, int i, List<List<Integer>> res, List<Integer> list) {
if (i== nums.length){
res.add(new ArrayList<>(list));
return;
}
res.add(new ArrayList<>(list));
for (int index=i;index<nums.length;index++){
list.add(nums[index]);
process(nums,index+1,res,list);
list.remove(list.size()-1);
}
}
回溯算法
找到就break返回 没找到继续上下左右来来回回
public boolean exist(char[][] board, String word) {
int n=board.length;
int m=board[0].length;
boolean[][] help=new boolean[n][m];
for (int i=0;i<n;i++){
for (int j=0;j<m;j++){
boolean flag= check(board,word,help,0,i,j);
if (flag) {
return true;
}
}
}
return false;
}
private boolean check(char[][] board, String word, boolean[][] help, int length, int i, int j) {
if (board[i][j]!=word.charAt(length)){
return false;
}else if (length==word.length()-1){
return true;
}
int[][] direction={{0,1},{1,0},{-1,0},{0,-1}};
help[i][j]=true;
boolean flag=false;
for (int[] dire:direction){
int newi=i+dire[0];
int newj=j+dire[1];
if (newi>=0&&newj>=0&&newi< board.length&&newj<board[0].length&&!help[newi][newj]){
flag=check(board,word,help,length+1,newi,newj);
if (flag){
break;
}
}
}
help[i][j]=false;
return flag;
}
单挑栈
因为面级最大就是扩展 具体就是到第一个违规的地方 所有找的是两边最小 不是两边最大
public int largestRectangleArea(int[] heights) {
Stack<Integer>stack=new Stack<>();
int max=0;
for (int i=0;i<heights.length;i++){
if (stack.isEmpty()){
stack.push(i);
}else {
while (!stack.isEmpty()&&heights[i]<heights[stack.peek()]){
Integer pop = stack.pop();
if (stack.isEmpty()){
max=Math.max(max,(i)*heights[pop]);
}
else {
max=Math.max(max,(i-stack.peek()-1)*heights[pop]);
}
}
stack.push(i);
}
}
while (!stack.isEmpty()){
int r=heights.length;
Integer pop = stack.pop();
max=stack.isEmpty()?Math.max(max,r*heights[pop]):Math.max(max,(r-stack.peek()-1)*heights[pop]);
}
return max;
}
字符串中找到出现字母最短串
第一段:用滑动窗口,当出现全部字母时窗口形成 第二段:窗口前缩到最短包含 第三段:窗口放弃一个字母 继续前进搜索下一个字母
合并区间
用array的特性去sort 用比较器,最后在转化回来 merged.toArray(new int[merged.size()][]);
然后就是看当前区间的左如果在数组中最后一个右端点的右边不可能重合,反之如果重合 去最大值
二叉树不按照套路的
因为是要向两边要却不一样的信息,没有统一的信息
public boolean isSymmetric(TreeNode root) {
return check(root,root);
}
private boolean check(TreeNode root, TreeNode root1) {
if (root==null&&root1==null){
return true;
}
if (root==null||root1==null){
return false;
}
return root.val==root1.val&&check(root.left,root1.right)&&check(root.right,root1.left);
}
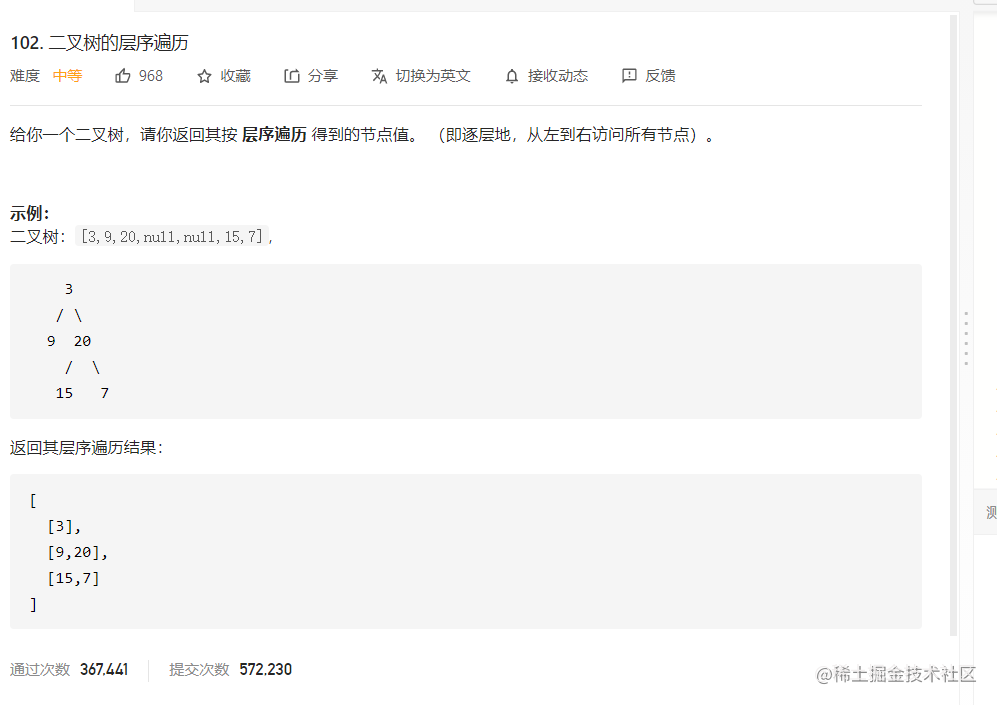
二叉树按层遍历怎么记录没层的数量
细节就是用当前的queue的size() 提前设置好,当该层扔完了,然后重新计算
public List<List<Integer>> levelOrder(TreeNode root) {
if (root==null){
return new ArrayList<>();
}
List<List<Integer>>res=new ArrayList<>();
Queue<TreeNode>queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int currentSize=queue.size();
List<Integer> list=new ArrayList<>();
for (int i=0;i<currentSize;i++){
TreeNode poll = queue.poll();
list.add(poll.val);
if (poll.left!=null){
queue.offer(poll.left);
}
if (poll.right!=null){
queue.offer(poll.right);
}
}
res.add(new ArrayList<>(list));
}
return res;
}
简单回文新思路
利用stringbuild 的reverse函数直接翻一下对比 ,加上字符的处理函数简直不要太爽 且全部变成小写对比 真是无敌
public boolean isPalindrome(String s) {
StringBuilder str=new StringBuilder();
int n=s.length();
for (int i=0;i<s.length();i++){
char c = s.charAt(i);
if (Character.isLetterOrDigit(c)){
str.append(Character.toLowerCase(c));
}
}
String s1 = str.toString();
return s1.equals(str.reverse().toString());
}
二叉树最大路径和问题 套路解决不了
看该点的左右选一个 然后更新所有值 左加右+当前的值,可以去0的
用hashmap检验环形列表
public boolean hasCycle(ListNode head) {
Set<ListNode> seen = new HashSet<ListNode>();
while (head != null) {
if (!seen.add(head)) {
return true;
}
head = head.next;
}
return false;
}
递归生成二叉树
套路都差不多的 先构建根节点 然后 左右节点 往递归里面传
public TreeNode sortedArrayToBST(int[] nums) {
if (nums==null){
return null;
}
return process(nums,0,nums.length-1);
}
private TreeNode process(int[] nums, int start, int end) {
if (start>end){
return null;
}
int mid=start+((end-start)>>1);
TreeNode root=new TreeNode(nums[mid]);
root.left=process(nums,start,mid-1);
root.right=process(nums,mid+1,end);
return root;
}
经典动态规划
关键就是这个决定要的东西需要加上去的不是你参数上加上就好了,
public static int rob(int[] nums) {
if (nums==null){
return 0;
}
int sum=0;
for (int i:nums){
sum+=i;
}
int[][]dp=new int[nums.length+1][sum+1];
for (int i=0;i< dp.length;i++){
for (int j =0;j<dp[0].length;j++){
dp[i][j]=-1;
}
}
return process(nums,0,0,dp);
}
private static int process(int[] nums, int i, int money,int[][]dp) {
if (i>= nums.length){
return 0;
}
if (dp[i][money]!=-1){
return dp[i][money];
}
int p1 = process(nums, i + 1, money,dp);
int p2=0;
if (i+1<=nums.length){
int next = process(nums, i + 2, money + nums[i],dp);
p2=next+nums[i];
}
dp[i][money]=Math.max(p1,p2);
return dp[i][money];
}
自己写的反转列表秒杀全部人
想不到retuen啥 就直接把process返回
class Solution {
public static ListNode reverseList(ListNode head) {
ListNode process = process(null, head);
return process;
}
private static ListNode process(ListNode pre,ListNode cur) {
if (cur==null){
return pre;
}
ListNode temp= cur.next;
cur.next=pre;
return process(cur,temp);
}
}
简简单单异或
public int singleNumber(int[] nums) {
int a=0;
for (int i:nums){
a^=i;
}
return a;
}
投票机制
因为题目要求了是大于一半 所有这个数的票数必然是最多的 所有票数多了就换人就好了。
public int majorityElement(int[] nums) {
int count=0;
int people=nums[0];
for (int i=0;i<nums.length;i++){
if (nums[i]==people){count++;}
else {
--count;
if (count<0&&nums[i]!=people){
people=nums[i];
count=1;
}
}
}
return people;
}
数组交集 什么相交之类的可以先考虑hashmap
用hashmap就行
融合大法 回溯加上动态规划
遍历加上回溯 我要这个或者这个 假设到index我会有很多可能性,都试一下, 看这个是不是回文直接就用动态规划
List<List<String>>res=new ArrayList<>();
List<String>ans=new ArrayList<>();
int n;
int[][]dp;
public List<List<String>> partition(String s) {
if(s.length()<1){
return null;
}
dp=new int[s.length()+1][s.length()+1];
n=s.length();
dfs(s,0);
return res;
}
private void dfs(String s, int i) {
if (i==n){
res.add(new ArrayList<>(ans));
return;
}
for (int j=i;j<s.length();j++){
if (isPalindrome(s,i,j)==1){
ans.add(s.substring(i,j+1));
dfs(s,j+1);
ans.remove(ans.size()-1);
}
}
}
private int isPalindrome(String s, int i, int j) {
if (dp[i][j]!=0){
return dp[i][j];
}
if (i>=j){
dp[i][j]=1;
return 1;
}
else if (s.charAt(i)!=s.charAt(j)){
dp[i][j]=-1;
return -1;
}
dp[i][j]= isPalindrome(s,i+1,j-1);
return dp[i][j];
}
矩阵改值但是会影响结果的 用特殊法
用特殊字符或者是 -1 2这中不影响结果的。
会议室问题和衍生问题
解决会议室问题需要用到堆 但需要手动的该值和获取全部的数据用自己写的堆会好一点 参数一般为数组 当遇到,有尝试类型的就直接上递归了没办法了。
多数组求和问题等于0
可用用hashmap来求负数 对半开 遍历完后map不用把数据删除
判断是不是每个数的幂次方
先模 然后除以这个数看是不是等于1 因为有些不是幂次方也能模的