CSS Matrix 变换原理

2021年04月02日 02:37 · 阅读 908

矩阵乘法

也叫「点积」，AxB=C 的算法如下

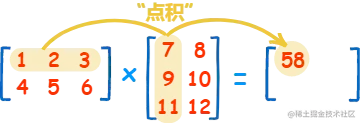
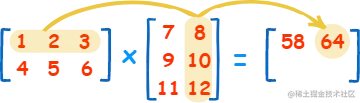
规则：

这玩意有什么用？

假设我们有一个 1x1 的正方形，左下角正好在原点上：

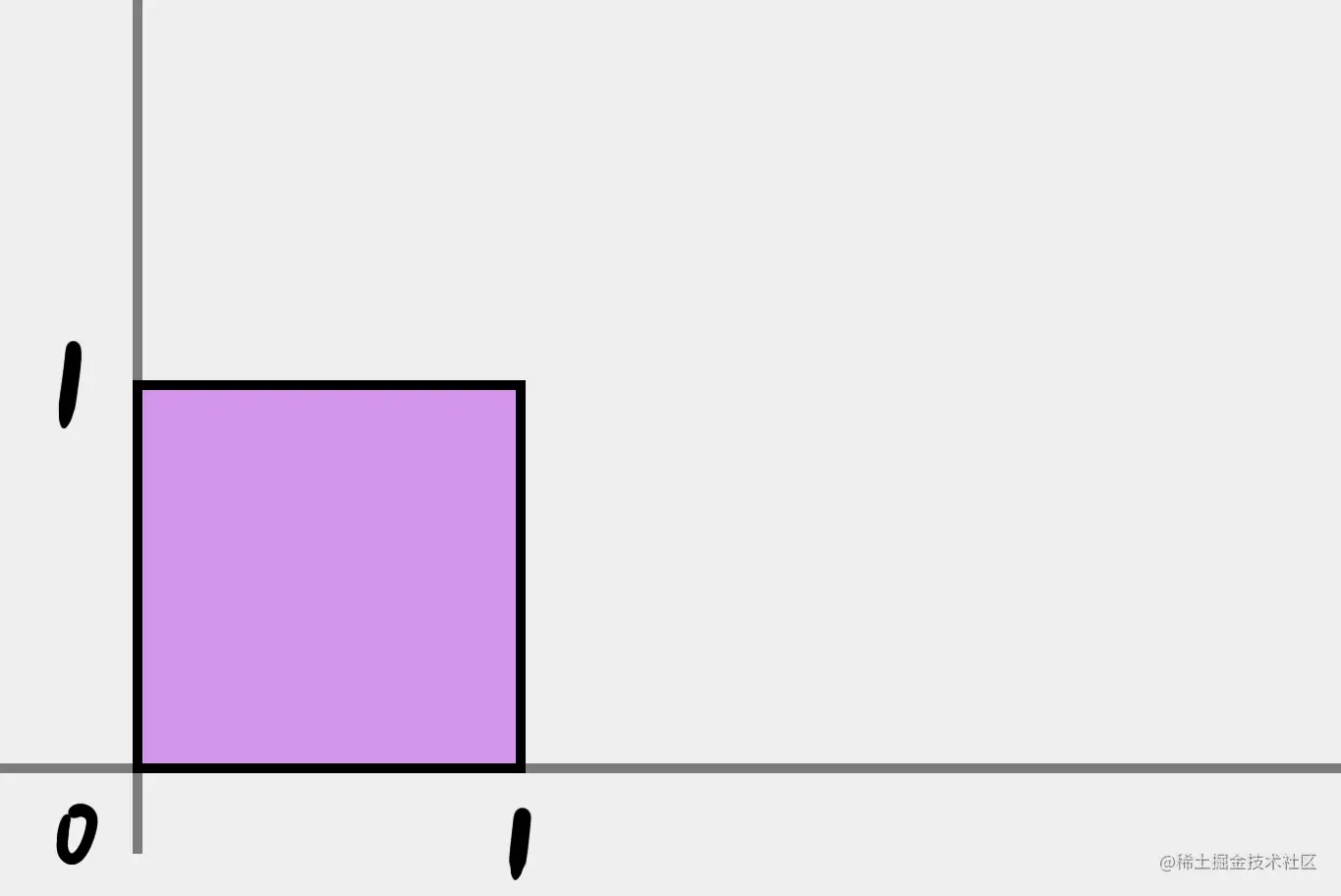
我想把它放大两倍，变成这样：

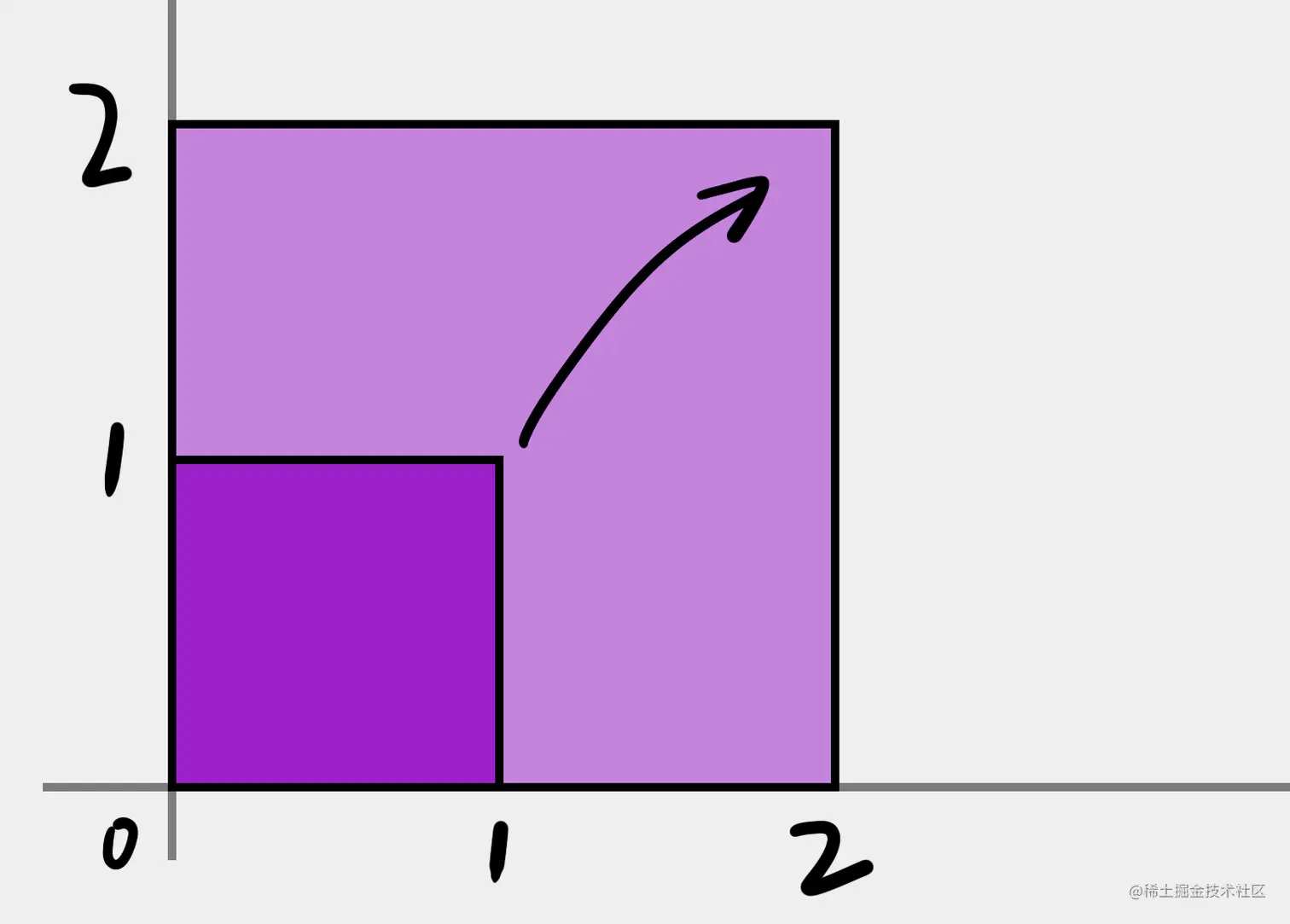
应该怎么做？

\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix} = \begin{bmatrix} 2x+0y & 0x + 2y \end{bmatrix} = \begin{bmatrix} 2x & 2y \end{bmatrix}

各顶点的变化如下：

如果我只延长 x 呢？如下：

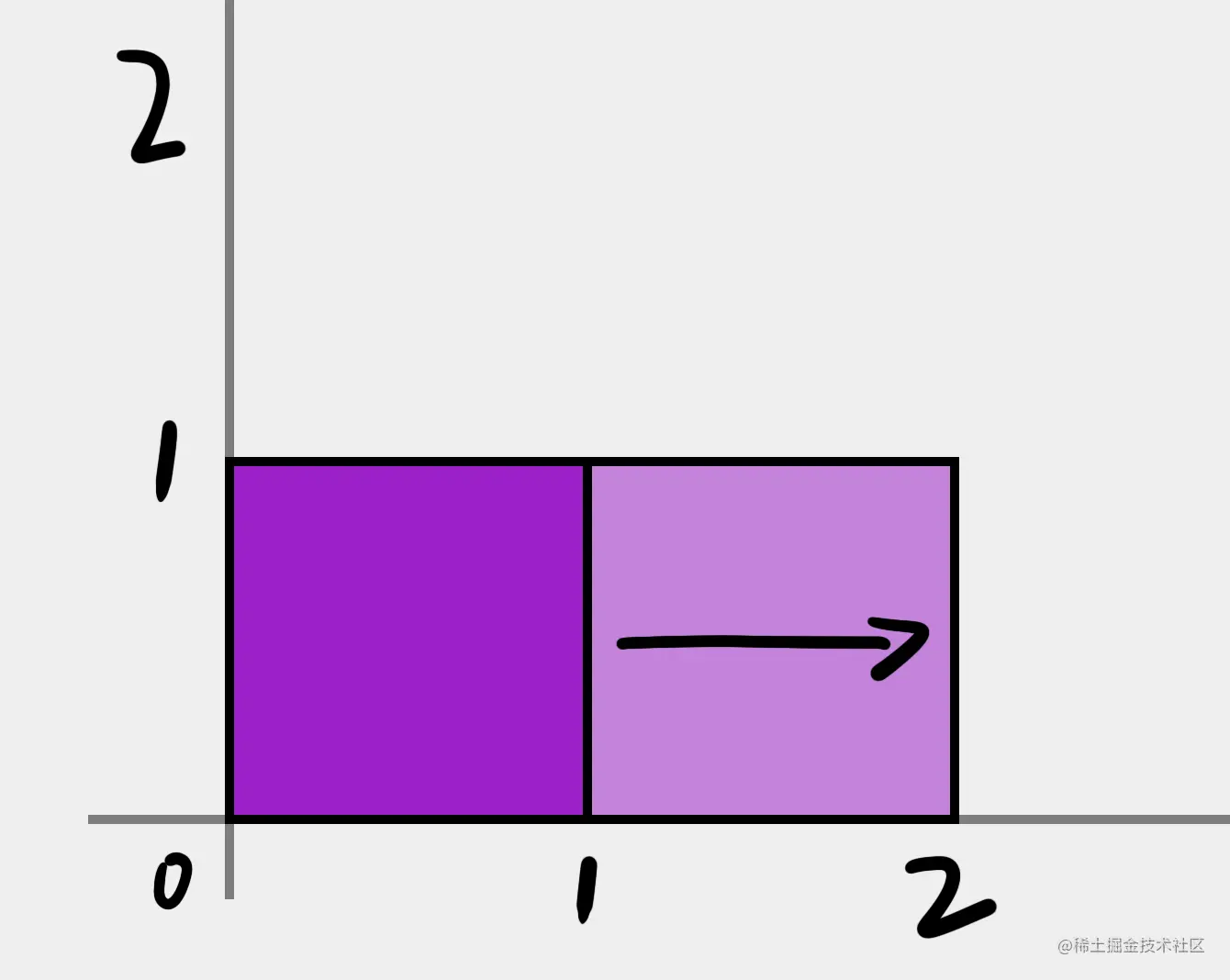
应该怎么做？

\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 2 & 0\\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2x & y \end{bmatrix}

各顶点的变化如下：

至此，我们发现

\begin{bmatrix} 2表示x的变化 & 0\\ 0 & 1表示y不变 \end{bmatrix}

如果随着 x 的增长，y 在慢慢增长呢？

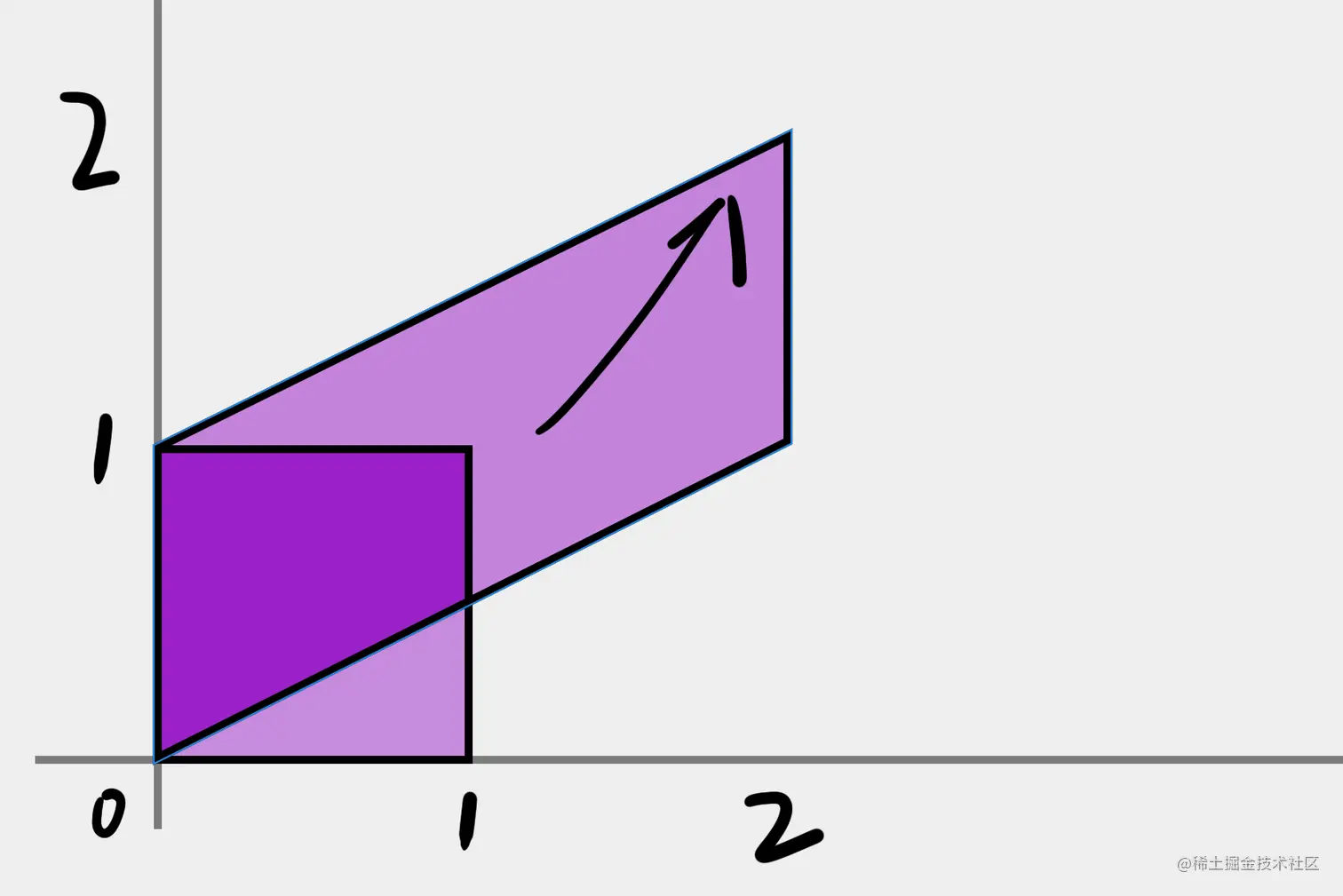
怎么做？

\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 2 & 1\\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2x & x+y \\ \end{bmatrix}

各顶点的变化如下：

至此，我们发现右上角的 1 表示，在 x 变化时，y 的增量。这个量再加上 y 本身的量，就得到了 x + y。

同理，左下角的 0 表示 y 变化时，x 的增量。

比如

\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 2 & 0\\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 2x+y & y \\ \end{bmatrix}

各顶点的变化如下：

把点连起来，得到的图形是：

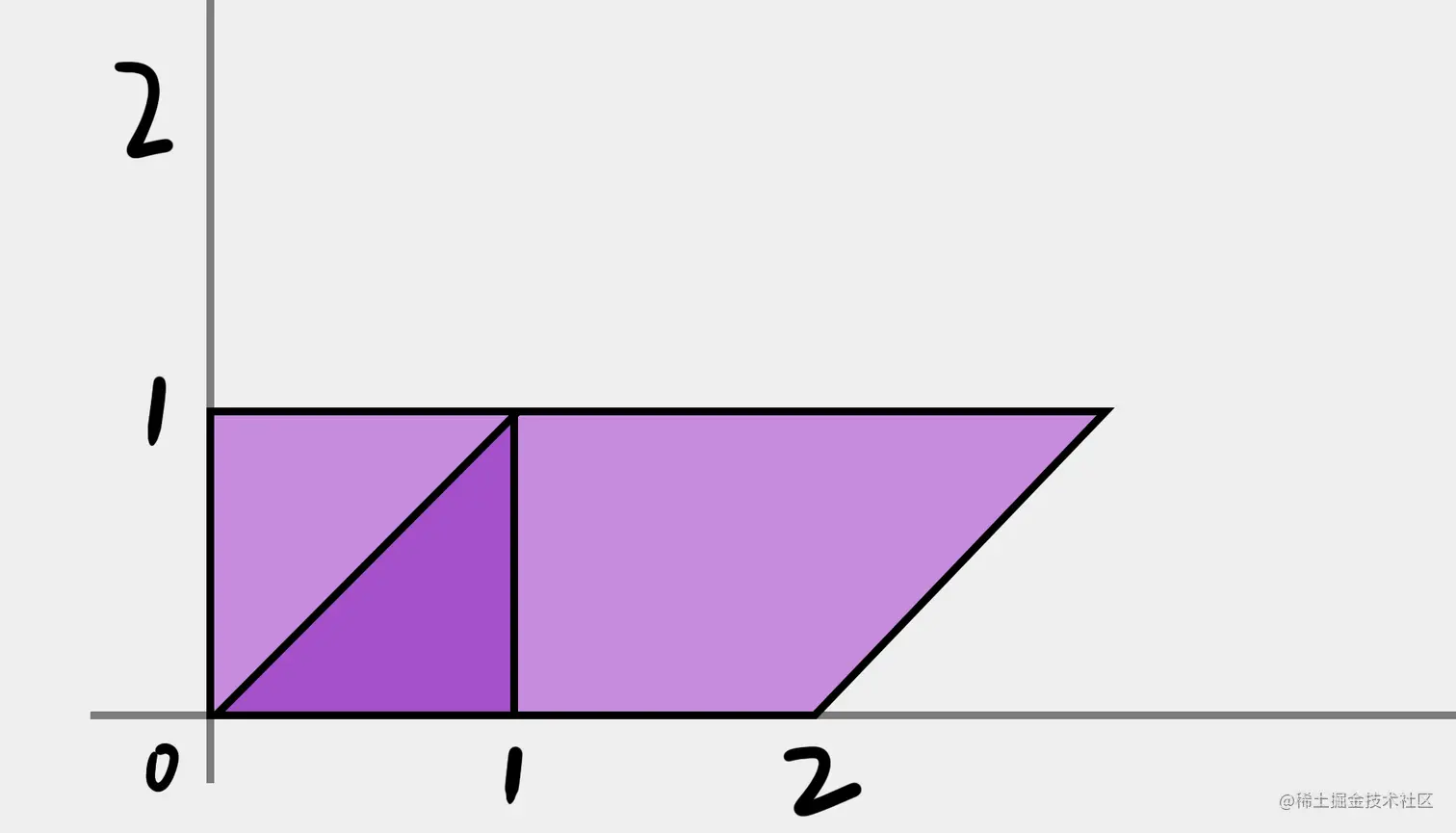
这说明方形除了在 x 方向变为两倍以外，还向 y 方向倾斜了 45 度。

至此，我们发现

\begin{bmatrix} x在x轴的变化量 & y在x轴的变化量\\ x在y轴的变化量 & y在y轴的变化量 \end{bmatrix}

用更简单的符号表示就是：

\begin{bmatrix} x=>x轴 & y=>x轴 \\ x=>y轴 & y=>y轴 \end{bmatrix}

至此，我们知道方形的缩放和倾斜如何用矩阵乘法表示，那么平移怎么表示呢？

平移是不是直接加在最终 (x,y) 上的两个量？

那么我们把矩阵扩展一下：

\begin{bmatrix} x=>x轴 & y=>x轴 \\ x=>y轴 & y=>y轴 \\ x固定增量 & y固定增量 \end{bmatrix}

这样一来是不是就能平移 x 和 y？

但是回顾前面的规则：

当 A 的列数等于 B 的行数时，A 与 B 才可以相乘

如果我们增加了 B 的行数，就必须增加 A 的列数了，所以我们不得不在 x y 后面加个 1

\begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & 1 \\ 10 & 10 \end{bmatrix} = \begin{bmatrix} x+10 & y+10 \\ \end{bmatrix}

但是 (x,y,1) 变成 (x+10,y+10) 后为什么会少了一位呢？为了让两边的列数相等（只是为了对称美），我们干脆再给 B 加一列：

\begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 10 & 10 & 1 \end{bmatrix} = \begin{bmatrix} x+10 & y+10 & 1 \\ \end{bmatrix}

好了，这样我们就成功得把 (x,y,1) 变成了 (x+10,y+10,1)，也就是向 x、y 方向分别平移了 10 像素！

那么绕自身中心顺时针旋转 45 度怎么实现呢？

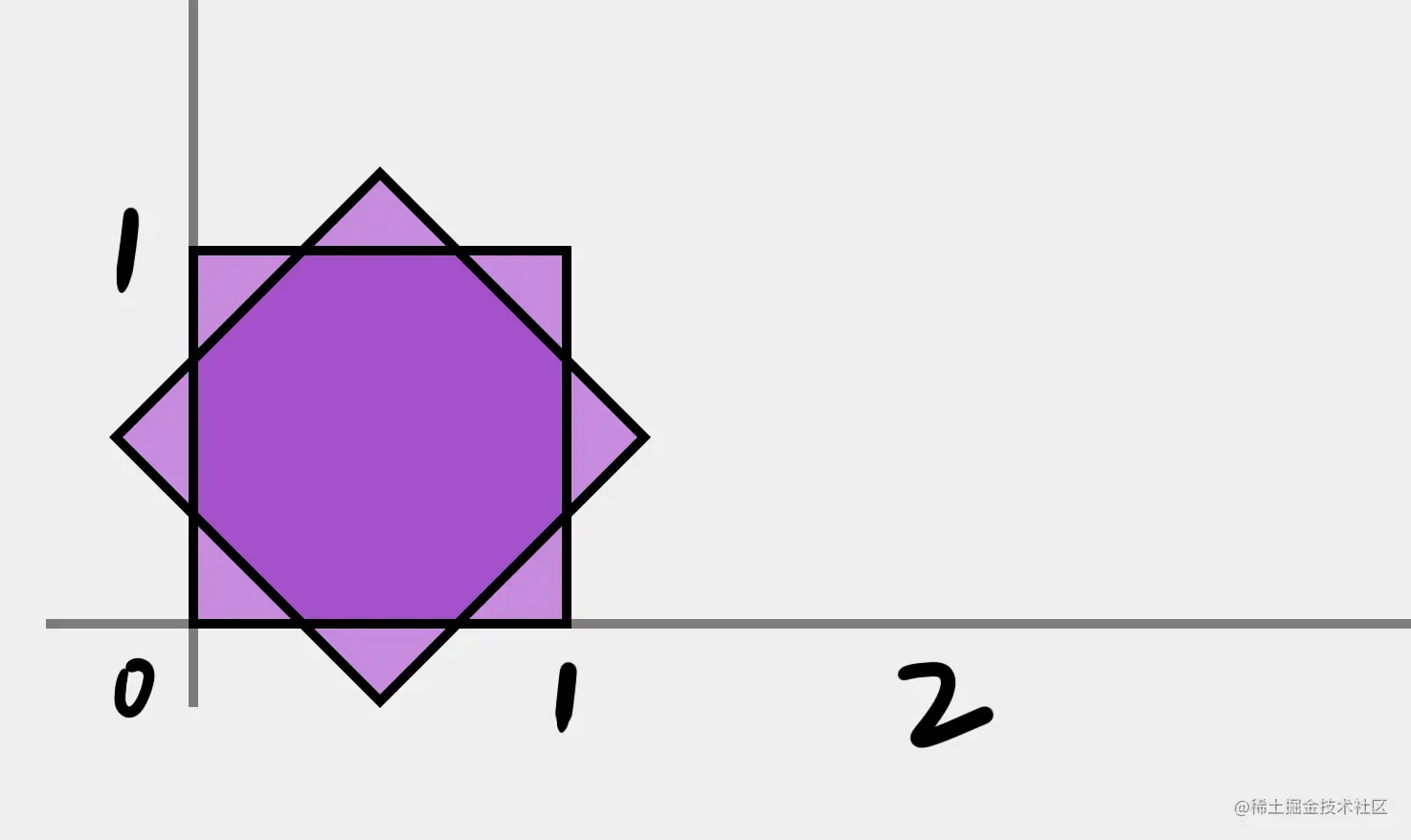
看起来 x、y 的变化与旋转的角度有关，肯定要用到 sin / cos 这样的三角函数了，细节我们就不推了（我不会），但可以肯定的是，目前的 3x3 矩阵肯定是可以做到旋转变换。

同理，如果要对 (x,y,z) 进行变换，则需要一个 4x4 的矩阵进行乘法运算。

这就是 CSS Matrix 3D 变换的原理，你学废了吗？