机器学习算法之朴素贝叶斯

万里独行田伯光
622 阅读3分钟

算法简介

根据李航《统计学习方法》这本书的描述，机器学习算法，可以分为概率模型和非概率模型。这本书所提到的两个分类所包含的模型如下：

  • 概率模型 包括决策树、朴素贝叶斯、隐马尔科夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型是概率模型。
  • 非概率模型 包括感知机、支持向量机、k近邻、AdaBoost、k均值、潜在语义分析以及神经网络算法。

此外 逻辑回归，既可以看做概率模型，也可以看做非概率模型。

以上概率模型中，之前已经描述过决策树模型，今天我们来讲讲朴素贝叶斯分类。

朴素贝叶斯，是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设，学习输入输出的联合概率分布；然后基于此模型，对于给定的输入，利用贝叶斯定理求出后验概率最大的输出。该算法实现简单，学习与预测的效率都很高，是一种常用的方法。

我们先复习一下基本的概率论的知识

概率论基础知识

贝叶斯公式
P(Bi∣A)=P(A∣Bi)⋅P(Bi)∑j=1nP(A∣Bi)⋅P(Bi)P(B_i | A) = \frac {P(A | B_i) · P(B_i)} { \sum _{j=1} ^{n} {P(A | B_i) · P(B_i)} }

这里的分母其实就是P(A)P(A)

如果对贝叶斯公式不理解的，我们可以看一个简化版的：

P(B∣A)=P(A∣B)⋅P(B)P(A)P(B | A) = \frac {P(A | B) · P(B)} {P(A)}

下面这个图有助于我们理解这个公式：

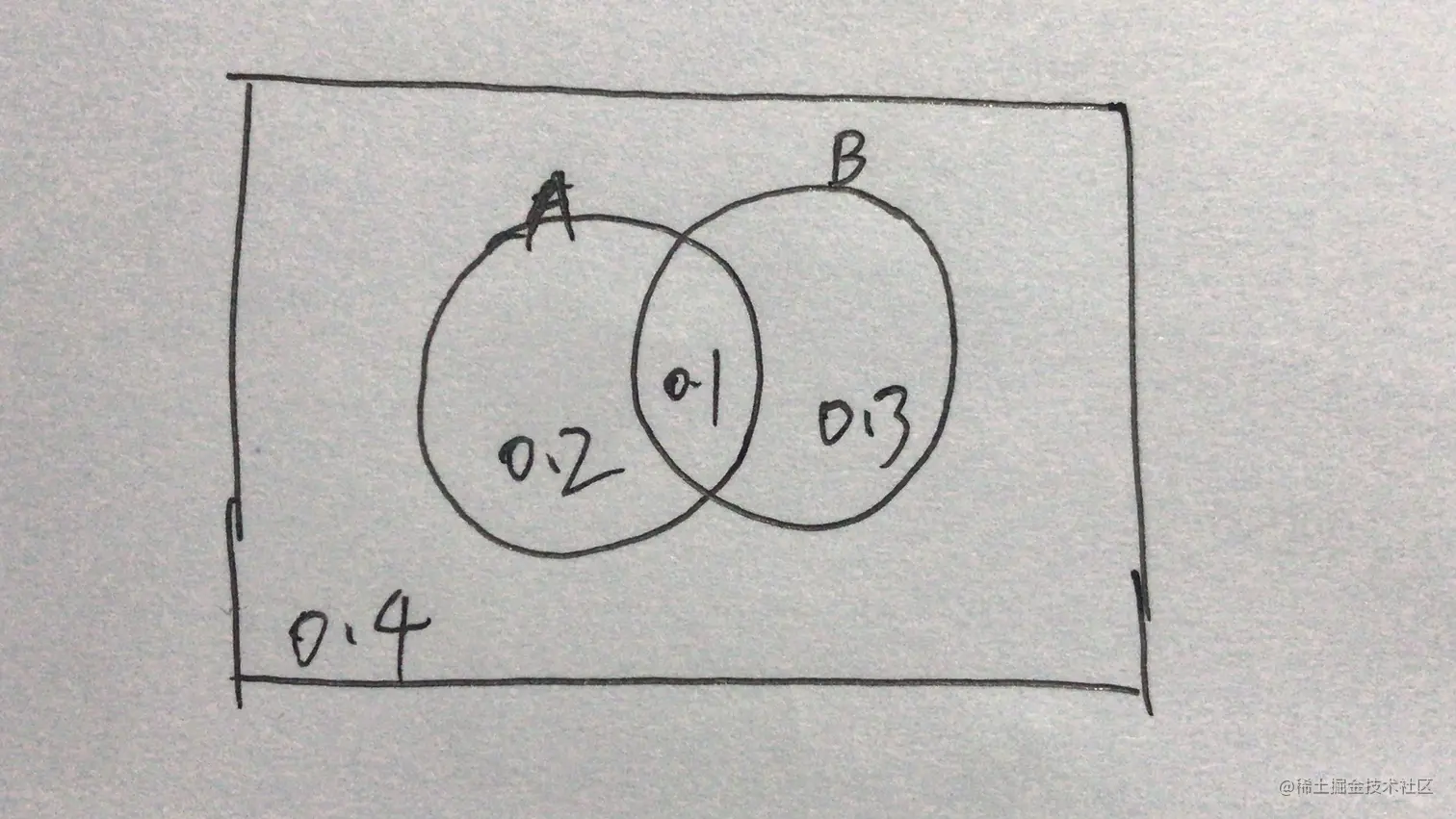
$P(B | A) 就是A条件下，B发生的概率。 A 表示左边的圈，概率是0.3；B表示右边的圈，概率是0.4；矩形表示所有可能性的集合，概率是1。 其中

P(A)=0.3P(A) = 0.3
P(B)=0.4P(B) = 0.4

两个圈的交集，就是表示AB同时发生的概率：

P(AB)=0.1P(AB) = 0.1

公式的左边

P(B∣A)=1/3=0.33333...P(B|A) = 1 / 3 = 0.33333...

公式的右边

P(A∣B)⋅P(B)P(A)=0.10.40.40.3=1/3=0.33333...\frac {P(A|B) · P(B)} {P(A)} = \frac {\frac {0.1} {0.4} 0.4 } {0.3} = 1 / 3 = 0.33333...

发现公式是刚好成立的。

本文我们来看一个分类问题。

算法场景

有如下数据集，X1X_1 和 X2X_2是特征集，取值集合 A1={1,2,3}A_1 = \{1,2,3\}，A2={S,M,L}A_2 = \{S, M, L\}，YY为类标记，Y∈C={1,−1}Y\in C = \{1, -1\}。

训练数据如下：

X1X_1X2X_2YY
11S-1
21M-1
31M1
41S1
51S-1
62S-1
72M-1
82M1
92L1
102L1
113L1
123M1
133M1
143L1
153L-1

给定新样本 (2, S)，求该样本的预测值。

这个问题乍一看，可以看到表格中有一个样本就是(2, S)。那么直接查表，结果不就是 -1 吗？这种想法对吗？ 不对！很直接的一个原因，因为这里的target值都是概率性的，同样的条件，有一定的概率得到-1， 或 1 。这里根据特征(2, S)，表格中恰好得到了 -1。并不表示根据特征(2, S) 得到target=-1的概率是100%。

结果预测

根据上述样本可以计算得到以下概率：

P(Y=1)=915,P(Y=−1)=615P(Y=1) = \frac {9} {15}, P(Y = -1) = \frac {6} {15}

P(X(1)=1∣Y=1)=29,P(X(1)=2∣Y=1)=39,P(X(1)=3∣Y=1)=49,P(X^{(1)} = 1 | Y = 1) = \frac {2} {9}, P(X^{(1)} = 2 | Y = 1) = \frac {3} {9}, P(X^{(1)} = 3 | Y = 1) = \frac {4} {9},

P(X(2)=S∣Y=1)=19,P(X(2)=M∣Y=1)=49,P(X(2)=L∣Y=1)=49,P(X^{(2)} = S | Y = 1) = \frac {1} {9}, P(X^{(2)} = M | Y = 1) = \frac {4} {9}, P(X^{(2)} = L | Y = 1) = \frac {4} {9},

P(X(1)=1∣Y=−1)=36,P(X(1)=2∣Y=−1)=26,P(X(1)=3∣Y=−1)=16,P(X^{(1)} = 1 | Y = -1) = \frac {3} {6}, P(X^{(1)} = 2 | Y = -1) = \frac {2} {6}, P(X^{(1)} = 3 | Y = -1) = \frac {1} {6},

P(X(2)=S∣Y=−1)=36,P(X(2)=M∣Y=−1)=26,P(X(2)=L∣Y=−1)=16,P(X^{(2)} = S | Y = -1) = \frac {3} {6}, P(X^{(2)} = M | Y = -1) = \frac {2} {6}, P(X^{(2)} = L | Y = -1) = \frac {1} {6},

对于给定的 (2, S)，我们分别计算它预测为1 和-1 的概率。

结果为1的概率：

P(Y=1∣X(1)=2,X(2)=S)P(Y = 1 | X^{(1)} = 2, X^{(2)} = S )

=P(X(1)=2,X(2)=S∣Y=1)⋅P(Y=1)P(X(1)=2,P(X(2)=S)= \frac {P(X^{(1)} = 2, X^{(2)} = S | Y = 1 ) · P(Y = 1)} {P(X^{(1)} = 2, P(X^{(2)} = S) }

=P(X(1)=2∣Y=1)P(X(2)=S∣Y=1)⋅P(Y=1)P(X(1)=2,X(2)=S)=39⋅19⋅915P(X(1)=2,P(X(2)=S)=145⋅P(X(1)=2,P(X(2)=S)= \frac {P(X^{(1)} = 2 | Y = 1 ) P(X^{(2)} = S | Y = 1 ) · P(Y = 1)} {P(X^{(1)} = 2, X^{(2)} = S) } = \frac {\frac {3} {9} ·\frac {1} {9} · \frac {9} {15} } {P(X^{(1)} = 2, P(X^{(2)} = S) } = \frac {1} {45 ·{P(X^{(1)} = 2, P(X^{(2)} = S) }}

结果为-1 的概率：

P(Y=−1∣X(1)=2,X(2)=S)P(Y = -1 | X^{(1)} = 2, X^{(2)} = S )

=P(X(1)=2,X(2)=S∣Y=−1)⋅P(Y=−1)P(X(1)=2,P(X(2)=S)= \frac {P(X^{(1)} = 2, X^{(2)} = S | Y = -1 ) · P(Y = -1)} {P(X^{(1)} = 2, P(X^{(2)} = S) }

=P(X(1)=2∣Y=−1)P(X(2)=S∣Y=−1)⋅P(Y=−1)P(X(1)=2,X(2)=S)=26⋅36⋅615P(X(1)=2,P(X(2)=S)=115⋅P(X(1)=2,P(X(2)=S)= \frac {P(X^{(1)} = 2 | Y = -1 ) P(X^{(2)} = S | Y = -1 ) · P(Y = -1)} {P(X^{(1)} = 2, X^{(2)} = S) } = \frac {\frac {2} {6} ·\frac {3} {6} · \frac {6} {15} } {P(X^{(1)} = 2, P(X^{(2)} = S) } = \frac {1} {15 ·{P(X^{(1)} = 2, P(X^{(2)} = S) }}

对比可以得到

P(Y=−1∣X(1)=2,X(2)=S)>P(Y=1∣X(1)=2,X(2)=S)P(Y = -1 | X^{(1)} = 2, X^{(2)} = S ) > P(Y = 1 | X^{(1)} = 2, X^{(2)} = S )

所以(2, S)的预测值为 -1

总结

以上案例采用自《统计学习方法》。但是可以很明显的看到，案例中的两个特征之间有一定的影响，不是完全相互独立的。

X(1)=1X^{(1)} = 1时，X(2)X^{(2)} 是 S或者M的概率很大。 X(1)=3X^{(1)} = 3时，X(2)X^{(2)} 是 M或者L的概率很大。

要记住一点，贝叶斯模型的特点，就是基于特征之间是相互独立的。否则计算的准确定就会收到影响。所以个人觉得这并不是一个特别好的案例，大家怎么看呢？

avatar
文章
阅读
粉丝