复数域
z=x+iy或者z=x+yi,i2=−1
实数x与y分别称为复数z的实部和虚部,记作
x=Rez,y=Imz
虚部为零的复数就可以看作实数,虚部不为零的复数称为虚数
x+iy和x−iy称为互为共轭复数
复数运算
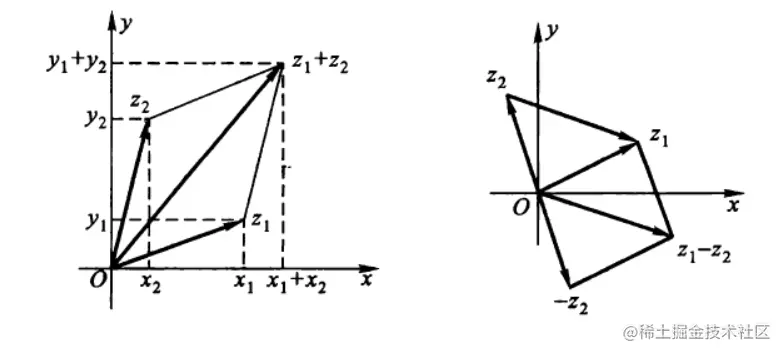
z1±z2=(x1±x2)+i(y1±y2)z1z2=(x1+iy1)(x2+iy2)=(x1x2−y1y2)+i(x1y2+x2y1)z2z1=x2+iy2x1+iy1=(x2+iy2)(x2−iy2)(x1+iy1)(x2−iy2)=x22+y22(x1x2+y1y2)+i(x2y1−x1y2),z2=0
复平面
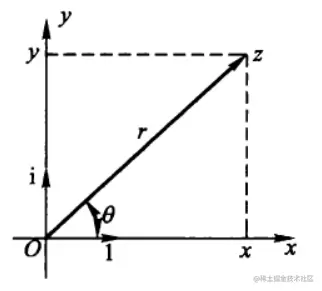
复数的模与辐角
r=∣z∣=x2+y2⩾0
tanθ=xy,称为复数z的辐角(Argument),记作θ=Argz
我们知道,任一非零复数z有无穷多个辐角,今以arg z表示其中的一个特定值,并称合条件
−π<arg z≤π
的一个为Arg z的主值,或称之为z的主辐角。
θ=Arg z=arg z+2kπ,k=0,±1,±2,⋯
当z=0时,辐角无意义。
单位复数
z=r(cosθ+isinθ)
当r=1时,有
z=cosθ+isinθ
称为单位复数。
eiθ=cosθ+isinθ (欧拉公式)
eiθ1eiθ2=ei(θ1+θ2)eiθ2eiθ1=ei(θ1−θ2)
复数的指数形式
z=reiθ
也就是说,任一非零复数z总可以表成
z=∣z∣ei arg z
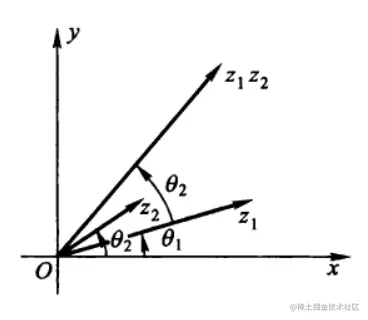
复数乘法与旋转
z1z2=r1eiθ1r2eiθ2=r1r2ei(θ1+θ2)z2z1=r2eiθ2r1eiθ1=r2r1ei(θ1−θ2)
∴∣z1z2∣=∣z1∣∣z2∣,∣z2z1∣=∣z2∣∣z1∣,z2=0
所以两个复数相乘相当于模相乘,辐角相加,相除就是模相除,辐角相减
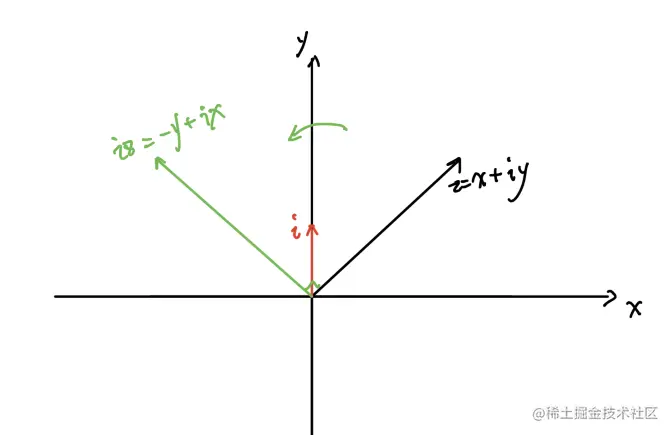
特别的我们拿i乘以一个复数
iz=i(x+iy)=−y+ix
复数的乘幂与方根
zn=(reiθ)n=rneinθ=rn(cosnθ+isinnθ),z=0∴∣zn∣=∣z∣nArg zn=nArg z
当r=1,就是棣莫弗公式
(cosθ+isinθ)n=cosnθ+isinnθ
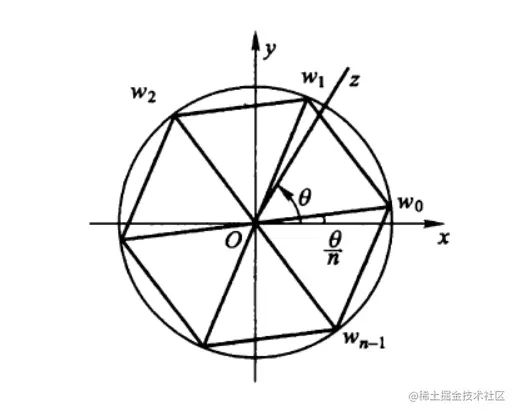
复数w的n次方就是复数z,求出复数wwn=z,z=0,n⩾2,整数
令记其根的总体为nz,设z=reiθ,w=ρeiφ,则ρneinφ=reiθ∴ρn=r,nφ=θ+2kπ
∴ρ=nr=n∣z∣φ=nθ+2kπ
所以z的n次方根为
wk=ρeiφ=nreinθ+2kπ=ein2kπ⋅nreinθ,k=0,±1,±2,⋯
把上面的式子改为
wk=ein2kπ⋅w0w0=nreinθ
wk就是在复平面内由w0依次绕原点旋转n2π,2⋅n2π,3⋅n2π,⋯
复数乘法与矩阵
假设复数p=a+bi,乘上复数q=rcosθ+irsinθpq=arcosθ−brsinθ+(arsinθ+brcosθ)i=a′+b′i用矩阵表示[a′b′]=[cosθsinθ−sinθcosθ]⋅[arbr]
这不就是二维空间中点(a,b)绕原点逆时针旋转θ角吗,模长也扩大了r倍
www.youtube.com/watch?v=lKI…