数学建模期末复习,撰写博客做总结之用,主要侧重于算例的模型建立与部分代码的实现,其中不足之处望读者多多指正。
Matlab微分求解工具箱使用
- 求数值解
dsolve(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’)
- 求解析解
[t,x]=solver(’f’,ts,x0,options)
详细的使用说明可参考博文Matlab微分方程求解
导弹问题
问题介绍
- 设位于坐标原点的甲舰向位于x轴上点A(1, 0)处的乙舰发射导弹,导弹头始终对准乙舰.如果乙舰以最大的速度(常数)沿平行于y轴的直线行驶,导弹的速度是5,求导弹运行的曲线方程.乙舰行驶多远时,导弹将它击中?
模型建立与求解
1. 解析法
模型建立:设t时刻导弹的位置为P(x(t),y(t)),乙舰位于Q(1,),由题(导弹头始终对准乙舰)可得,导弹在运动弧线p点处的切线即 又由题意(导弹速度是舰的5倍)故有: 有(1)(2)式可得微分微分方程为: 初值方程为:,,利用Matlab求解可得:
2. 数值解法
将上述方程化为一阶方程,不妨设,代入(3)中得到 利用Matlab求解:
%定义函数
function dy=eq1(x,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=1/5*sqrt(1+y(1)^2)/(1-x);
end
调用
x0=0;
xf=0.9999;
[x,y]=ode15s('eq1',[x0 xf],[0 0]);
plot(x,y(:,1),'-')
hold on
y=0:0.01:2;
plot(1,y,'*')
由图可得,导弹大致在点(1,0.2)处击中乙舰。
3. 参数方程
上述结题假设不变,在此基础再将导弹的速度设为,则在P点处有: 同时,导弹始终对准乙舰,即导弹速度向量与乙舰的位置向量平行,故有:
\frac{\mathrm{d} x}{\mathrm{d} t} \\
\frac{\mathrm{d} y}{\mathrm{d} t}
\end{array}\right)=\lambda\left(\begin{array}{l}
X-x \\
Y-y
\end{array}\right), \quad \lambda>0(2)$$
将
$$\left\{\begin{array}{l}
\frac{\mathrm{d} x}{\mathrm{d} t}=\frac{w}{\sqrt{(X-x)^{2}+(Y-y)^{2}}}(X-x) \\
\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{w}{\sqrt{(X-x)^{2}+(Y-y)^{2}}}(Y-y)
\end{array}\right.(3)$$
不妨假设乙舰速度为1,则w=5,X=1,Y=t,此时导弹的参数轨迹为:
$$\left\{\begin{array}{l}
\frac{\mathrm{d} x}{\mathrm{d} t}=\frac{5}{\sqrt{(1-x)^{2}+(t-y)^{2}}}(1-x) \\
\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{5}{\sqrt{(1-x)^{2}+(t-y)^{2}}}(t-y) \\
x(0)=0, y(0)=0
\end{array}\right.$$
matlab求解:
```php
function dy=eq2(t,y)
dy=zeros(2,1);
dy(1)=5*(1-y(1))/sqrt((1-y(1))^2+(t-y(2))^2);
dy(2)=5*(t-y(2))/sqrt((1-y(1))^2+(t-y(2))^2);
end
%调用
[t,y]=ode45('eq2',[0 2],[0 0]);
Y=0:0.01:2;
plot(1,Y,'-')
hold on
plot(y(:,1),y(:,2),'*')
```
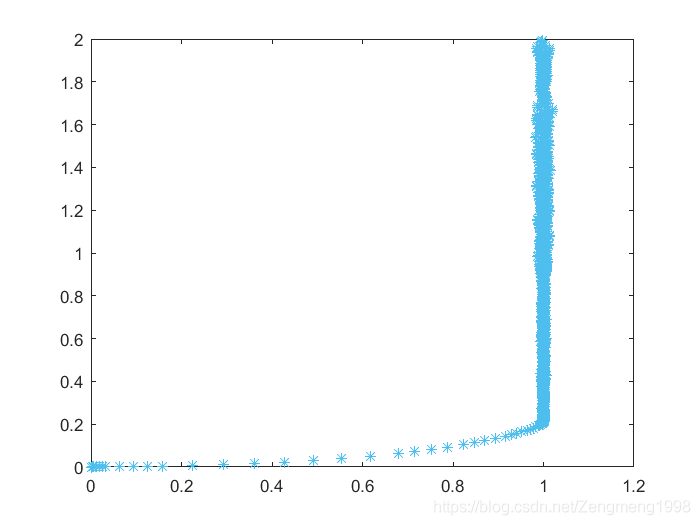
由图可得,导弹最终大致在(1,0.2)处命中目标。这里还以尝试用二分法的思想进一步得到更精确的答案,……tf=0.21是可得求解图像为:
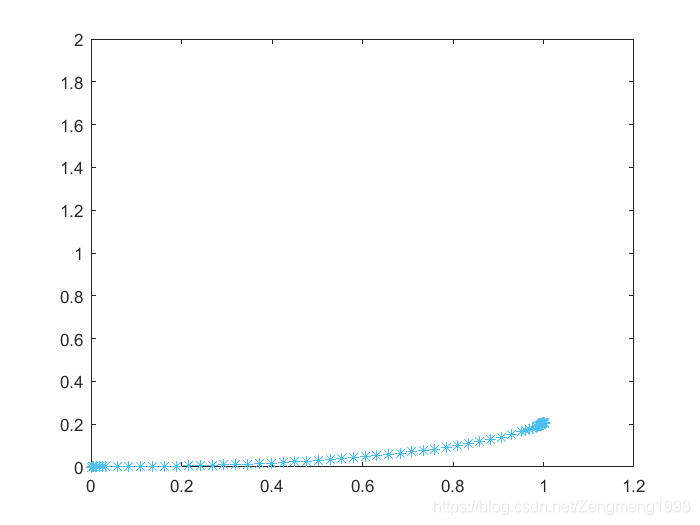
据此可得更为精确的答案。