缓解多分类的样本不均衡问题

本文首发于：行者AI

利用深度学习做多分类在工业或是在科研环境中都是常见的任务。在科研环境下，无论是NLP、CV或是TTS系列任务，数据都是丰富且干净的。而在现实的工业环境中，数据问题常常成为困扰从业者的一大难题；常见的数据问题包含有：

数据样本量少
数据缺乏标注
数据不干净，存在大量的扰动
数据的类间样本数量分布不均衡等等。

除此之外，还存在其他的问题，本文不逐一列举。针对上述第4个问题，2020年7月google发表论文《 Long-Tail Learning via Logit Adjustment 》通过 BER ( Balanced Error Rate ) 对交叉熵函数的相关推理，在原有的交叉熵的基础上进行改造，使得平均分类精度更高。本文将简要解读该论文的核心推论，并使用 keras 深度学习框架进行实现，最后通过简单的Mnist手写数字分类的实验验证结果。本文将从以下四个方面进行解读：

基本概念
核心推论
代码实现
实验结果

1. 基本概念

基于深度学习的多分类问题中，想要获得更优的分类效果往往需要对数据、神经网络的结构参数、损失函数以及训练参数做出调整；尤其是在面对类别不均衡的数据时，做出的调整更多。在论文《 Long-Tail Learning via Logit Adjustment 》中，为了缓解类别不均衡造成的低样本类别分类准确率低的问题，只向损失函数中加入了标签的先验知识便获得了SOTA效果。因此，本文针对其核心推论，首先简要阐述四个基本概念：（1）长尾分布、（2）softmax、（3）交叉熵、（4）BER

1.1 长尾分布

如果将所有类别的训练数据按照每类的样本量进行从高到低的排序，并将排序结果表现在图形上，那么类别不均衡的训练数据将会呈现出 “头部” 和 “尾部” 的分布形式，如下图所示：

样本量多的类别形成 “头部” ，样本量低的类别形成 “尾部” ，类别不均衡问题很显著。

1.2 softmax

softmax 由于其归一化的功能以及易于求导的特点，常在二分类或多分类问题中作为神经网络最后一层的激活函数，用于表达神经网络的预测输出。本文对softmax 不多做赘述，只给出其一般化的公式：

$q\left(c_{j}\right)=\frac{e^{z_{j}}}{\sum_{i=1}^{n} e^{z_{i}}}$

在神经网络中， $z_{j}$ 是上一层的输出； $q\left(c_{j}\right)$ 是本层输出的分布形式； $\sum_{i=1}^{n} e^{z_{i}}$ 是一个 batch内 $e^{z_{i}}$ 的和。

1.3 交叉熵

本文对交叉熵函数不做过多推论，详情可查阅信息论的相关文献。二分类或多分类问题中，通常以交叉熵函数及其变体作为损失函数进行优化，给出基本公式：

$H(p, q)=-\sum_{i} p\left(c_{i}\right) \log q\left(c_{i}\right)$

在神经网络中， $p\left(c_{i}\right)$ 是期望的样本分布，通常是one-hot编码后的标签； $q\left(c_{i}\right)$ 是神经网络的输出，可视作神经网络对样本的预测结果。

1.4 BER

BER 在二分类中为正例样本和负例样本中各自预测错误率的均值；在多分类问题中为各类样本各自错误率的加权和，可以表示为以下形式（参照论文）：

$\operatorname{BER}(f) \doteq \frac{1}{L} \sum_{y \in[L]} \mathbb{P}_{x \mid y}\left(y \notin \operatorname{argmax}_{y^{\prime} \in y} f_{y^{\prime}}(x)\right)$

其中， $f$ 是整个神经网络； $f_{y^{\prime}}(x)$ 表示输入为 $x$ ，输出为 $y^{\prime}$ 的神经网络； $y \notin \operatorname{argmax}_{y^{\prime} \in y} f_{y^{\prime}}(x)$ 表示被神经网络错误识别的标签 $y$ ； $\mathbb{P}_{x \mid y}$ 即为错误率的计算形式； $\frac{1}{L}$ 为各类权重。

2. 核心推论

按照论文思路，首先确定一个神经网络模型：

$f^{*} \in \operatorname{argmin}_{f:} x \rightarrow \mathbb{R}^{L} \text { BER }(f)$

即 $f^{*}$ 为满足BER条件的一个神经网络模型。接着优化这一神经网络模型 $\operatorname{argmax}_{y \in[L]} f_{y}^{*}(x)$ ，这一过程等价于 $\operatorname{argmax}_{y \in[L]} \mathbb{P}^{\mathrm{bal}}(y \mid x)$ ，即给定训练数据 $x$ 得到预测标签 $y$ ，并将预测标签 $y$ 均衡化（乘上各自权重）的优化过程。简写为：

$\operatorname{argmax}_{y \in[L]} f_{y}^{*}(x)=\operatorname{argmax}_{y \in[L]} \mathbb{P}^{\mathrm{bal}}(y \mid x)=\operatorname{argmax}_{y \in[L]} \mathbb{P}(x \mid y)$

对于 $\mathbb{P}^{\text {bal }}(y \mid x)$ ，显然 $\mathbb{P}^{\text {bal }}(y \mid x) \propto \mathbb{P}(y \mid x) / \mathbb{P}(y)$ ，其中 $\mathbb{P}(y)$ 是标签先验； $\mathbb{P}(y \mid x)$ 是给定训练数据 $x$ 之后的预测标签的条件概率。结合多分类神经网络中训练的实质：

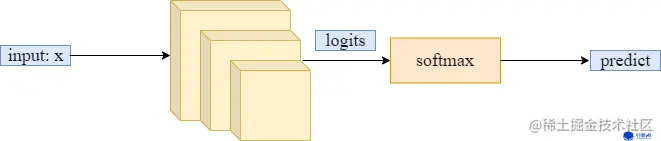
依照上述过程，假设将网络输出logits记为s*： $s^{*}: x \rightarrow \mathbb{R}^{L}$ ，由于 $s^{*}$ 需要通过 softmax 激活层，即 $q\left(c_{i}\right)=\frac{e^{s^{*}}}{\sum_{i=1}^{n} e^{s^{*}}}$ ；因此不难得出： $\mathbb{P}(y \mid x) \propto \exp \left(s_{y}^{*}(x)\right)$ 。再结合 $\mathbb{P}^{\text {bal }}(y \mid x) \propto \mathbb{P}(y \mid x) / \mathbb{P}(y)$ ，可以将 $\mathbb{P}^{\text {bal }}(y \mid x)$ 表示为：

$\operatorname{argmax}_{y \in[L]} \mathbb{P}^{\text {bal }}(y \mid x)=\operatorname{argmax}_{y \in[L]} \exp \left(s_{y}^{*}(x)\right) / \mathbb{P}(y)=\operatorname{argmax}_{y \in[L]} s_{y}^{*}(x)-\ln \mathbb{P}(y)$

参照上式，论文中给出了优化 $\mathbb{P}^{\text {bal }}(y \mid x)$ 的两种实现方式：

（1）通过 $\operatorname{argmax}_{y \in[L]} \exp \left(s_{y}^{*}(x)\right) / \mathbb{P}(y)$ ，在输入 $x$ 通过所有神经网络层得到预测predict后，除以一个先验 $\mathbb{P}(y)$ 。这种方法前人已经用过了，并且取得了一定的效果。

（2）通过 $\operatorname{argmax}_{y \in[L]} s_{y}^{*}(x)-\ln \mathbb{P}(y)$ ，在输入 $x$ 通过神经网络层得到一个编码logits后减去一个 $\ln \mathbb{P}(y)$ 。论文采用的是这一种思路。

依照第二条思路，论文直接给出了一个一般化的式子，称之为logit adjustment loss：

$\ell(y, f(x))=-\log \frac{e^{f_{y}(x)+\tau \cdot \log \pi_{y}}}{\sum_{y^{\prime} \in[L]} e^{f_{y^{\prime}}(x)+\tau \cdot \log \pi_{y^{\prime}}}}=\log \left[1+\sum_{y^{\prime} \neq y}\left(\frac{\pi_{y^{\prime}}}{\pi_{y}}\right)^{\tau} \cdot e^{\left(f_{y^{\prime}}(x)-f_{y}(x)\right)}\right]$

对比常规的softmax交叉熵：

$\ell(y, f(x))=\log \left[\sum_{y^{\prime} \in[L]} e^{f_{y^{\prime}}(x)}\right]-f_{y}(x)=\log \left[1+\sum_{y^{\prime} \neq y} e^{f_{y^{\prime}}(x)-f_{y}(x)}\right]$

本质上是将一个与标签先验有关的偏移量应用到了每一个对数输出中（即经过softmax激活之前的结果）。

3. 代码实现

实现的思想在于：对神经网络的输出logits加上一个基于先验的偏移 $\log \left(\frac{\pi_{y^{\prime}}}{\pi_{y}}\right)^{\tau}$ 。在实际中，为了在尽量有效的前提下简便实现，取调节因子 $\tau$ =1， $\pi_{y^{\prime}}$ =1。则logit adjustment loss简化为：

$\ell(y, f(x))=-\log \frac{e^{f_{y}(x)+\tau \cdot \log \pi_{y}}}{\sum_{y^{\prime} \in[L]} e^{f_{y^{\prime}}(x)+\tau \cdot \log \pi_{y^{\prime}}}}=\log \left[1+\sum_{y^{\prime} \neq y} e^{\left(f_{y^{\prime}}(x)-f_{y}(x)-\log \pi_{y}\right)}\right]$

在keras框架下实现如下：

import keras.backend as K

def CE_with_prior(one_hot_label, logits, prior, tau=1.0):
    '''
    param: one_hot_label
    param: logits
    param: prior: real data distribution obtained by statistics
    param: tau: regulator, default is 1
    return: loss
    '''   
    log_prior = K.constant(np.log(prior + 1e-8))

    # align dim 
    for _ in range(K.ndim(logits) - 1):     
        log_prior = K.expand_dims(log_prior, 0)

    logits = logits + tau * log_prior
    loss = K.categorical_crossentropy(one_hot_label, logits, from_logits=True)

    return loss

4. 实验结果

论文《 Long-Tail Learning via Logit Adjustment 》本身对比了多种提升长尾分布分类精度方法，并使用了不同的数据集进行测试，测试表现优于现有的方法，详细的实验结果参照论文本身。本文为了快速验证实现的正确性，以及该方法的有效性，使用mnist手写数字进行了简单的分类实验。实验背景如下：

\	详情
训练样本	0 ~ 4：5000张/类；5 ~ 9 :500张/类
测试样本	0 ~ 9：500/类
运行环境	本地CPU
网络结构	卷积+最大池化+全连接

在上述背景下进行对比实验，对比标准的多分类交叉熵和带先验的交叉熵分别作为loss函数下，分类网络的表现。取相同的epoch=60，实验结果如下：

\	标准多分类交叉熵	带先验的交叉熵
准确率	0.9578	0.9720
训练流程图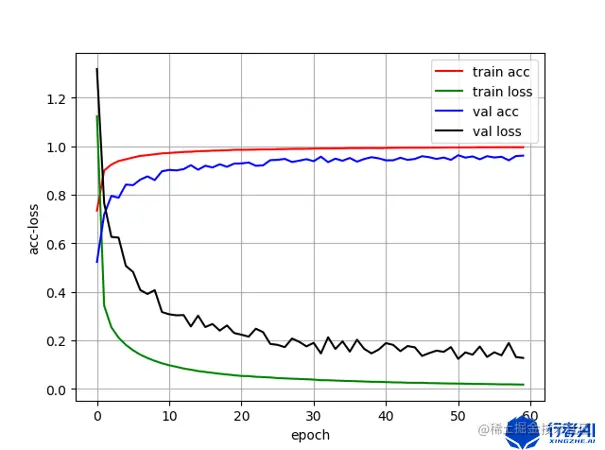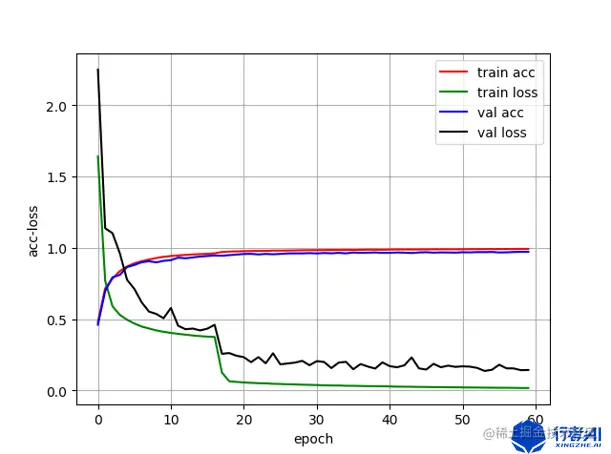

PS：更多技术干货，快关注【公众号 | xingzhe_ai】，与行者一起讨论吧！