笔记内容全部基于西安电子科技大学 鱼亮 老师的 《离散数学II》课堂内容整理
博主数学水平相当一般,内容从数学的角度来看可能相当不严谨甚至存在谬误,仅供参考。
欢迎高人指点
这里简单列一下群的主要性质等,方便阅读本文时查阅:
群,是运算可结合、存在幺元、每个元素都有逆元的代数系统;每个元素都能用其他元素表示;运算满足消去律;幺元是唯一的等幂元
循环群,其中每个元素都可以用生成元的幂次表示;循环群是阿贝尔群(运算可交换)
子群的含义
子群的载体是原群载体的子集,运算仍然封闭,每个元素都有逆元,且原群的幺元在子群中仍然存在。(子群的运算默认是可结合的,因为原群是群,群的运算必须可结合,且运算的结合律是可继承的)
平凡子群:平凡子群包括原群本身,以及载体只含一个幺元的子群(注意:群中没有零元,只有幺元,幺元是群中唯一的等幂元),例如:
群 <G,∗> 的平凡子群是 <G,∗> 和 <{e},∗>
若题目需要求一个群的子群,可以先写上两个平凡子群,然后再写一般的非平凡子群。
例:已知 <I,+> 是一个群,设集合 IE={x∣x=2n,n∈I} ,问 <IE,+> 是 <I,+> 的子群吗?

子群判定定理
定理1
已知群 <G,∗>,已知 S 是 G 的非空子集,运算 ∗ 在 S 上封闭,S 的每个元素都有逆元。则 <S,∗> 是 <G,∗> 的子群

定理2
若 <G,∗> 是群,S⊆G , S=∅ 且 S 是有限集,则只要 ∗ 在 S 上封闭,则可确定 <S,∗> 是 <G,∗> 的子群
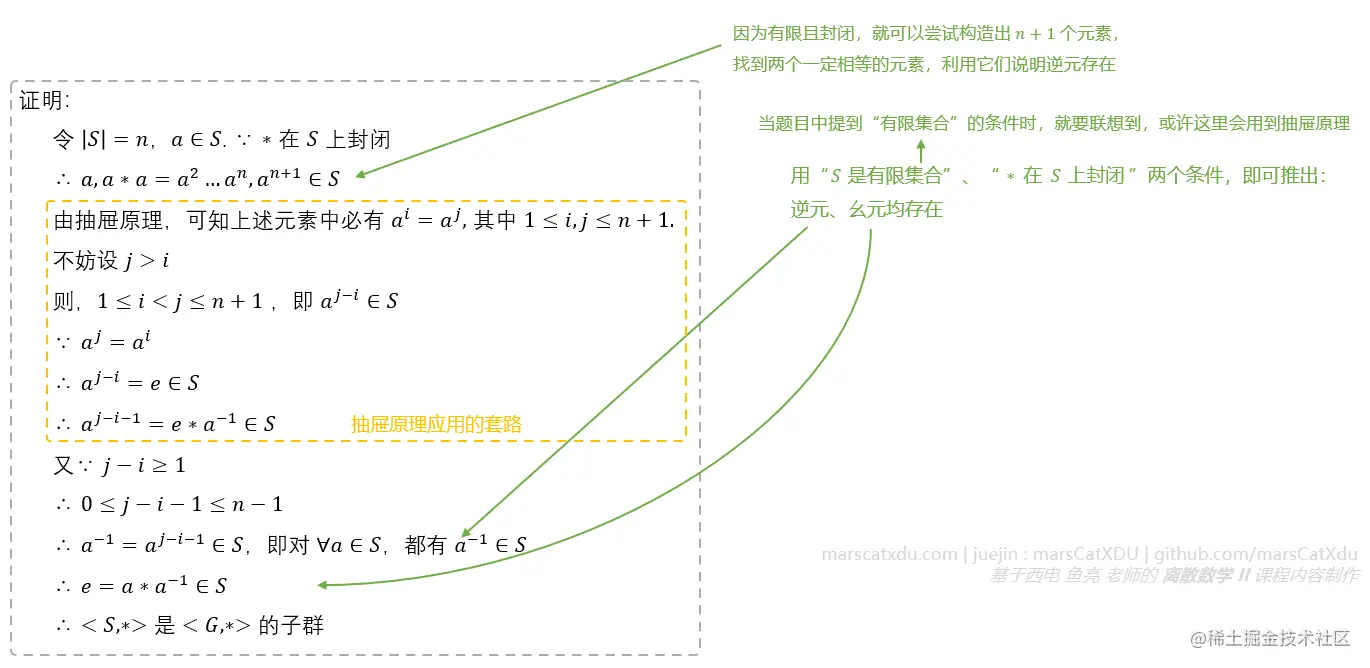
例:
求 <N6,+6> 的所有子群

定理3
设 <G,∗> 是一个群,S⊆G,S=∅, 对 ∀a,b∈S,若有 a∗b−1∈S,则 S 是 G 的子群


例题和其他定理
例1
设 <H,∗> 、<K,∗> 均为 <G,∗> 的子群,请证明:<H∩K,∗> 是 <G,∗> 的子群

例2
已知 <G,∗> 是群,取 ∀a∈G,令 H={x∣x∗a=a∗x,x∈G},试证明:<H,∗> 是 <G,∗> 的子群

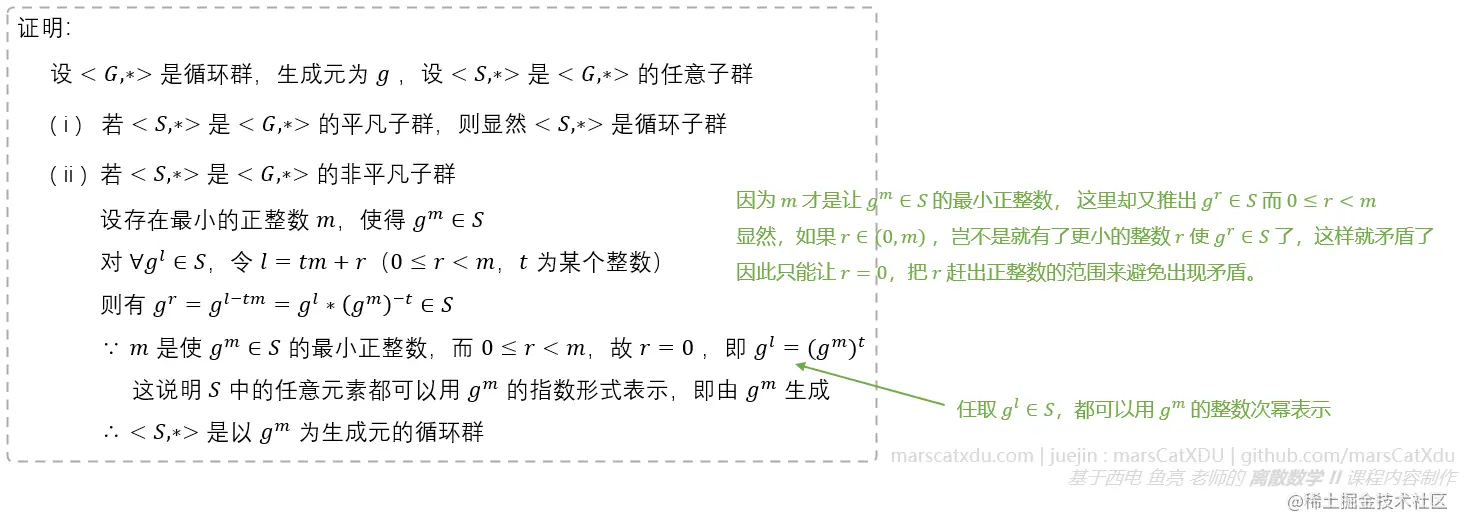
定理:循环群的子群必为循环群
回顾:循环群中的每个元素都可用生成元的幂次表示
想要确定循环群的子群是否为循环群,实际上就是要看能否找到该子群的生成元。由于该子群未必有限,因此未必能够找到最大的指数,但肯定能找到最小的。
群同态
设两个群 <G,⋅>、<H,⊙> ,有映射 h:G→H, 对 ∀a,b∈G,有 h(a⋅b)=h(a)⊙h(b) 。则称 h 是从 <G,⋅> 到 <H,⊙> 的群同态。 <h(G),⊙> 是 <G,⋅> 的同态象。
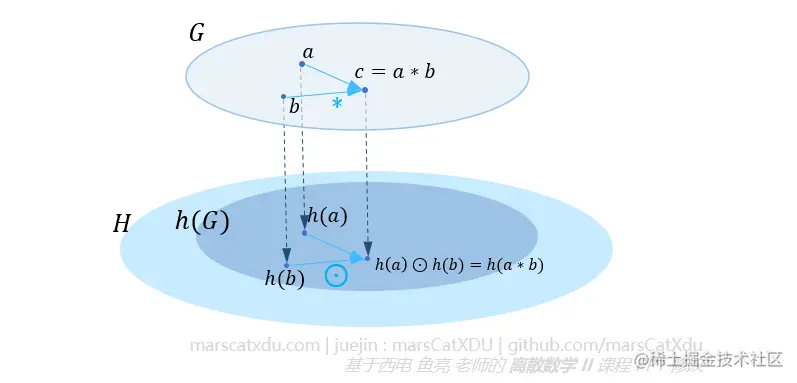
性质
定理:设 h 是从群 <G,∗> 到群 <H,⊙> 的一个同态映射,则 <G,∗> 在 h 下的同态象 <h(G),⊙> 也是群。

定理:设 h 是从群 <G,∗> 到群 <H,⊙> 的一个同态映射,则 <G,∗> 在 h 下的同态象 <h(G),⊙> 是 <H,⊙> 的子群【证明略,由于上一个定理的存在,这里只需证明载体的子集关系即可】
同态核
设 h 是从群 <G,∗> 到群 <H,★> 的一个同态映射, eH 是 <H,★> 的幺元。则 Ker(h)={x∣x∈G∧h(x)=eH} 被称为【群同态映射 h 的核】,简称【 h 的同态核 】。
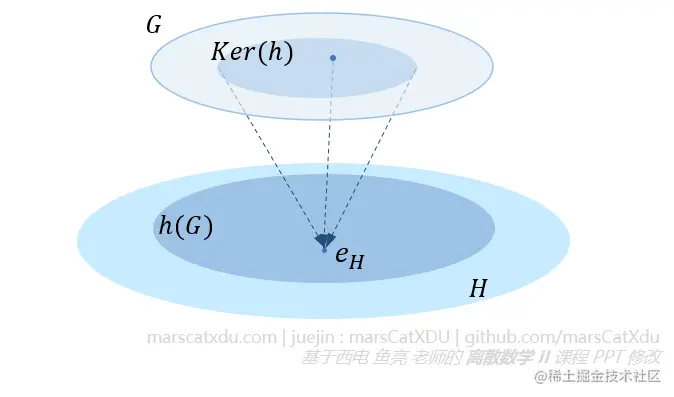
Ker(h) 是 G 的子集,其中的元素进行映射 h 都会指向幺元 eH (因为并没有要求 h 的映射方式,所以这里的映射可以出现多对一的情况,也就是说同态核的元素多于一个)
同态核的性质
定理:设 h 是从群 <G,∗> 到 <H,★> 的一个同态映射,Ker(h) 是 h 的同态核,则 <Ker(h),∗> 是 <G,∗> 的子群
解析:要判断子群关系,可以使用上面的判定定理。这里采用判定定理1

定理:设 <G,∗> 是以 g∈G 为生成元的循环群
(a) 若 G 是无限集,则 <G,∗> 与 <I,+> 同构;
(b) 若 G 是有限集,且 ∣G∣=k,则 <G,∗> 与 <Nk,+k> 同构
