• 原文地址：Diverse Mini-Batch Active Learning: A Reproduction Exercise
• 原文作者：Alexandre Abraham
• 译文出自：掘金翻译计划
• 本文永久链接：github.com/xitu/gold-m…
• 译者：z0gSh1u
• 校对者：Aurevior

重现：多样化 Mini-Batch 主动学习

在我们先前的博文 主动学习工具包一瞥 中，我们为最基础的主动学习方法、相关的常用 Python 库，以及它们实现的更高级的方法，给出了一个概览。

在本篇中，我们将介绍一些最新的方法，并借此机会重现 2019 年的论文 Diverse Mini-Batch Active Learning 的结果。读者可以直接前往该文章进行阅读，以便完整详细的了解所有的方法。

多样化的重要性

在之前的文章中，介绍了一种基于不确定度的方法，这种方法使用“类别预测概率”来选择最为复杂、纠结的样本。另外还有一种基于密度的方法，这种方法是利用数据的分布来选择最具代表性的样本。

不确定性和代表性是主动学习希望能够优化的三样评价准则中的两个：

• 多样性。 多样性是纯粹探索性的准则。一个单纯优化多样性的方法很可能会选遍整个特征空间的样本，并且更倾向于选择离群的样本。
• 代表性。 如果许多其他样本与该样本在某一个给定的相似度度量标准下是相似的，那么这个样本就称作“有代表性的”。典型的代表性样本是大的样本聚类的“中心“。
• 不确定性。 也就是模型难以分类的那些样本。

多样性和代表性通常同时被优化，因为二者都利用无标签数据的分布。聚类方法能一次优化二者。这就是作者为什么为他的多样性查询取样方法选择 K-均值聚类。另一个策略是例如 [1] 提出的一个基于相似性矩阵的方法，它在一个损失函数中集合了所有的评价准则。

多样性对于补偿基于不确定度方法的探索是很有必要的，它主要关注靠近决策边界的区域。

图1. 在这个小例子中，带颜色的样本是已被打标签的，当前分类器边界显示为紫色。基于不确定度的方法更倾向于选择在红色区域的、更靠近分类器边界的样本。基于代表性的方法更倾向于选择在紫色区域的样本，因为样本的密度更高。只有基于多样性的方法倾向于探索蓝色区域。

图1 展示了一个简单的在二元分类（方形、三角形）上的主动学习实验。它表明基于不确定性或者代表性的方法会错过特征空间的整块区域，进而无法构建一个在未见数据上泛化能力好的模型。

综上所述，使用聚类方法可以比较自然的分隔空间。聚类应当有相似样本构成，聚类方法既可以区分不同的特征，又可以找到每个聚类中的代表性样本。

多样化 Mini-Batch 主动学习策略

多样化 Mini-Batch 主动学习方法通过选择接下来 k 个要打标签的样本，结合了不确定性和多样性：

• 首先，使用最小边缘取样器 [2] 预选 β * k 个样本，β 是该方法的唯一参数。
• 然后从预选样本中选择 k 个，可以使用 次模函数优化器 Submodular(β)、K-均值 聚类 Clustered(β)，或是不确定性加权的 K-均值 聚类 WClustered(β)。这篇论文的实验参数是 β=10 和 β=50。

注： 论文提到，解多样性问题最好的方法是次模函数优化，K-均值 聚类只是该问题的一个参考。这个主题对于一篇简单的博文来说太复杂了，所以我们为好奇的读者给出原论文以及 维基百科页面 ！

我们决定比较使用 apricot Python 库 中的次模函数优化器和 scikit-learn 中的 K-均值 聚类优化器。

为什么选这篇论文？

在主动学习领域，我们有大量的文章可以选择。我们基于如下几个准则来选择文章：

充分的验证。 我们注意到，大量主动学习的论文只是在 OpenML 的小数据集上测试了它们的方法，而没有在主动学习场景下应有的充足样本 —— 通常，这些论文只是用 150 个样本，就说达到 0.95 的准确率。因此，我们想要在更大的数据集上复现论文，而这篇文章，使用了 20 Newsgroups、MNIST 和 CIFAR10 数据集，看起来足够复杂，又不需要大量的资源就可以复现。

简单而优雅的方法。 大多数近期的论文，关注的是主动学习领域特定的深度模型；其中一些甚至是与模型结构相关的。我们希望有一个足够简单，从而可理解、可复现的方法。这篇论文提出的方法基于 K-均值 聚类 —— 一个原理符合直觉的、广泛使用的聚类算法。

既优化不确定性，也优化多样性。 大多数现代的主动学习方法优化模型的不确定性和特征的探索 —— 也就是多样性。论文提出的方法用不确定性作为样本预选和 K-均值 聚类的样本权重，很自然地结合了这些指标。

注： 在这篇论文中，作者将他的方法与一个叫 FASS 的框架进行比较。出于简单性的考虑，我们在这篇博文中没有复现这个框架的结果。我们也决定使用 Keras 而不是惯用的 MXNet，来看看用另一个框架能不能做到实验结果的重现。

勘误：不确定度计算

在这篇论文中，作者通过最大化下面这个式子，来定义信息量：

其中 ŷ₁ 是首个标签、ŷ₂ 是次个，正如 [2] 推荐的，应最小化它。我们通过实验确认了这一点，最大化它带来的性能还不如随机采样。我们猜想作者应该是使用了通常的互补概率处理：

20 Newsgroups 数据集实验

20 Newsgroups 的任务是区分一系列文章来自 20 个讨论组中的哪一个。对于这个实验，我们使用了与论文描述完全一致的配置：

• 预处理是使用 CountVectorizer(ngram_range=(1,2), max_features=250000) 和 TfidfTransformer(use_idf=True) —— 等效于 TfidfVectorizer(ngram_range=(1,2), max_features=250000, use_idf=True, dtype=np.int64) —— 分类器是使用多项式 Logistic 回归。
• 我们从 100 个样本开始，在第 100 个 batch 调整到 1,000 个样本。
• 一点不同：对于数据的高维度性，我们使用 MiniBatchKMeans 作为 Clustered(50) 和 WClustered(50) 来加快实验速度。

结论： 在这个实验中，我们没能复现原文的结果，但也没有产生与原文冲突的结果。特别地，随机采样似乎在原实验中在 1,000 个样本上达到了 0.68 的准确率，其他的方法大概在 0.70 左右。最后，由于结果的变异性很强，我们不能断言某个方法就比另一个要好。

MNIST 数据集实验

这篇文章提出了两种在 MNIST 数据集上的实验，我们在此复现了第一个。这是一个在 MNIST 上的数字识别的主动学习实验。主动学习循环从 100 个样本开始，逐步增加 100 个样本，直到 1,000 个样本（总数为 60,000），最好的准确率是 0.93。这篇论文给出了一个模型设定的 Python notebook，但我们用相同的设定没能复现一样的结果：

• 我们使用 Keras 而不是 MXNet 来搭建神经网络，但结构是相同的 —— 大小为 128、64 的层，ReLU 激活函数，最后是使用 softmax 的 10 个神经元的层。
• 我们没能用文章给定的设置复现高于 0.90 的准确率 —— 学习率为 0.10 的 SGD 优化器。我们换用学习率为 0.01 的 Adam 获得了类似的性能。
• 我们使用 60,000 个样本作训练集，10,000 个作测试集，与论文中提到的一样。但运行 20 次实验而不是 16 次。

本实验最令人惊奇的结果是我们的置信区间显著地大于原论文的结果，尽管我们使用的是相同的置信区间计算方式，并且重复了多于 16 次实验。

同时，我们观察到随机法要显著地差于所有的主动学习方法。纯粹基于不确定度的方法在某些地方比基于聚类的方法要差一点，但也不是太多。同时，由于它更容易搭建，可能仍然是一个值得考虑的选择。最后，原文的图形表明聚类的方法在 400 个样本左右时只有细微的差别。我们没能复现这种差别，也没有观测到这些样本有相似的表现。

在这三个实验中，我们尤其关注这些结果，因为 MNIST 是不同采样方法之间区别最明显的实验。我们的实验与原版的最大不同是模型的实现，我们决定使用另一个东西来复现实验：scikit-learn 的多层感知机。我们也想确认我们选择的不确定性度量：最小边缘，会像论文说的一样表现的比最低置信度的度量要好。结果如下：

图4 展示的结果与原文的接近得多。最小边缘采样的表现显著地好于最小置信度采样。当学习的数据集样本量在 300 到 800 之间时，加权的聚类方法显著地好于其他的方法。置信区间也小得多，尽管没有论文中那样窄。图中一个令人激动的发现是，加权的聚类方法似乎表现得一致地独立于基于信息量的样本预选和加权方法。

结论： 尽管有一些微小的不同，这两组实现都可以证实原文的观点。我们发现，基于多样性的方法比基于不确定度的方法更有效。有趣的是，这两种方法都要比基于信息量的方法要更有效。

CIFAR 10 数据集实验

这是一个在 CIFAR 10 数据集上的图像分类实验。由于运行这个任务需要更广的训练集，主动学习从 1,000 个样本开始，然后逐步增加 1,000 个样本，直到 10,000 个（总数 50,000），达到了大约 0.60 的准确率。我们对这个实验的配置是：

• 我们使用 Keras 而不是 MXNet，使用Resnet 50 v2 而不是 Resnet 34 v2，因为它不是 Keras 原生提供的。因为论文没有指定优化器，我们使用 RMSprop 运行了 3 个 epoch。
• 我们使用了 50,000 个训练样本和 10,000 个测试样本，与论文一致。

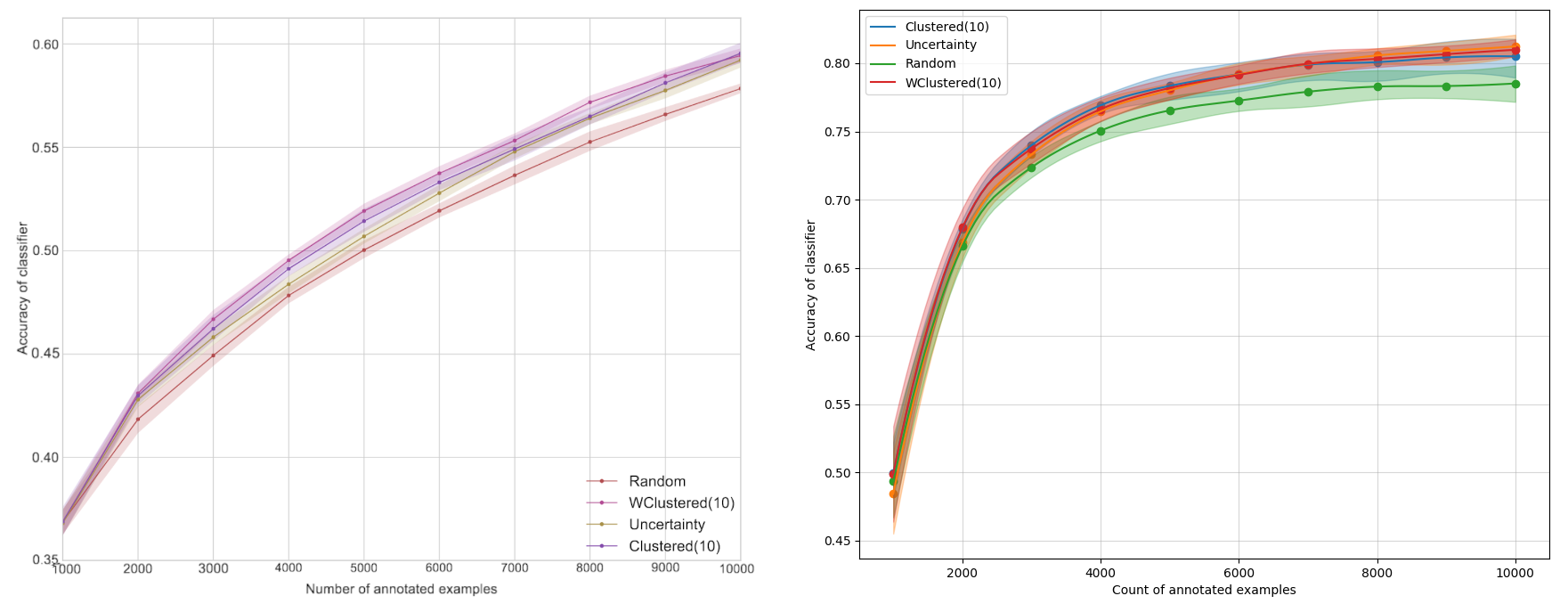
结论： 图5 表明我们的置信区间又一次比原文的稍大一些。最惊人的结果是我们的准确率比原文要高得多 —— 0.8 而不是 0.6。这个不同应该是两个实验的架构不同导致的。然而，再一次地，我们观察到主动学习比随机采样要好，虽然我们没有观察基于多样性的采样方法有更好的性能。

多样化 Mini-batch 主动学习：总结

复现一篇研究文章的实验总是复杂的，尤其是在原实验的参数没有完全公开分享的情况下。

我们无法解释的一件事是，与原文比起来，我们的实验结果的变异性更高。即使我们使用了稍有不同的技术和设置，我们仍成功复现了论文的主要发现，证明了主动学习在复杂问题上也确实有用。

引用

Zhdanov, Fedor. “Diverse mini-batch Active Learning.” arXiv preprint arXiv:1901.05954 (2019).

[1] Du, Bo, et al. “Exploring representativeness and informativeness for active learning.” IEEE transactions on cybernetics 47.1 (2015): 14–26.

[2] Settles, Burr. Active learning literature survey. University of Wisconsin-Madison Department of Computer Sciences, 2009.

如果发现译文存在错误或其他需要改进的地方，欢迎到 掘金翻译计划 对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

掘金翻译计划 是一个翻译优质互联网技术文章的社区，文章来源为 掘金 上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注 掘金翻译计划、官方微博、知乎专栏。