目录
语音降噪是语音信号处理的初始步骤,目前已经有很多成熟的算法。而谱减法作为经典的降噪算法实现简单,运行处理快,被广泛的应用在语音降噪领域。
1. 谱减法原理
谱减法顾名思义,就是用带噪信号的频谱减去噪声信号的频谱(幅度谱和功率谱均可)。谱减法基于一个简单的假设:假设语音中的噪声只有加性噪声,只要将带噪语音谱减去噪声谱,就可以得到纯净语音,这么做的前提是噪声信号是平稳的或者缓慢变化的。提出这个假设就是基于短时谱(25ms),就是频谱在短时间内是平稳不变的。假设带噪信号y由纯净信号x和加性噪声d组成,那么纯净信号的功率谱可以通过下式获得:
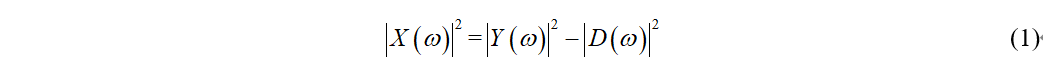
谱减法的实现的关键在于对噪声谱的估计,一般认为语音信号的前几帧没有语音活动,因此前几帧为纯净的噪声信号,因此使用语音信号的前几帧对噪声谱进行估计。
2. 谱减法的实现
简单的谱减法实现包含以下步骤:
-
根据语音信号前几帧计算平均噪声谱作为噪声谱,一般取前5帧
-
对语音进行分帧,对每一帧进行stft,然后使用信号谱减去噪声谱
-
如果出现负值,将其置为0
-
对减去噪声谱的信号进行istft得到时域信号
-
根据语音分帧帧长和帧移长度重组时域信号
在谱减法算法中如果带噪语音的幅度谱(功率谱也同此理)与估计出来的噪声谱相减出现负值时,说明对噪声出现了过估计问题,对这种现象最简单的处理就是将负值设为0,以保证非负的幅度谱。但是对负值的这种处理,会导致信号帧频谱的随机位置上出现小的,独立的峰值,称为音乐噪声。为解决音乐噪声Berouti提出了改进的方法。
3. Berouti谱减法的实现
减小音乐噪声的方法是对噪声谱使用过减技术,同时对谱减后的负值设置一个下限,而不是将它们设为0,可以将其表示为:
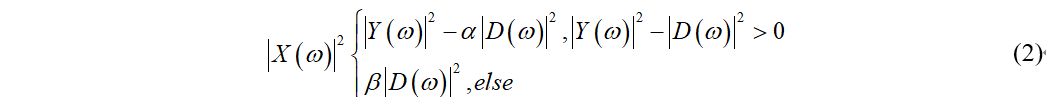
其中alpha(大于等于1)为过减因子,它主要影响语音谱的失真程度。Beta(大于0小于1)是谱下限参数,可以控制残留噪声的多少以及音乐噪声的大小。在谱减法过程中,beta为一个固定值,而alpha根据当前帧的信噪比进行计算。Berouti谱减法包含以下步骤:
-
根据语音信号前几帧计算平均噪声谱作为噪声谱,一般取前5帧
-
对语音进行分帧,对每一帧进行stft
-
计算当前帧的信噪比,然后求出过减因子alpha
-
根据公式(2)对信号进行处理
-
对减去噪声谱的信号进行istft得到时域信号
-
根据语音分帧帧长和帧移长度重组时域信号
最后我们看下谱减法的效果,如下图所示。可以看出Berouti提出了改进的方法要优于原始的谱减法。
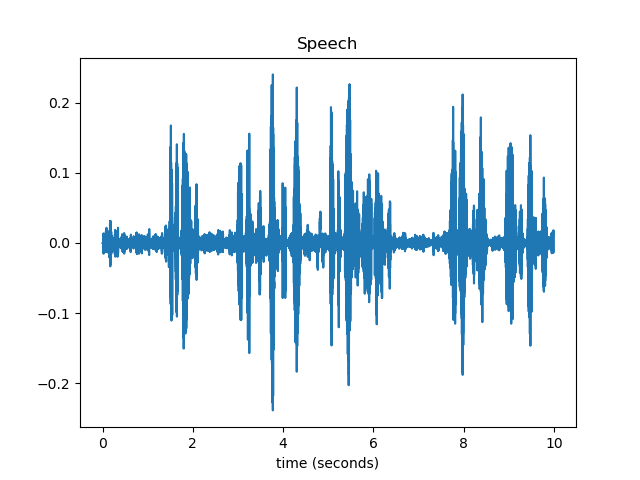
原始语音波形:
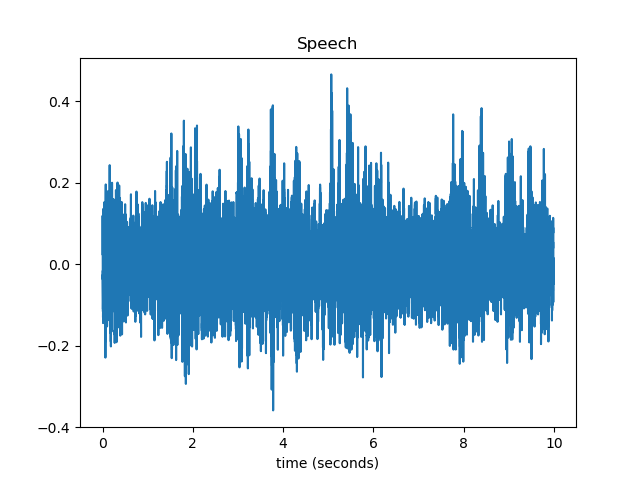
原始谱减法后波形:
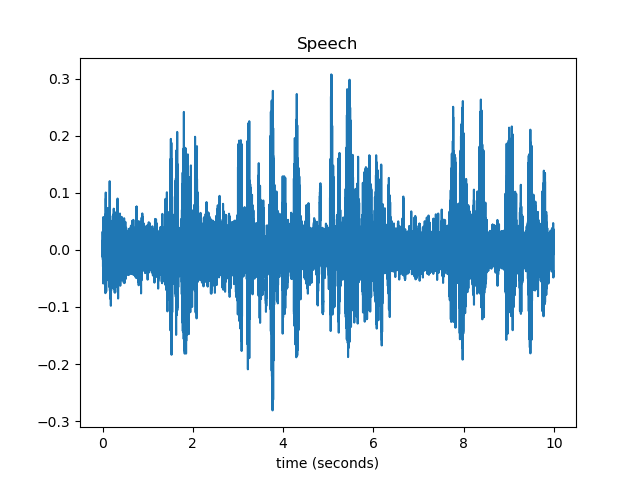
Berouti谱减法处理后信号波形:
关注微信公众号语音算法组,在公众号菜单栏点击More->Code即可获得代码