4.1 简介
本次任务将学习一种在深度学习之前非常流行的图像特征提取技术——方向梯度直方图（Histogram of Oriented Gradients），简称HOG特征。HOG特征是在2005年CVPR的会议发表，在图像手工特征提取方面具有里程碑式的意义，当时在行人检测领域获得了极大成功。
学习HOG特征的思想也有助于我们很好地了解传统图像特征描述和图像识别方法，本次任务我们将学习到HOG背后的设计原理，和opencv的实现。
4.2 内容介绍
1. HOG特征简介
HOG特征是一种图像局部特征，其基本思路是对图像局部的梯度幅值和方向进行投票统计，形成基于梯度特性的直方图，然后将局部特征拼接起来作为总特征。局部特征在这里指的是将图像划分为多个子块（Block), 每个Block内的特征进行联合以形成最终的特征。
HOG+SVM的工作流程如下：
首先对输入的图片进行预处理，然后计算像素点的梯度特特性，包括梯度幅值和梯度方向。然后投票统计形成梯度直方图，然后对blocks进行normalize，最后收集到HOG feature（其实是一行多维的vector）放到SVM里进行监督学习，从而实现行人的检测。下面我们将对上述HOG的主要步骤进行学习。
2.HOG特征的原理
图像预处理
预处理包括灰度化和Gamma变换。
灰度处理是可选操作，因为灰度图像和彩色图像都可以用于计算梯度图。对于彩色图像，先对三通道颜色值分别计算梯度，然后取梯度值最大的那个作为该像素的梯度。
然后进行伽马矫正，调节图像对比度，减少光照对图像的影响（包括光照不均和局部阴影），使过曝或者欠曝的图像恢复正常，更接近人眼看到的图像。
- 伽马矫正公式：
，表示图像，表示幂指数。
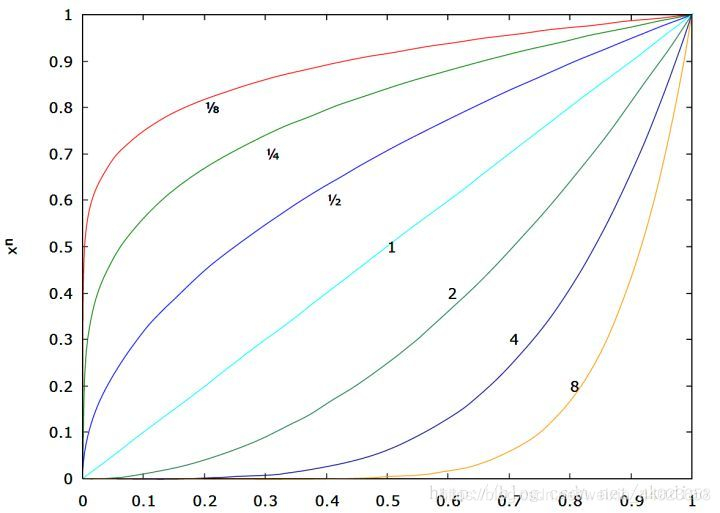
如图，当取不同的值时对应的输入输出曲线( 时输入输出保持一致) ： 1） 当时，输入图像的低灰度值区域动态范围变大，进而图像低灰度值区域对比度得以增强；在高灰度值区域，动态范围变小，进而图像高灰度值区域对比度得以降低。 最终，图像整体的灰度变亮。
2） 当时，输入图像的低灰度值区域动态范围变小，进而图像低灰度值区域对比度得以降低；在高灰度值区域，动态范围变大，进而图像高灰度值区域对比度得以增强。 最终，图像整体的灰度变暗。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('E:/python-project/deep-learning/picture/test1.jpg', 0)
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
img2 = np.power(img/float(np.max(img)),1/2.2)
plt.imshow(img2)
plt.axis('off')
plt.show()
计算图像梯度
为了得到梯度直方图，那么首先需要计算图像水平方向和垂直方向梯度。 一般使用特定的卷积核对图像滤波实现，可选用的卷积模板有：soble算子、Prewitt算子、Roberts模板等等。
一般采用soble算子，OpenCV也是如此，利用soble水平和垂直算子与输入图像卷积计算、：
\text {Sobel}_{X}=\left[\begin{array}{c}
1 \\
0 \\
-1
\end{array}\right] *\left[\begin{array}{ccc}
1 & 2 & 1
\end{array}\right]=\left[\begin{array}{ccc}
1 & 2 & 1 \\
0 & 0 & 0 \\
-1 & -2 & -1
\end{array}\right] \\
\operatorname{Sobel}_{Y}=\left[\begin{array}{c}
1 \\
2 \\
1
\end{array}\right] *\left[\begin{array}{ccc}
1 & 0 & -1
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & -1 \\
2 & 0 & -2 \\
1 & 0 & -1
\end{array}\right] \\
d_{x}=f(x, y)^{*} \operatorname{Sobel}_{x}(x, y) \\
d_{y}=f(x, y)^{*} \operatorname{Sobel}_{y}(x, y)
\end{array}$$
进一步可以得到图像梯度的幅值：
$M(x, y)=\sqrt{d_{x}^{2}(x, y)+d_{y}^{2}(x, y)}$
为了简化计算，幅值也可以作如下近似：
$M(x, y)=\left|d_{x}(x, y)\right|+\left|d_{y}(x, y)\right|$
角度为：
$\theta_{M}=\arctan \left(d_{y} / d_{x}\right)$
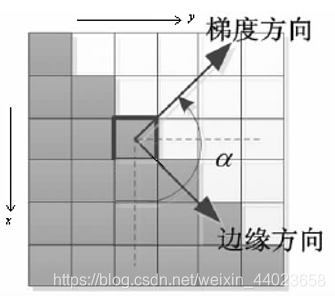
这里需要注意的是：梯度方向和图像边缘方向是互相正交的。
```python
import cv2
import numpy as np
# Read image
img = cv2.imread('E:/python-project/deep-learning/picture/test1.jpg')
img = np.float32(img) / 255.0 # 归一化
# 计算x和y方向的梯度
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)
# 计算合梯度的幅值和方向（角度）
mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
```
**计算梯度直方图**
经过上一步计算，每一个像素点都会有两个值：梯度幅值/梯度方向。
在这一步中，图像被分成若干个8×8的cell，例如我们将图像resize至64x128的大小，那么这幅图像就被划分为8x16个8x8的cell单元，并为每个8×8的cell计算梯度直方图。当然，cell的划分也可以是其他值：16x16，8x16等，根据具体的场景确定。
在计算梯度直方图，让我们先了解一下为什么我们将图像分成若干个cell?
这是因为如果对一整张梯度图逐像素计算，其中的有效特征是非常稀疏的，不但运算量大，而且会受到一些噪声干扰。于是我们就使用局部特征描述符来表示一个更紧凑的特征，计算这种局部cell上的梯度直方图更具鲁棒性。
以8x8的cell为例，一个8x8的cell包含了8x8x2 = 128个值，因为每个像素包括梯度的大小和方向。
在HOG中，每个8x8的cell的梯度直方图本质是一个由9个数值组成的向量， 对应于0、20、40、60…160的梯度方向(角度)。那么原本cell中8x8x2 = 128个值就由长度为9的向量来表示，用这种梯度直方图的表示方法，大大降低了计算量，同时又对光照等环境变化更加地鲁棒。
首先，看下图：
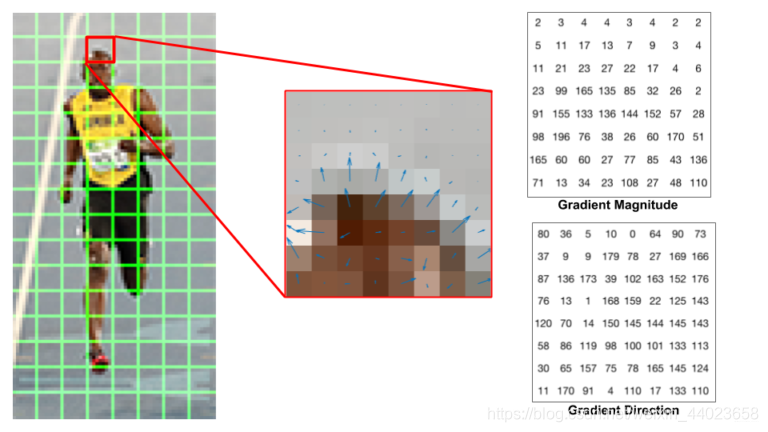
左图是衣服64x128的图像，被划分为8x16个8x8的cell；中间的图像表示一个cell中的梯度矢量，箭头朝向代表梯度方向，箭头长度代表梯度大小。
右图是 8×8 的cell中表示梯度的原始数值，注意角度的范围介于0到180度之间，而不是0到360度， 这被称为“无符号”梯度，因为两个完全相反的方向被认为是相同的。
接下来，我们来计算cell中像素的梯度直方图，将0-180度分成9等份，称为9个bins，分别是0，20，40...160。然后对每个bin中梯度的贡献进行统计：
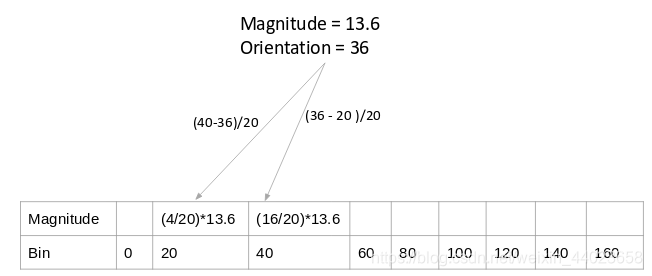
统计方法是一种加权投票统计， 如上图所示，某像素的梯度幅值为13.6，方向为36，36度两侧的角度bin分别为20度和40度，那么就按一定加权比例分别在20度和40度对应的bin加上梯度值，加权公式为：
40度对应的bin：(（40-36）/20) * 13.6，分母的20表示20等份，而不是20度；
20度对应的bin：(（36-20）/20) * 13.6，分母的20表示20等份，而不是20度；
还有一个细节需要注意，如果某个像素的梯度角度大于160度，也就是在160度到180度之间，那么把这个像素对应的梯度值按比例分给0度和160度对应的bin。如左下图绿色圆圈中的角度为165度，幅值为85，则按照同样的加权方式将85分别加到0度和160度对应的bin中。
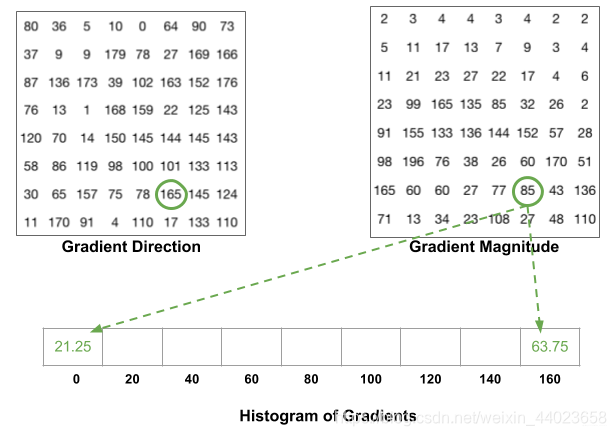
对整个cell进行投票统计，正是在HOG特征描述子中创建直方图的方式，最终得到由9个数值组成的向量—梯度方向图：
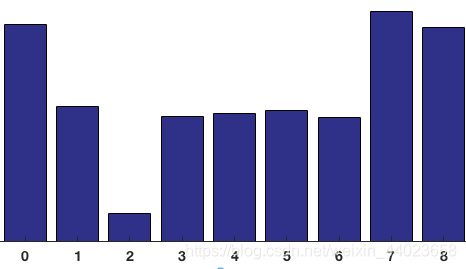
**Block 归一化**
HOG特征将8×8的一个局部区域作为一个cell，再以2×2个cell作为一组，称为一个block，也就是说一个block表示16x16的区域。
我们可能会想，为什么又需要分block呢？
这是因为，虽然我们已经为图像的8×8单元创建了HOG特征，但是图像的梯度对整体光照很敏感。这意味着对于特定的图像，图像的某些部分与其他部分相比会非常明亮。
我们不能从图像中完全消除这个。但是我们可以通过使用16×16个块来对梯度进行归一化来减少这种光照变化。
由于每个cell有9个值，一个block（2×2个cell）则有36个值，HOG是通过滑动窗口的方式来得到block的.
前面已经说明，归一化的目的是为了降低光照的影响，因为梯度对整体光照非常敏感，比如通过将所有像素值除以2来使图像变暗，那么梯度幅值将减小一半，因此直方图中的值也将减小一半，我们就需要将直方图“归一化”。
归一化的方法有很多：L1-norm、L2-norm、max/min等等，一般选择L2-norm。
例如对于一个[128，64，32]的三维向量来说，模长是$\sqrt{128^2+64^2+32^2}=146.64$，这叫做向量的L2范数。将这个向量的每个元素除以146.64就得到了归一化向量 [0.87, 0.43, 0.22]。
采用同样的方法，一个cell有一个梯度方向直方图，包含9个数值，一个block有4个cell，那么一个block就有4个梯度方向直方图，将这4个直方图拼接成长度为36的向量，然后对这个向量进行归一化。
而每一个block将按照上图滑动的方式进行重复计算，直到整个图像的block都计算完成。
**获得HOG描述子**
每一个16 * 16大小的block将会得到一个长度为36的特征向量，并进行归一化。 那会得到多少个特征向量呢？
例如，对于上图被划分8 * 16个cell ，每个block有2x2个cell的话，那么cell的个数为：(16-1)x(8-1)=105。即有7个水平block和15个竖直block。
每个block有36个值，整合所有block的特征值，最终获得由36 * 105=3780个特征值组成的特征描述符，而这个特征描述符是一个一维的向量，长度为3780。
获得HOG特征向量，就可以用来可视化和分类了。对于多维的HOG特征，SVM就可以排上用场了。
## 4.3 基于OpenCV的实现
```python
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
if __name__ == '__main__':
src = cv.imread("E:/python-project/deep-learning/picture/test7.jpg")
cv.imshow("input", src)
hog = cv.HOGDescriptor()
hog.setSVMDetector(cv.HOGDescriptor_getDefaultPeopleDetector())
# Detect people in the image
(rects, weights) = hog.detectMultiScale(src,
winStride=(2,4),
padding=(8, 8),
scale=1.2,
useMeanshiftGrouping=False)
for (x, y, w, h) in rects:
cv.rectangle(src, (x, y), (x + w, y + h), (0, 255, 0), 2)
cv.imshow("hog-detector", src)
cv.imwrite("hog-detector.jpg",src)
cv.waitKey(0)
cv.destroyAllWindows()
```
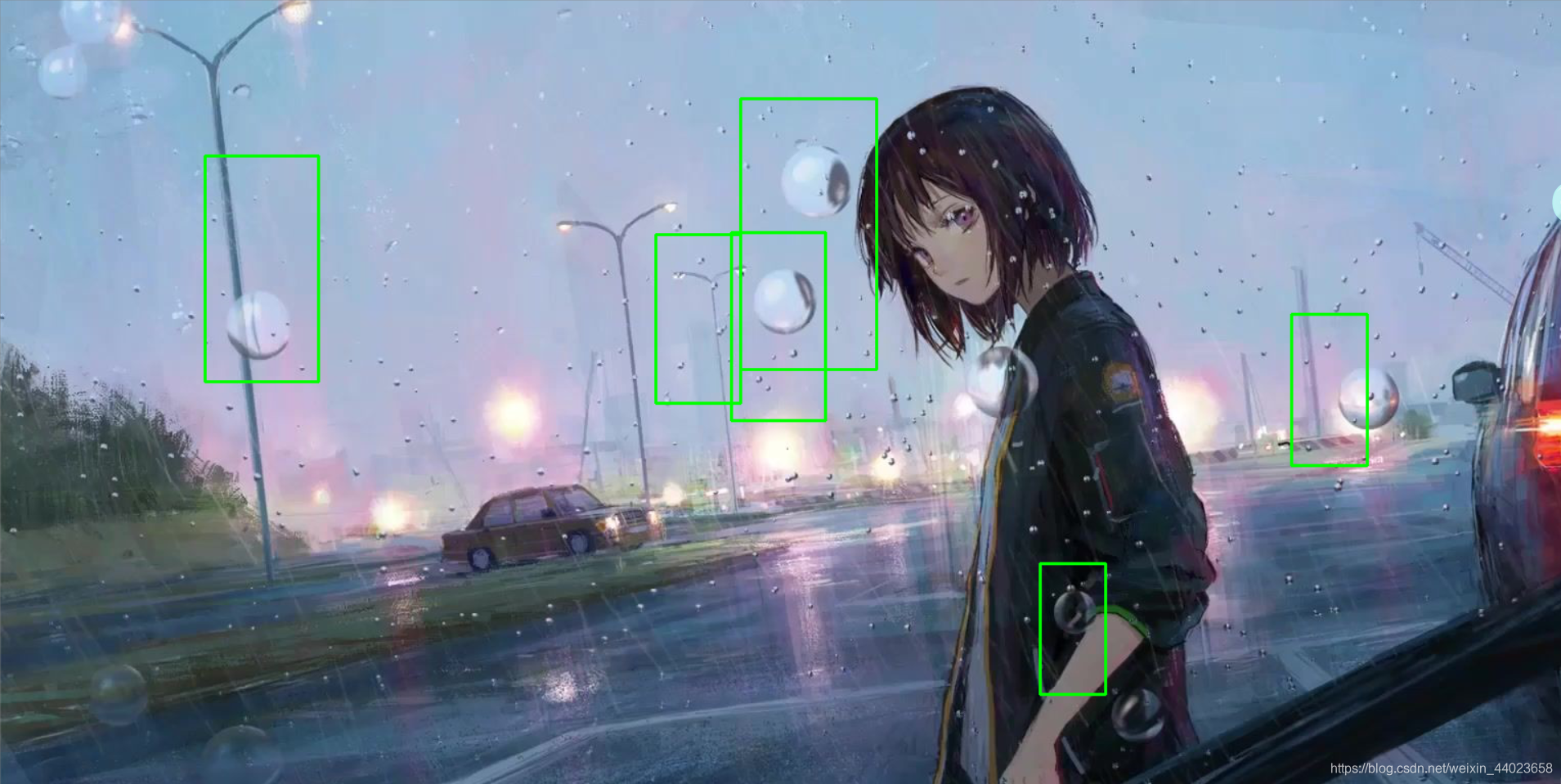效果不咋好。。。换一个
可视化：
```python
from skimage import feature, exposure
from matplotlib import pyplot as plt
import cv2
image = cv2.imread('E:/python-project/deep-learning/picture/test8.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
fd, hog_image = feature.hog(image, orientations=9, pixels_per_cell=(8, 8),
cells_per_block=(2, 4), visualise=True)
# Rescale histogram for better display
hog_image_rescaled = exposure.rescale_intensity(hog_image, in_range=(0, 10))
cv2.namedWindow("img",cv2.WINDOW_NORMAL)
cv2.imshow('img', image)
cv2.namedWindow("hog",cv2.WINDOW_NORMAL)
cv2.imshow('hog', hog_image_rescaled)
cv2.waitKey(0)==ord('q')
```
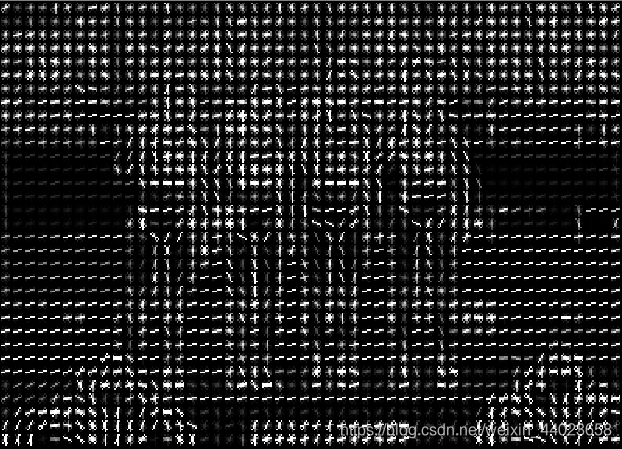
## 4.4 总结
HOG算法具有以下优点：
- HOG描述的是边缘结构特征，可以描述物体的结构信息
- 对光照影响不敏感
- 分块的处理可以使特征得到更为紧凑的表示
HOG算法具有以下缺点：
- 特征描述子获取过程复杂，维数较高，导致实时性差
- 遮挡问题很难处理
- 对噪声比较敏感
论文地址：[Histograms of Oriented Gradients for Human Detection - 2005CVPR](https://hal.inria.fr/file/index/docid/548512/filename/hog_cvpr2005.pdf)
