动态规划中滚动数组的使用

题目

64. 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

思路

因为每次只能向下或者向右，那么达到一个点的路径只有两种，要么是从上面往下，要么是从左边往右，那么问题就分解成从起点到达上面那个点的最小路径和问题，以及从起点到达左边那个点的最小路径和问题，同时考虑一下边界问题，第一行的点只能从左边往右走，第一列的点只能从上面往下走，即

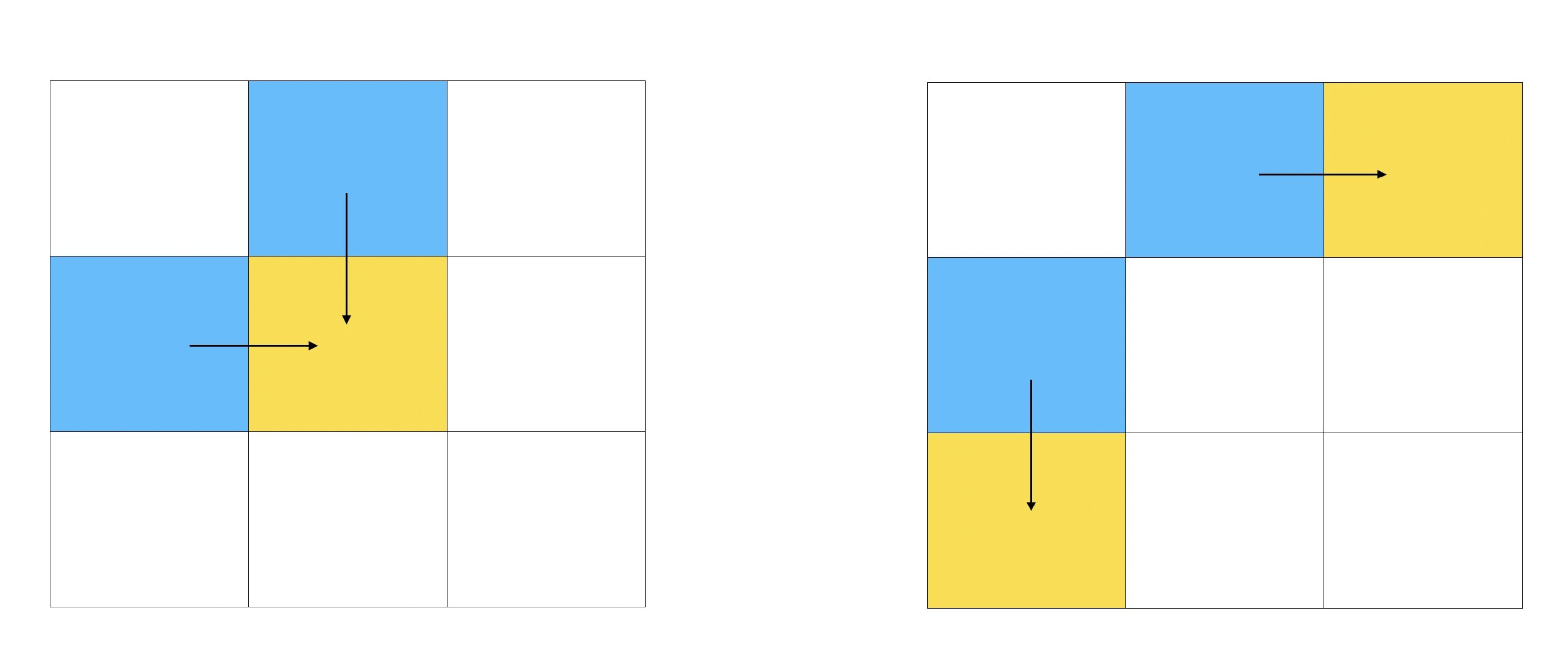
那么即刻得出以下推导公式

滚动数组压缩空间

观察上面的推导公式发现，dp[i][j]其实只与同列或者同行的上一个状态有关，这怎么理解呢

我们先看第一种情况（i > 0 且 j = 0），dp[i][0] = dp[i-1][0] + grid[i][0]，那么可以压缩成dp[i] = dp[i-1] + grid[i][0]

再看第二种情况（i = 0 且 j > 0），dp[0][j] = dp[0][j-1] + grid[0][j],，那么可以压缩成dp[j] = dp[j-1] + grid[0][j]

至于第三种情况，其实可以拆解成dp[i][j] = min(dp[i-1][j] + grid[i][j], dp[i][j-1]+grid[i][j])，即

1. dp[i][j] = dp[i-1][j] + grid[i][j]， 同一列（第j列）
2. dp[i][j] = min(dp[i][j], dp[i][j-1]+grid[i][j])，同一行（第i行）

那么就可以压缩成dp[i]=min(dp[i], dp[i-1])+grid[i][j]

这里的第二个dp[i]由于还没更新，所以此时它表示的是上一行中第i个点（正上方的Ian）的最小路径和，而dp[i-1]由于刚刚以及更新过了，所以它现在表示的是当前行的第j个点（左边的点）的最小路径和

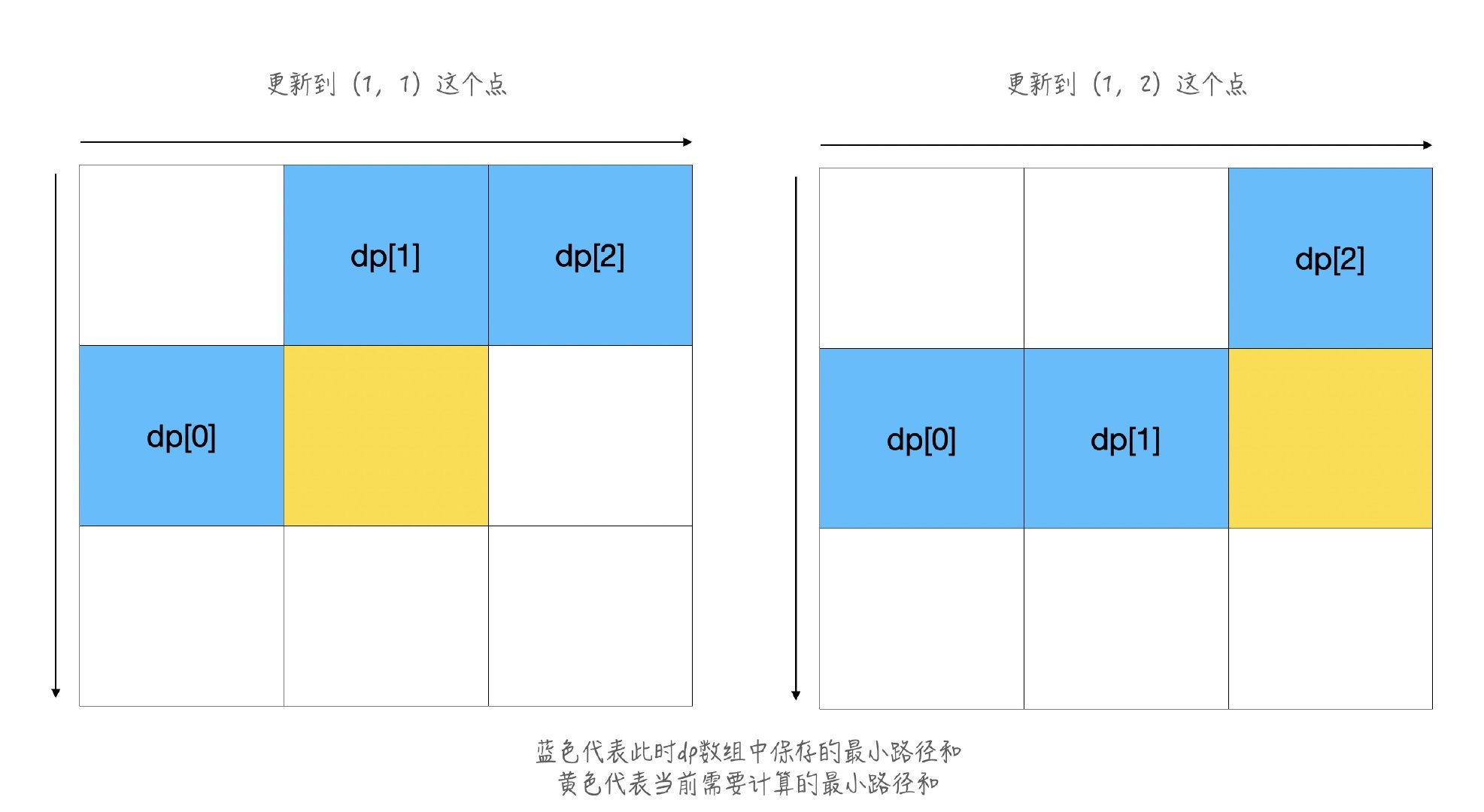
最终推导出的公式

这样就将dp从二维数组压缩成一维数组了

本文使用 mdnice 排版