前言
二叉堆是计算机科学中一种非常著名的数据结构,由于它能高效、快速地找出最大值和最小值因此常被用于优先队列和堆排序算法。
本文将详解二叉堆并用TypeScript将其实现,欢迎各位感兴趣的开发者阅读本文。
写在前面
本文重点讲解堆如何实现,对堆这种数据结构不了解的开发者请移步我的另一篇文章:数据结构:堆
实现思路
二叉堆是一种特殊的二叉树,二叉堆也叫堆,它有以下两个特性:
- 它是一颗完全二叉树
- 二叉堆不是最小堆就是最大堆
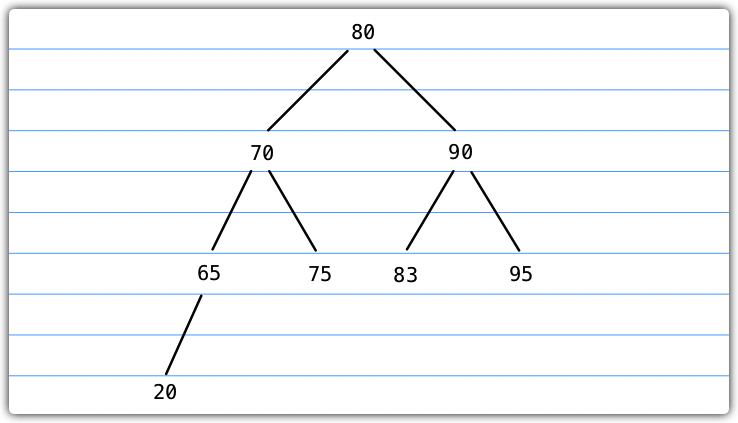
完全二叉树
一颗完全二叉树,它的每一层都有左侧和右侧子节点(除过最后一层的叶节点),并且最后一层的叶节点尽可能都是左侧子节点。
下图描述了一颗完全二叉树:
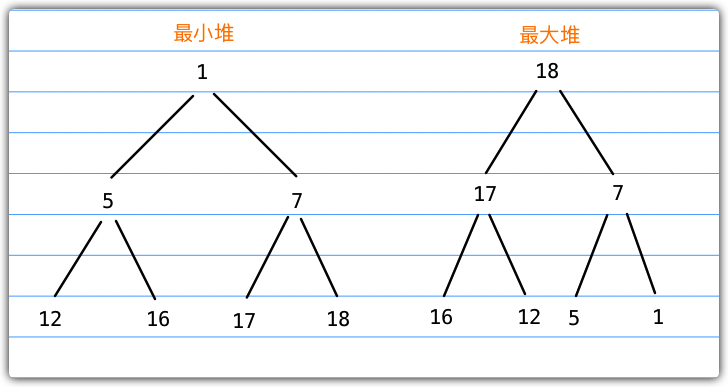
最小堆和最大堆
- 最小堆:所有的节点都小于等于它的子节点
- 最大堆:所有的节点都大于等于它的子节点
下图描述了最大堆和最小堆
实现二叉堆
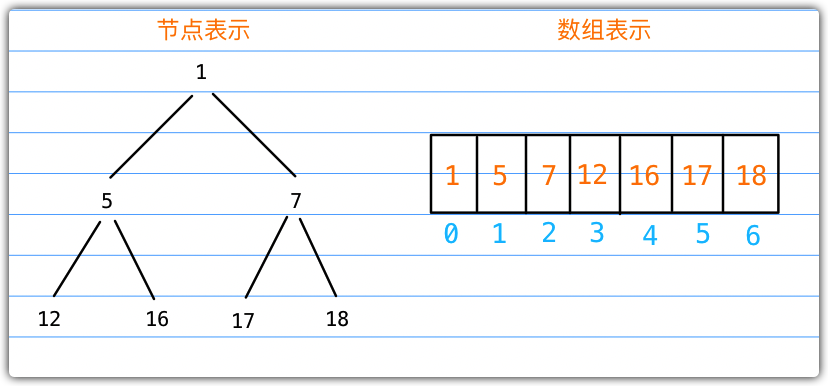
二叉堆有两种表现方式:
- 像二叉树一样用节点表示
- 使用数组表示,通过索引值检索父节点、左侧、右侧节点的值
下图描述了两种不同的表示方式
操作堆节点
我们使用数组来表示二叉堆,对于给定位置(index)的节点,我们可以对其进行如下操作:
- 获取给定节点的左侧子节点位置:2 * index + 1
- 获取给定节点的右侧子节点位置:2 * index + 2
- 获取给定节点的父节点位置:(index - 1) / 2
向堆中插入数据
向堆中插入数据(insert)是指将数据插入堆的底部叶节点再执行上移(siftUp), 表示我们将要把这个数据和它的父节点进行交换,直到父节点小于这个插入的值。
- insert方法接收一个参数:要插入的数据
- 需要对插入的数据进行非空判断,如果为null则返回false
- 数据不为空时,往数组(heap)的末尾追加要插入的数据
- 插入完成后,执行siftUp操作,将数据移动至合适的位置
- 上移完成后,则成功的向堆中插入了一条数据,返回true
上移操作的实现如下:
- siftUp方法接收一个参数:插入数据的索引位置(index)
- 获取当前要插入数据的父节点位置(parent)
- index大于0且heap[parent] > heap[index],交换parent和index位置的节点
- 更新index和parent的值,继续进行节点交换直至heap[parent] < heap[index]
交换的实现如下:
- swap接收三个参数:要操作的数组,交换的元素位置,被交换的元素位置
- 声明一个临时变量temp,赋值交换的元素
- 交换的元素赋值为被交换的元素
- 被交换的元素赋值为temp
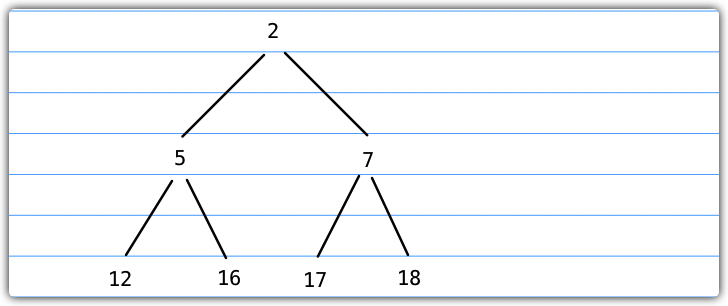
接下来我们用一个例子来描述上述插入过程,如下图所示为一个最小堆,我们要插入一个新的节点2。
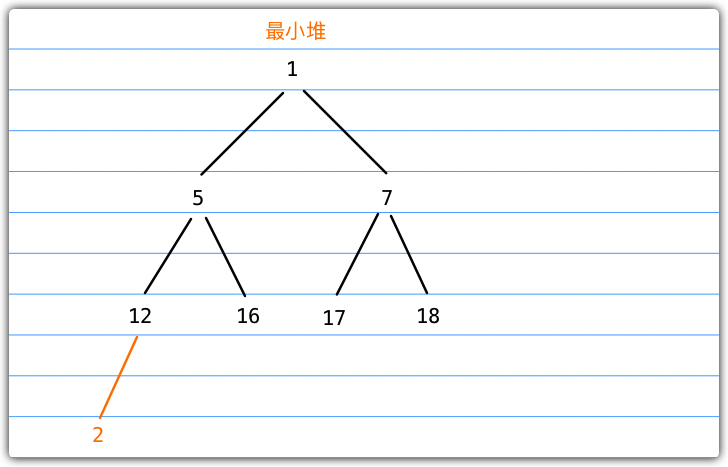
- 找到它的父节点12,比较12与2的大小,12 > 2,进行位置互换
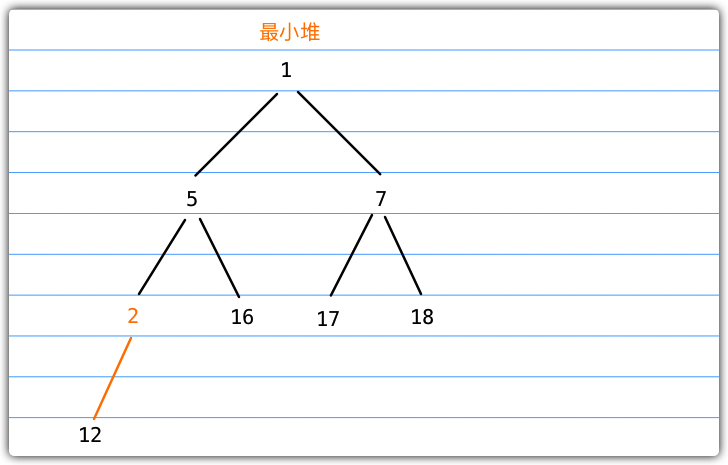
- 此时2的父节点是5,5 > 2,进行位置交换
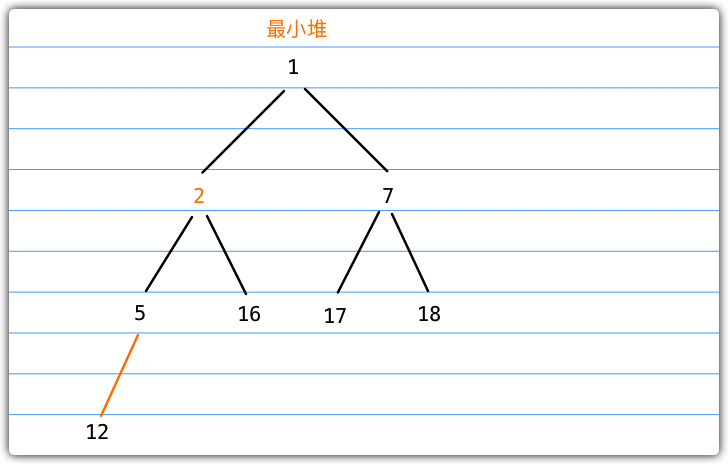
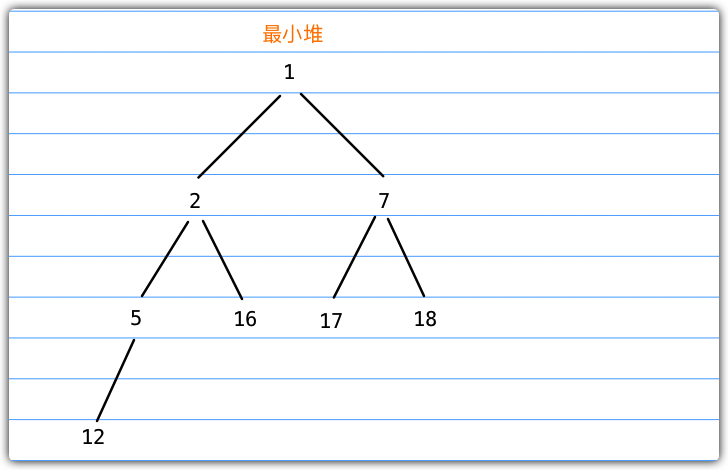
- 2此时2的父节点是1,1 < 2,插入完成
寻找堆中的最大值或最小值
- 在最小堆中数组的0号元素就是堆的最小值
- 在最大堆中数组的0号元素就是堆的最大值
导出堆中的最小值或最大值
移除最小值(最小堆)或最大值(最大堆)表示移除数组中的第一个元素(堆的根节点)。
在移除后,我们需要将堆的最后一个元素移动至根部并执行下移(siftDown)函数,表示我们将交换元素直到堆的结构正常。
- extract函数不接收参数
- 如果堆为空则返回undefined
- 如果堆的长度为1,直接返回堆顶元素
- 否则,声明一个变量保存堆顶元素
- 执行下移函数调整堆结构
- 返回刚才保存堆堆顶元素
下移操作的实现:
- siftDown函数接收一个参数:需要调整的元素位置(index)
- 声明一个变量(element)保存index
- 获取index的左子节点(left)、右子节点(right)、堆的大小(size)
- 如果heap[element] > heap[left],则更新element的值为left
- 如果heap[element] > heap[right],则更新element的值为right
- 如果index !== element,则交换index和element位置的元素,继续执行siftDown函数
接下来,我们通过一个例子来讲解上述执行过程,下图描述了一个最小堆
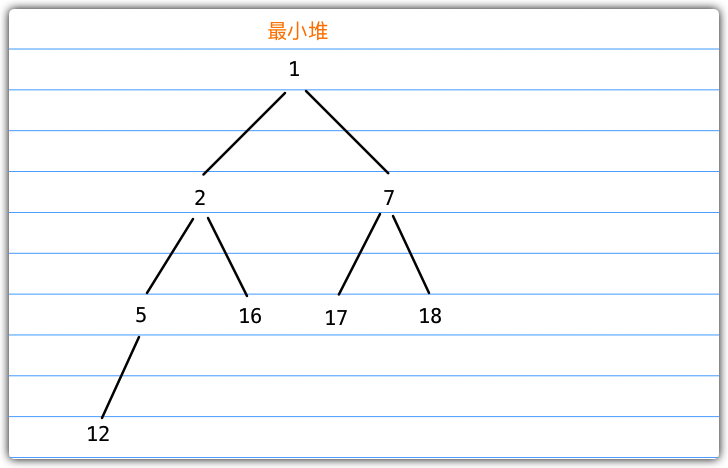
- 我们导出堆顶节点1
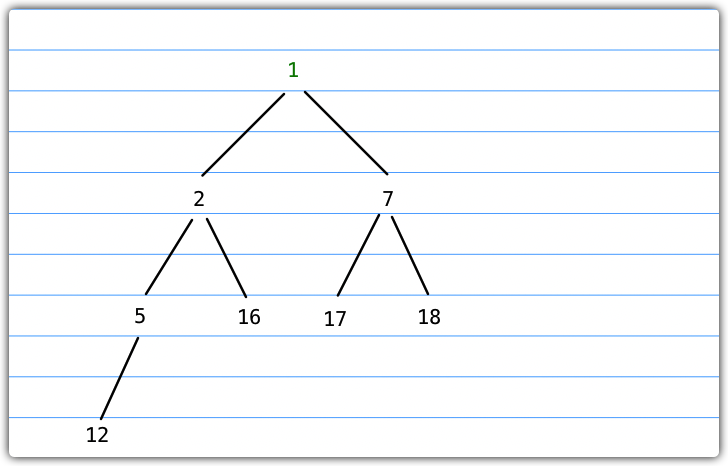
- 此时,我们需要把堆的最后一个节点放到堆顶
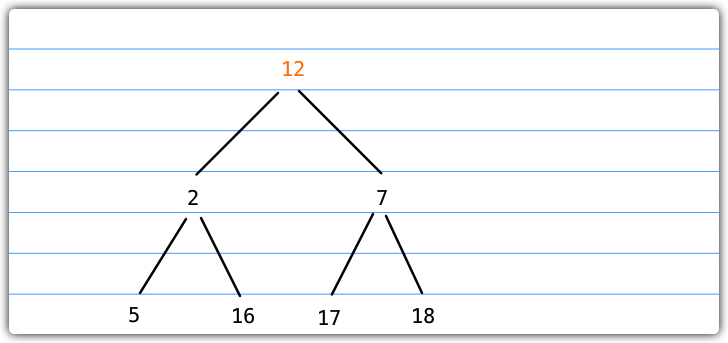
- 此时,进行下移操作,比较12和其左子节点2的大小,12 > 2,交换节点位置
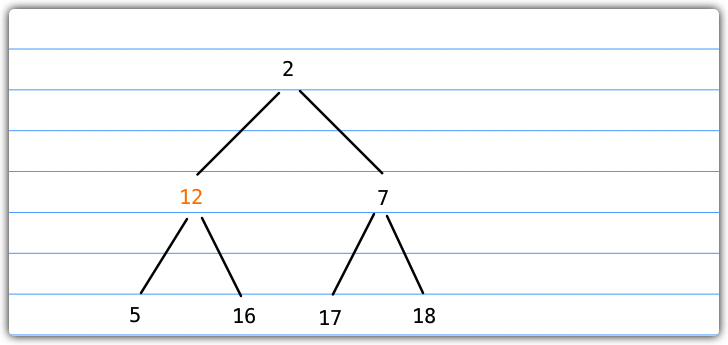
- 继续进行下移操作,比较12和其左子节点5的大小,12 > 5,交换节点位置
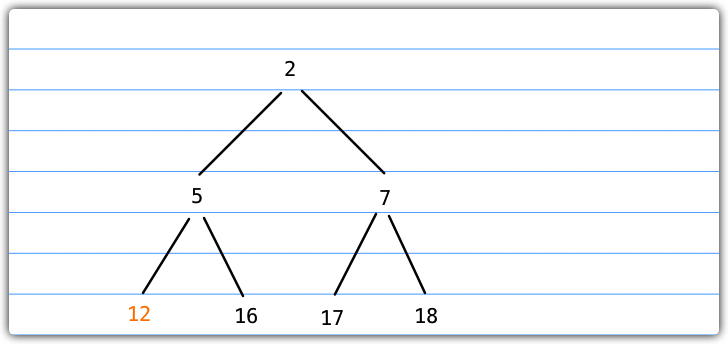
- 此时index === element,下移操作完成,堆节点导出完成
实现最大堆
上述操作我们实现了一个最小堆,最大堆与最小堆的别就在于节点的比较,因此我们只需要继承最小堆,重写比对函数,将原来的a与b比较,改为b与a比较即可。
实现代码
上面我们讲解了堆的概念,分析了的实现思路,接下来我们将上述实现思路转化为代码
- 新建Heap.ts文件
- 声明MinHeap类,声明堆、比对函数、初始化堆
export class MinHeap<T> {
// 用数组来描述一个堆
protected heap: T[];
constructor(protected compareFn: ICompareFunction<T> = defaultCompare) {
this.heap = [];
}
}
- 实现获取左、右、父节点函数
// 获取左子节点的位置
protected getLeftIndex(index: number): number {
return 2 * index + 1;
}
// 获取右子节点的位置
protected getRightIndex(index: number): number {
return 2 * index + 2;
}
// 获取父节点的位置
protected getParentIndex(index: number): number | undefined {
if (index === 0) {
return undefined;
}
return Math.floor((index - 1) / 2);
}
- 实现插入函数
insert(value: T): boolean {
if (value != null) {
// 向堆的叶结点添加元素,即数组的尾部
this.heap.push(value);
// 进行上移操作,即上移节点至合适的位置
this.siftUp(this.heap.length - 1);
return true;
}
return false;
}
// 实现上移函数
protected siftUp(index: number): void {
// 获取父节点位置
let parent = <number>this.getParentIndex(index);
// 插入的位置必须大于0,且它的父节点大于其本身就执行循环里的操作
while (index > 0 && this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN) {
// 交换元素的位置
this.swap(this.heap, parent, index);
// 修改当前插入值的位置为它的父节点,重新获取父节点的位置,即重复这个过程直到堆的根节点也经过了交换
index = parent;
parent = <number>this.getParentIndex(index);
}
}
// 实现交换数组元素位置函数
protected swap(array: T[], exchangeElement: number, exchangedElement: number): void {
// 用一个临时变量保存交换元素
const temp = array[exchangeElement];
// 将被交换元素赋值给交换元素
array[exchangeElement] = array[exchangedElement];
// 将第一步保存的临时变量赋值给被交换元素
array[exchangedElement] = temp;
}
- 实现寻找堆的最小值函数
findMinimum(): T | undefined {
// 返回数组的最小元素
return this.isEmpty() ? undefined : this.heap[0];
}
// 判断堆是否为空
isEmpty(): boolean {
return this.size() === 0;
}
- 实现导出堆的最小值函数
extract(): T | undefined {
if (this.isEmpty()) {
return undefined;
}
if (this.size() === 1) {
// 返回数组的第一个元素
return this.heap.shift();
}
const removedValue = this.heap.shift();
// 执行下移操作
this.siftDown(0);
return removedValue;
}
// 下移操作
protected siftDown(index: number): void {
// 保存当前插入值的位置
let element = index;
// 获取其左、右子节点的位置
const left = this.getLeftIndex(index);
const right = this.getRightIndex(index);
const size = this.size();
// 元素有效,且当前元素大于其左子节点
if (left < size && this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN) {
element = left;
}
// 元素有效,当前元素大于其右子节点
if (right < size && this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN) {
element = right;
}
// 找到最小子节点的位置,校验它的值是否和element相同
if (index !== element) {
// 如果不相同将它和最小的element进行交换
this.swap(this.heap, index, element);
// 递归执行
this.siftDown(element);
}
}
完整代码地址:Heap.ts
堆排序
堆的一种应用就是堆排序,此处不讲解堆排序的实现思路,对堆排序不了解的开发者请移步我的另一篇文章: 排序算法:堆排序的理解与实现
- 实现堆排序函数
heapSort(array: T[]): void {
// 构建堆
this.buildHeap(array);
// 从堆的末尾开始遍历,将遍历到的元素与0好元素进行交换,然后执行下移操作
for (let i = array.length - 1; i >= 0; i--) {
this.swap(array, i, 0);
this.heapify(array, i, 0);
}
}
// 构建堆
private buildHeap(array: T[]) {
// 获取最后一个节点的位置
const last = array.length - 1;
const lastParent = <number>this.getParentIndex(last);
// 从最后一个节点的父节点开始进行heapify操作
for (let i = lastParent; i >= 0; i--) {
this.heapify(array, array.length, i);
}
}
// 交换节点
private heapify(array: T[], size: number, index: number) {
// 递归基线条件
if (index >= size) {
return false;
}
// 找到当前要操作节点的左、右子树
const left = this.getLeftIndex(index);
const right = this.getRightIndex(index);
// 保存当前要操作节点的位置
let element = index;
// 如果当前要操作节点的左子节点大于其父节点,更新element的值
if (left < size && this.compareFn(array[left], array[element]) === Compare.BIGGER_THAN) {
element = left;
}
// 如果当前要操作节点的右子节点大于其父节点,更新element的值
if (right < size && this.compareFn(array[right], array[element]) === Compare.BIGGER_THAN) {
element = right;
}
// element的位置不等于当前要操作节点,交换元素位置,递归执行
if (element !== index) {
this.swap(array, element, index);
this.heapify(array, size, element);
}
}
编写测试代码
接下来我们测试下上述代码是否正常执行
import { MinHeap, MaxHeap } from "./lib/Heap.ts";
const minHeap = new MinHeap();
minHeap.insert(13);
minHeap.insert(10);
minHeap.insert(5);
minHeap.insert(7);
minHeap.insert(4);
minHeap.insert(17);
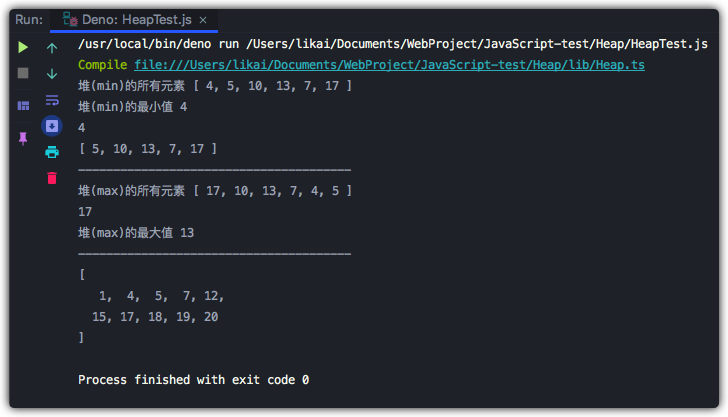
console.log("堆(min)的所有元素", minHeap.getIsArray());
console.log("堆(min)的最小值", minHeap.findMinimum());
console.log(minHeap.extract());
console.log(minHeap.getIsArray());
console.log("---------------------------------------");
const maxHeap = new MaxHeap();
maxHeap.insert(13);
maxHeap.insert(10);
maxHeap.insert(5);
maxHeap.insert(7);
maxHeap.insert(4);
maxHeap.insert(17);
console.log("堆(max)的所有元素", maxHeap.getIsArray());
console.log(maxHeap.extract());
console.log("堆(max)的最大值", maxHeap.findMinimum());
console.log("---------------------------------------");
const arrayTest = [12, 15, 17, 18, 4, 5, 1, 7, 19, 20];
minHeap.heapSort(arrayTest);
console.log(arrayTest);
写在最后
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于掘金,未经许可禁止转载💌