这一段时间在学习OpenGL，也把大学的时代的图形学又拉出来重见了天日，写篇博客记录，日后回头查找也算是有个谱。因为是做iOS，本身也是为了研究iOS的音视频，所以用Xcode来编写，语言还是C。配图尽量绘制，有部分借用了CC和endl的图，已注明。

图形学相关的数学知识

OpenGL中，我们知道有模型矩阵、视图矩阵和投影矩阵，要进行变换（平移动、缩放、旋转等其他变换）时有模型变换、视图变换等等，这个变换过程，使用的就是矩阵的乘法。

向量

向量是个有方向的矢量，是个抽象的东西，无论是在二维的笛卡尔坐标系还是三维坐标系中，都可以有向量。通过向量，我们可以指定、知道、变换 顶点、图形、3D物体的位置。在三维坐标系中，一个顶点P就是空间坐标系（三维坐标系）的一个位置，而这个位置就是由（x,y,x）构成，而（x,y,x）就是一个向量,下面是一个向量a在三维坐标中的展 a = x+y+z,

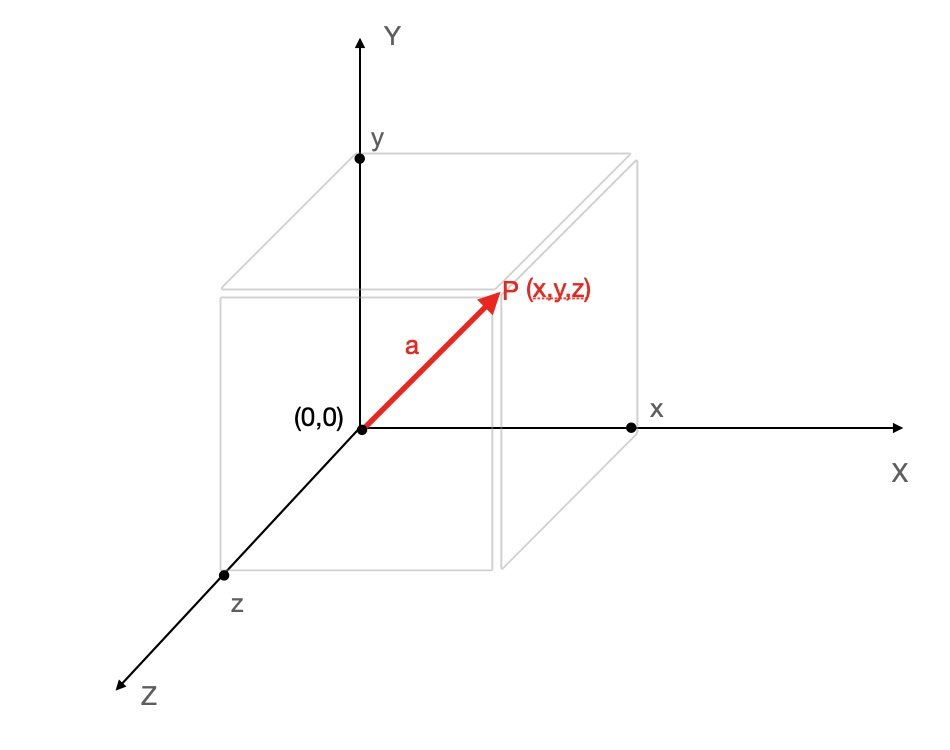
在X轴上的投影就是在X轴上的分向量(x,0,0)，在Y轴上的分向量(0,y,0),在Z轴上的分向量(0,0,z)。

向量a用矩阵表示就是

a=\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}

在OpenGL中如何表示、创建向量：

math3d库，有2个数据类型，能够表示⼀一个三维或者四维向量量。 M3DVector3f可以表示⼀一个三维向量量(x,y,z)， M3DVector4f则可以表示⼀一个四维向量量(x,y,z,w). 在典型情况下，w坐标设为1.0。x,y,z值通过除以w，来进⾏行行缩放。⽽而除以1.0则本质上不不改变x,y,z值。

//三维向量量/四维向量量的声明
typedef float M3DVector3f[3]; 
typedef float M3DVector4f[4];
//声明⼀一个三维向量量 M3DVector3f:类型 vVector:变量量名 
M3DVector3f vVector;
//声明⼀一个四维向量量并初始化⼀一个四维向量量
M3DVector4f vVertex = {0,0,1,1};
//声明⼀一个三分量量顶点数组，例例如⽣生成⼀一个三⻆角形 
// M3DVector3f vVerts[] = {-0.5f,0.0f,0.0f, 0.5f,0.0f,0.0f, 0.0f,0.5f,0.0f};

单位向量

单位向量：向量的模为1的向量。换句话说，也就是移动了向量，使得从原点开始向量的模=向量的长度 = $\sqrt{x^{2}+y^{2}+z^{2}}$

点乘（dot product）

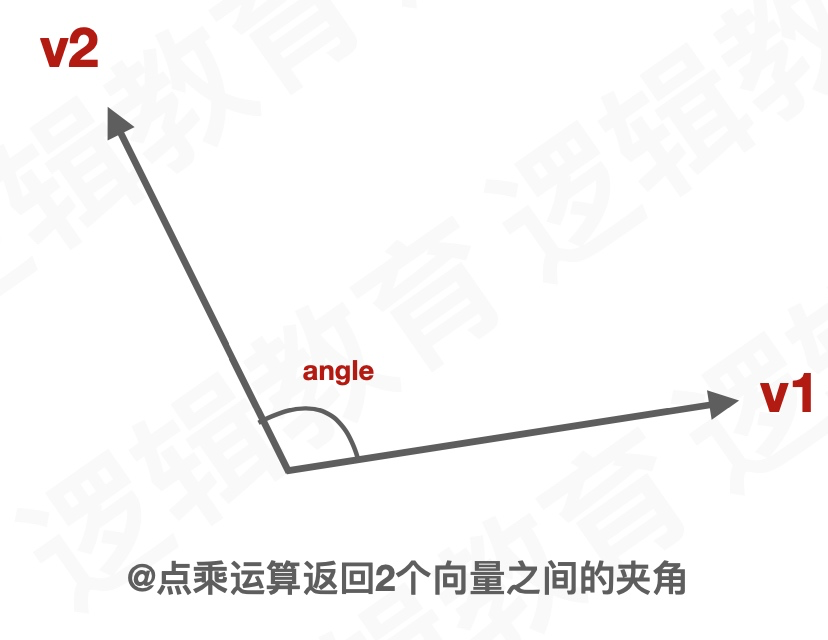
2个（三维向量）单元向量之间进行点乘，得到一个标量，表示2个向量之间的夹角。如何单位化向量？（x/模,y/模,z/模）即是方向相同的单位向量。

OpenGL也提供了API：

//1.m3dDotProduct3 函数获得2个向量量之间的点乘结果;
float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v);

//2.m3dGetAngleBetweenVector3 即可获取2个向量量之间夹⻆角的弧度值; 
float m3dGetAngleBetweenVector3(const M3DVector3f u,const
M3DVector3f v);

差乘

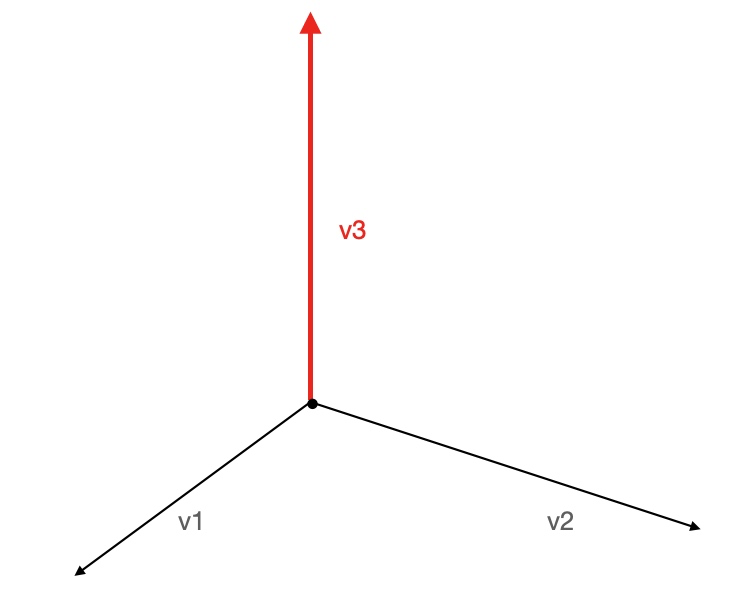
2个单位向量v1和v2差乘，会得到一个分别垂直于这2个向量（也就是垂直于v1和v2所构成的平面）的新向量v3

在OpenGL中提供运算API

//1.m3dCrossProduct3 函数获得2个向量量之间的叉乘结果得到⼀一个新的向量量
void m3dCrossProduct3(M3DVector3f result,const M3DVector3f  u ,const
    M3DVector3f v);

矩阵

矩阵 (下面这些都是矩阵的样子，二维结构，有行有列，至少1行或者1列)

\begin{pmatrix}
1 & 2 \\
3 & 4 \\
5 & 6 \\
\end{pmatrix}、
\begin{pmatrix}
1 \\
2 \\
3 \\
\end{pmatrix}、
\begin{pmatrix}
1 & 2 & 3 \\
\end{pmatrix}、
\begin{pmatrix}
1 & 2 & 20 & 12 \\
3 & 4 & 40 & 13 \\
5 & 6 & 50 & 14 \\
\end{pmatrix}

矩阵的乘法

设A为 m行 * p列的矩阵，B为 p行 * n列的矩阵，那么称 m * n 的矩阵C为矩阵A与B的乘积，记作 C=AB，（不是）。注意：A的列数要和B行数一致，都为p，否则无法运算！ 举例说明两个矩阵的相乘

来个具体的场景：A矩阵和B矩阵，等为了更直观看到操作的数，C中的A1就表示A矩阵中的1，

A=\begin{pmatrix}
1 & 2 \\
3 & 4 \\
5 & 6 \\
\end{pmatrix} ，
B=\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{pmatrix}

C=\begin{pmatrix}
A1*B1+A2*B4, & A1*B2+A2*B5 & A1*B3+A2*B6 \\
A3*B1+A4*B4, & A3*B2+A4*B5 & A3*B3+A4*B6 \\
A5*B1+A6*B4, & A5*B2+A6*B5 & A5*B3+A6*B6 \\
\end{pmatrix}

我们发现一个规律：A的i行向量与B的j列向量点乘，放入C的(i,j)位置。

借用一下endl的图

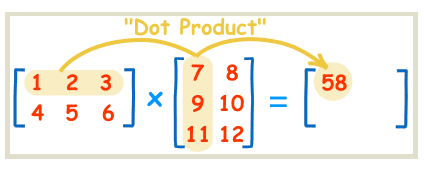
用伪代码来看：

// 这是一个行优先演示
// m:A行数 上图A有3行
// n:B列数 上图B有3列
for (i=0,i<m，i++): 
    row[p] = A[i] ; // row是A的第i行,每一行的元素数就是A的列数
    for (j=0,j<n,j++):
        column[p] = B[j];// column是B的第j列，每一列的元素数就是B的行数
        C[i][j] = row[0]+column[0]+...+row[p-1]+column[p-1]; // A的第i行向量与当前B的第j列向量进行点乘：每一位元素分别相乘（都是有p个元素），再求和，即是C[i][j]位置的值

所以我们要求两个矩阵一定要满足一个特性才能运算：A(m*p)的列数一定要等于B( p *n)的行数，都是p。

在OpenGL中如何定义矩阵

//三维矩阵/四维矩阵的声明
typedef float M3DMatrix33f[9];
typedef float M3DMatrix44f[16];

OpenGL并没有按照矩阵的二维结构以二维数组来存储，反而用了一维数组，在OpenGL里，使用以列为主的矩阵排序。矩阵的转置。

经常听到的OpenGL中的“变换”是什么

---	---
视图变换	指定观察者位置
模型变换	在场景中移动物体：移动、放大、缩小、旋转物体
投影变换	改变视景体⼤小和设置它的投影方式
视口变换	伪变化,对窗⼝上最终输出进行缩放

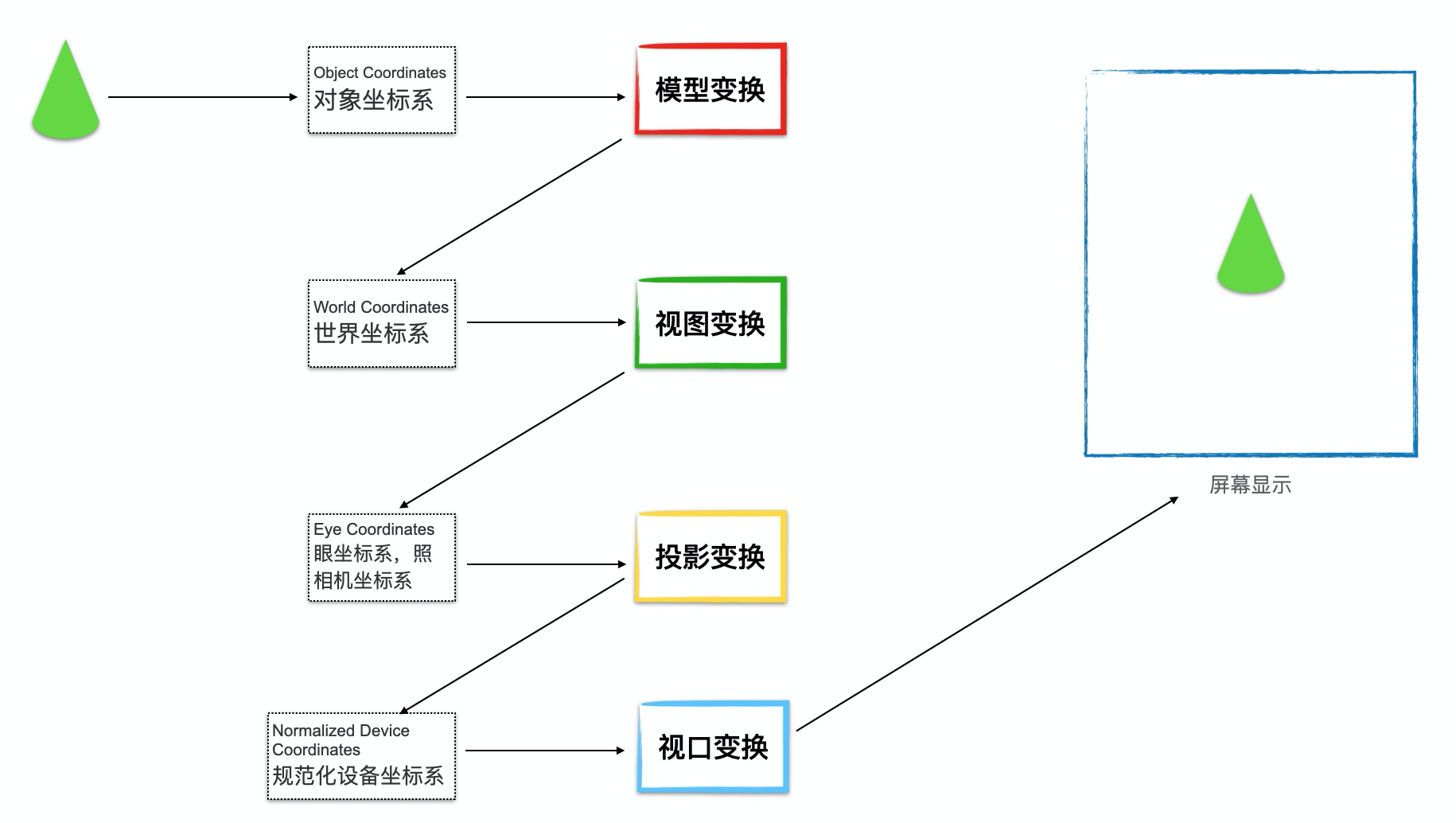
对物体的变换本质是对顶点的变换，在OpenGL中，变换顶点向量要按照以下规则： 变换顶点向量 = M_pro * M_view * M_model * V_local M_pro投影矩阵 M_view视图矩阵 M_model模型矩阵 V_local顶点经过上述矩阵计算后，就得到了变换后的顶点向量，完成变换。

模型变换：

⽤于操纵模型与其中某特定变换. 这些变换将对象移动到需要的位置. 通过旋转,缩放,平移.

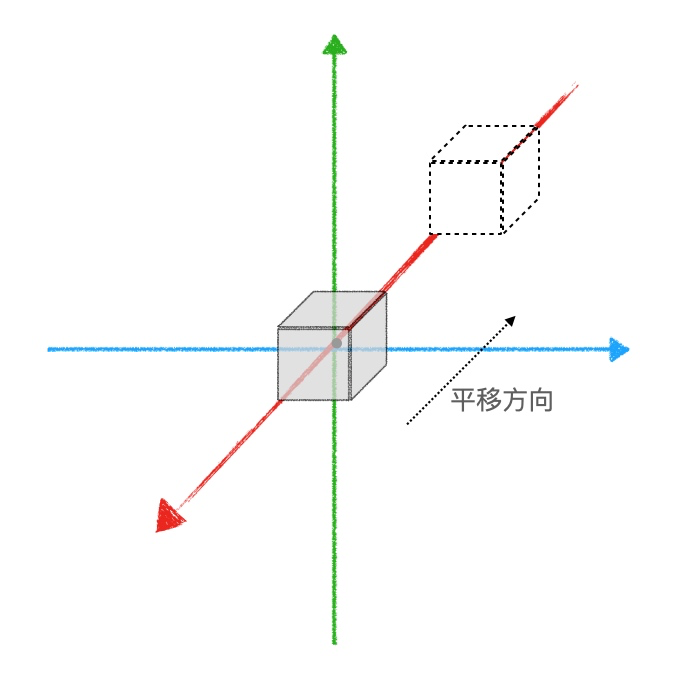
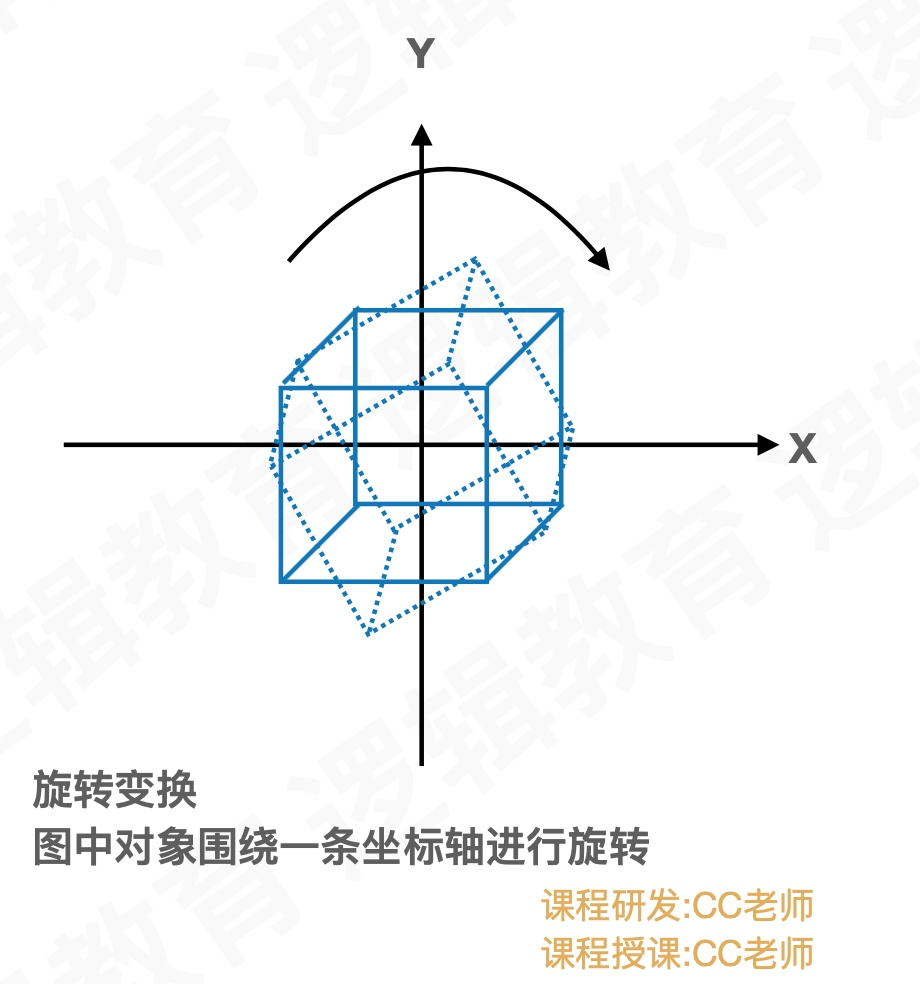
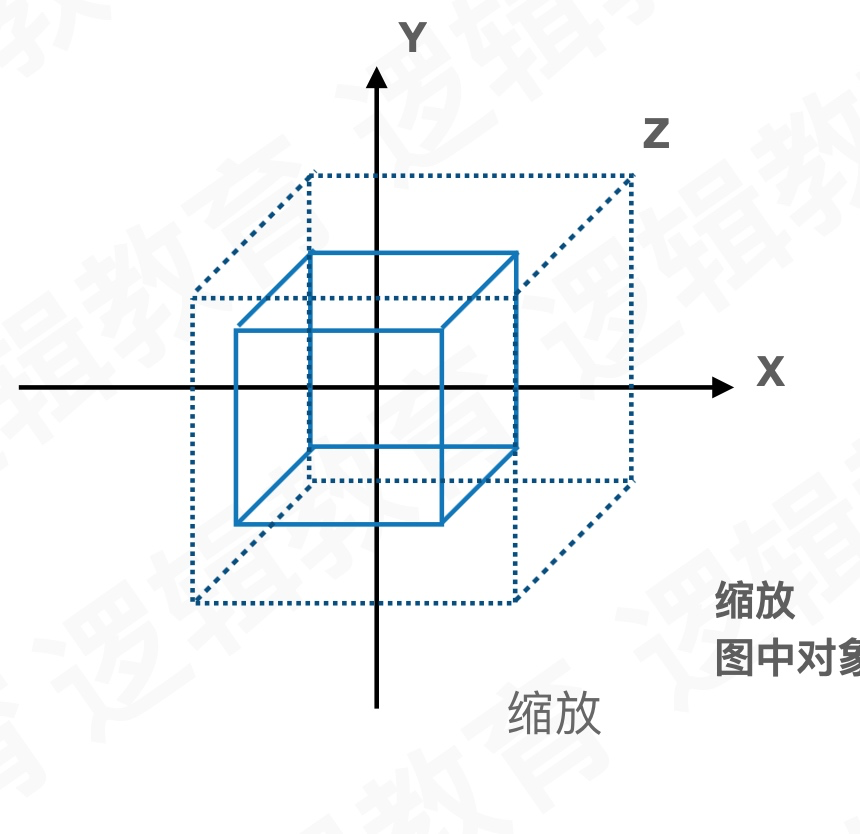
OpenGL中平移、旋转、缩放的API及举例演示

平移

void m3dTranslationMatrix44(M3DMatrix44f m, floata x, float y, float z);

举例1：沿着Y轴平移10个单位的距离

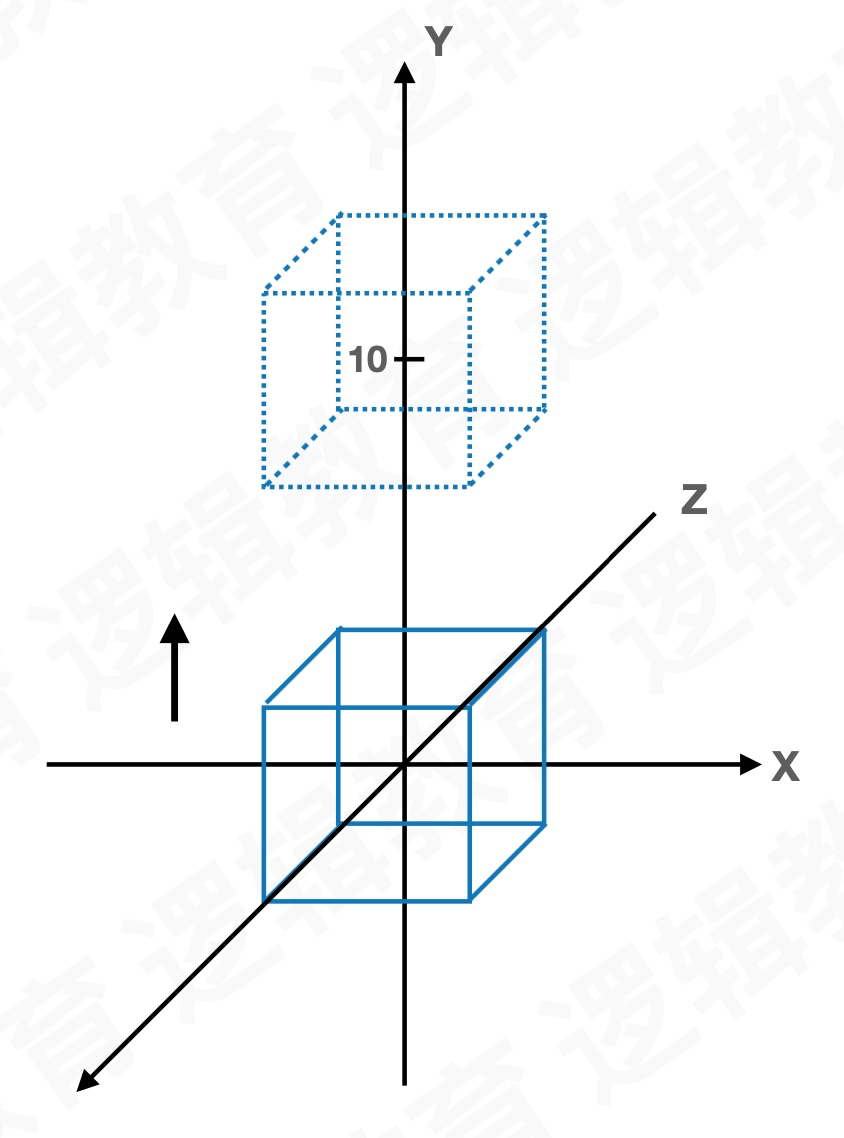
代码：m3dTranslationMatrix44(m,0,10,0);

举例2:沿着空间任意方向移动如下图，黑点是立体的中心点

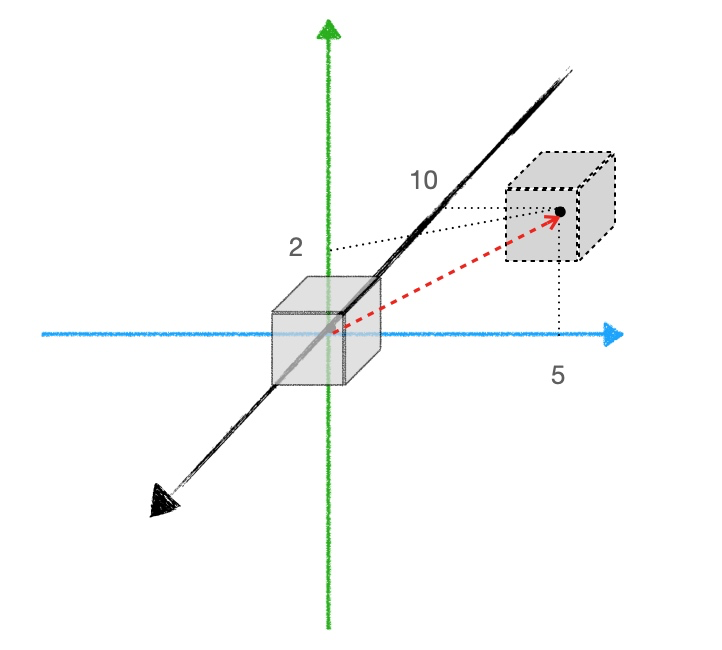
// 投影在X轴上移动了5个单位距离，投影在Y轴上移动了2个单位距离，在Z轴上移动了10个单位距离 // 其实，x,y,x 就是移动方向的向量 m3dTranslationMatrix44(m,5,2,20);

旋转

// angle:旋转的弧度 正数时逆时针旋转，负数时顺时针旋转
// 当x=1 y=0 z=0 ，围绕X轴旋转
// 当x=0 y=1 z=0 ，围绕Y轴旋转
// 当x=0 y=0 z=1 ，围绕Z轴旋转
// m则是根据 (angle,x,y,z)得到的旋转矩阵
void m3dRotationMatrix44(M3DMatrix44f m,float angle, floata x, float y, float z);

举例1：围着Y轴转45度 m3dRotationMatrix44( m3dDegToRad(45),0,1,0);

缩放

// xScale：X方向的缩放比例
// yScale：Y方向的缩放比例
// zScale：Z方向的缩放比例
void m3dScaleMatrix44(M3DMatrix44f m, floata xScale, float yScale, float zScale);

综合变换

// product模型视图矩阵，根据a变换矩阵和b变换矩阵左乘所得
// a变换矩阵，先要进行的变换
// b变换矩阵，后进行的变换
void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b)

有如下图需要变换：沿Z轴负方向移动，然后沿Y旋转

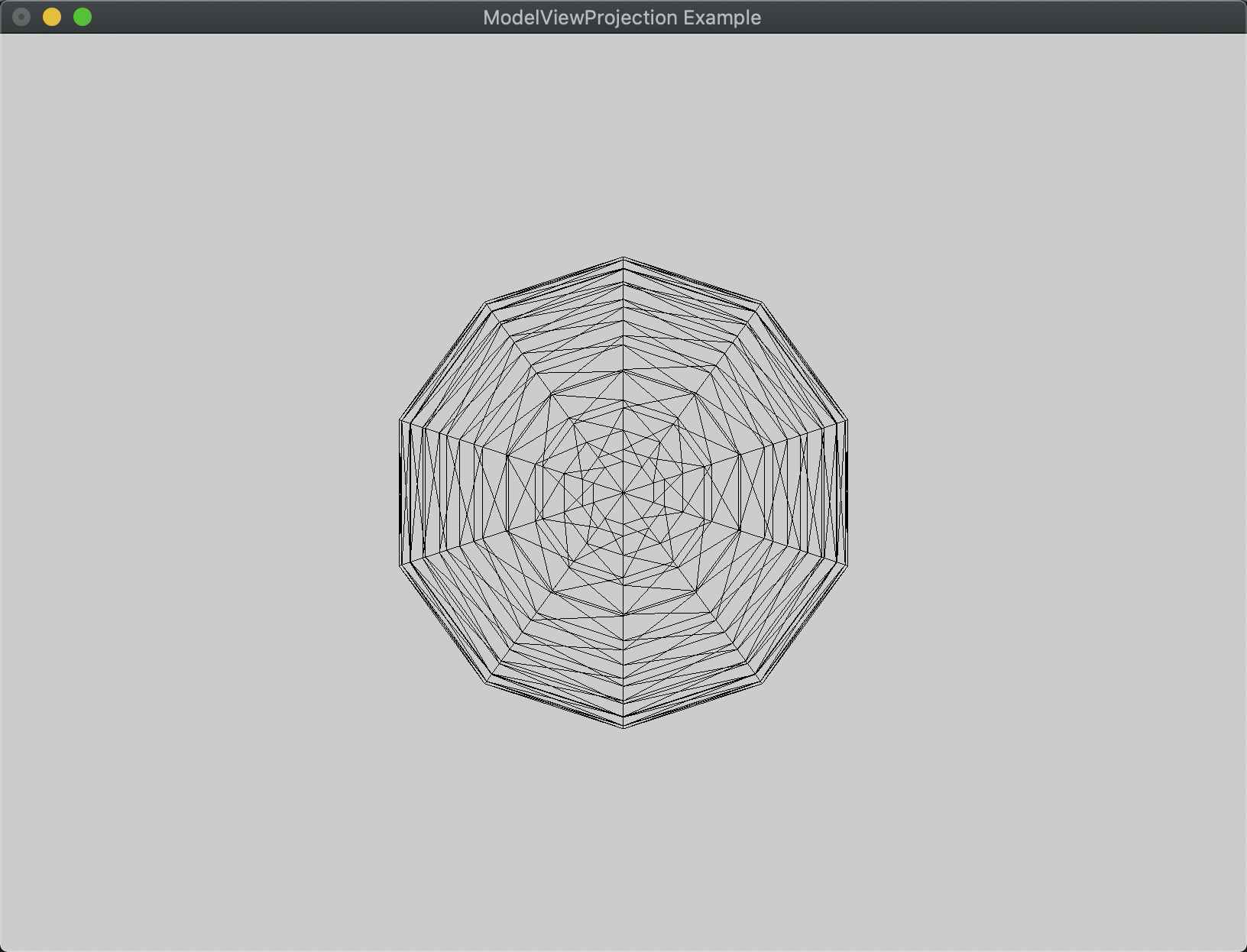
案例代码：导入的头文件，OpenGL注册的一些回调方法：设置视口和投影矩阵、初始化函数、主函数等

#include "GLTools.h"	
#include "GLMatrixStack.h"
#include "GLFrame.h"
#include "GLFrustum.h"
#include "GLGeometryTransform.h"
#include "GLBatch.h"
#include "StopWatch.h"

#include <math.h>
#ifdef __APPLE__
#include <glut/glut.h>
#else
#define FREEGLUT_STATIC
#include <GL/glut.h>
#endif


GLFrustum           viewFrustum;
GLShaderManager     shaderManager;
GLTriangleBatch     torusBatch;
GLGeometryTransform transformPipeline;

// 设置视口和投影矩阵
void ChangeSize(int w, int h)
{
    //防止除以零
    if(h == 0)
        h = 1;
    
    //将视口设置为窗口尺寸
    glViewport(0, 0, w, h);
    
    //设置透视投影
    viewFrustum.SetPerspective(35.0f, float(w)/float(h), 1.0f, 1000.0f);
}

void SetupRC()
{
    //1.
    glClearColor(0.8f, 0.8f, 0.8f, 1.0f );
    shaderManager.InitializeStockShaders();
    glEnable(GL_DEPTH_TEST);
   
    //2.形成一个球
    gltMakeSphere(torusBatch, 0.4f, 10, 20);
    glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
}



int main(int argc, char* argv[])
{
    gltSetWorkingDirectory(argv[0]);
    
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH | GLUT_STENCIL);
    glutInitWindowSize(800, 600);
    glutCreateWindow("ModelViewProjection Example");
    glutReshapeFunc(ChangeSize);
    glutDisplayFunc(RenderScene);
    
    
    GLenum err = glewInit();
    if (GLEW_OK != err) {
        fprintf(stderr, "GLEW Error: %s\n", glewGetErrorString(err));
        return 1;
    }
    
    SetupRC();
    
    glutMainLoop();
    return 0;
}

下面是核心本次综合变换案例的核心函数，也是OpenGL glutDisplayFunc(RenderScene)注册的显示绘制函数

void RenderScene(void)
{
    //清除屏幕、深度缓存区
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    
    //1.建立基于时间变化的动画
    static CStopWatch rotTimer;
    
    //当前时间 * 60s
    float yRot = rotTimer.GetElapsedSeconds() * 60.0f;
    
    //2.矩阵变量
    /*
     mTranslate: 平移矩阵
     
     mRotate: 旋转矩阵
     mModelview: 模型视图矩阵
     mModelViewProjection: 模型视图投影MVP
     */
    M3DMatrix44f mTranslate, mRotate, mModelview, mModelViewProjection;
    
    //创建一个4*4矩阵变量，将花托沿着Z轴负方向移动10个单位长度
    m3dTranslationMatrix44(mTranslate, 0.0f, 0.0f, -10.0f);
    
    //创建一个4*4矩阵变量，将花托在Y轴上渲染yRot度，yRot根据经过时间设置动画帧率
     m3dRotationMatrix44(mRotate, m3dDegToRad(yRot), 0.0f, 1.0f, 0.0f);
    
    //为mModerView 通过矩阵旋转矩阵、移动矩阵相乘，将结果添加到mModerView上
    m3dMatrixMultiply44(mModelview, mTranslate, mRotate);
    
    // 将投影矩阵乘以模型视图矩阵，将变化结果通过矩阵乘法应用到mModelViewProjection矩阵上
    //注意顺序: 投影 * 模型 != 模型 * 投影
     m3dMatrixMultiply44(mModelViewProjection, viewFrustum.GetProjectionMatrix(),mModelview);
  
    //绘图颜色
    GLfloat vBlack[] = { 0.2f, 0.2f, 0.7f, 1.0f };
    
    //通过平面着色器提交矩阵，和颜色。
    shaderManager.UseStockShader(GLT_SHADER_FLAT, mModelViewProjection, vBlack);
    //开始绘图
    torusBatch.Draw();
    
    
    // 交换缓冲区，并立即刷新
    glutSwapBuffers();
    glutPostRedisplay();
}

首先我们使用了定时器，其次glutPostRedisplay()也会触发glutDisplayFunc注册的这个RenderSence再次进行渲染，然后交换缓冲区显示。

变换后如下，球体沿着Z负方向，向屏幕更深出平移，然后沿Y轴定时旋转

改了一下颜色，吐槽：本来很流畅的效果转成GIF才能上传

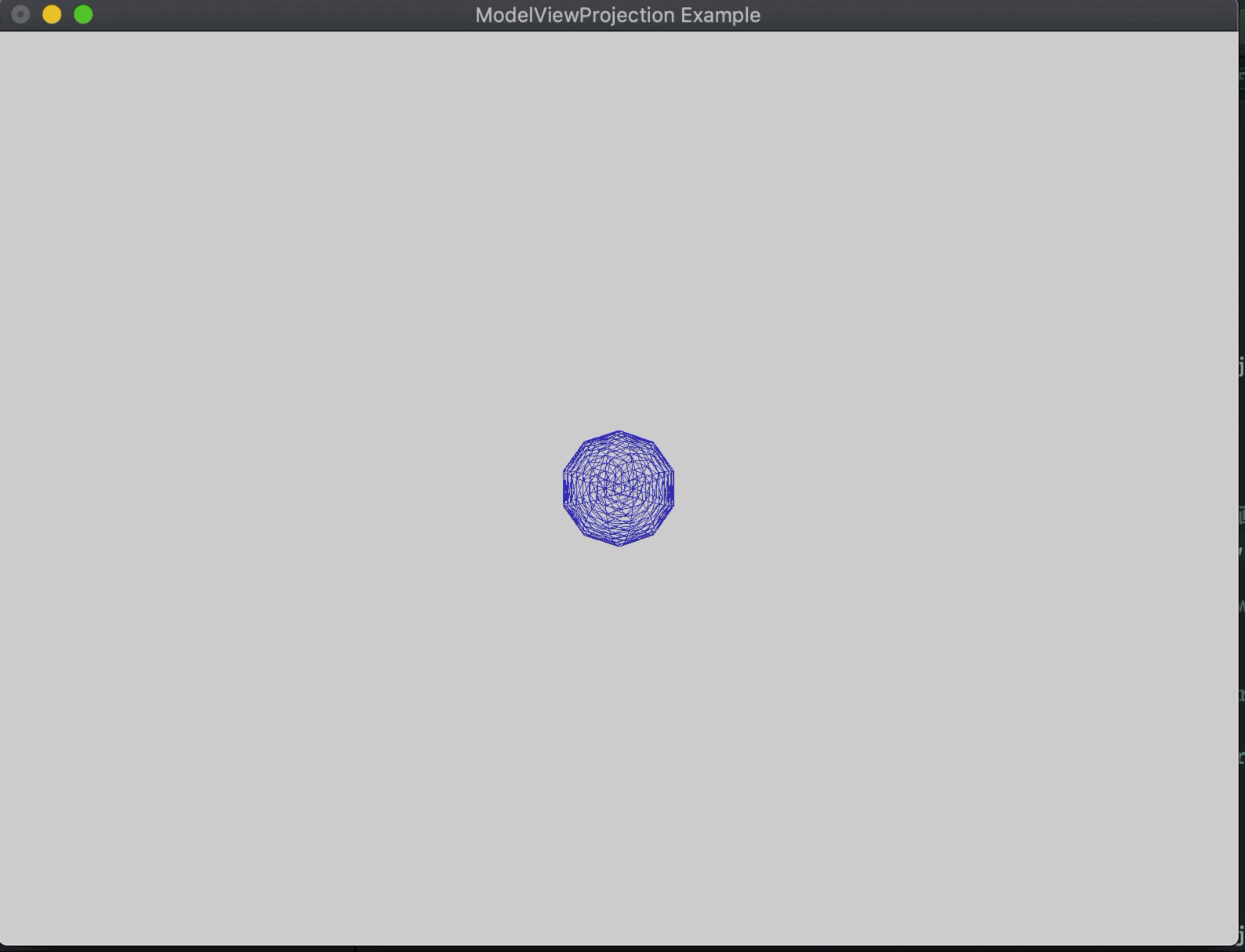
视图变换：

视图变换是应⽤到场景中的第一种变换, 它用来确定场景中的有利位置,在默认情况下, 透视投影中位于原点(0,0,0),并沿着 z 轴负方向进⾏观察 (向显示器内部”看过去”). 当观察者点位于原点(0,0,0) 时,就像在透视投影中⼀样.视图变换将观察者放在你希望的任何位置.并允许在任何方向上观察场景, 确定视图变换就像在场景中放置观察者并让它指向某⼀个方向; 从⼤大局上考虑, 在应⽤任何其他模型变换之前, 必须先应用视图变换. 这样做是因为, 对于视觉坐标系⽽言, 视图变换移动了当前的工作的坐标系; 后续的变化都会基于新调整的坐标系进⾏.

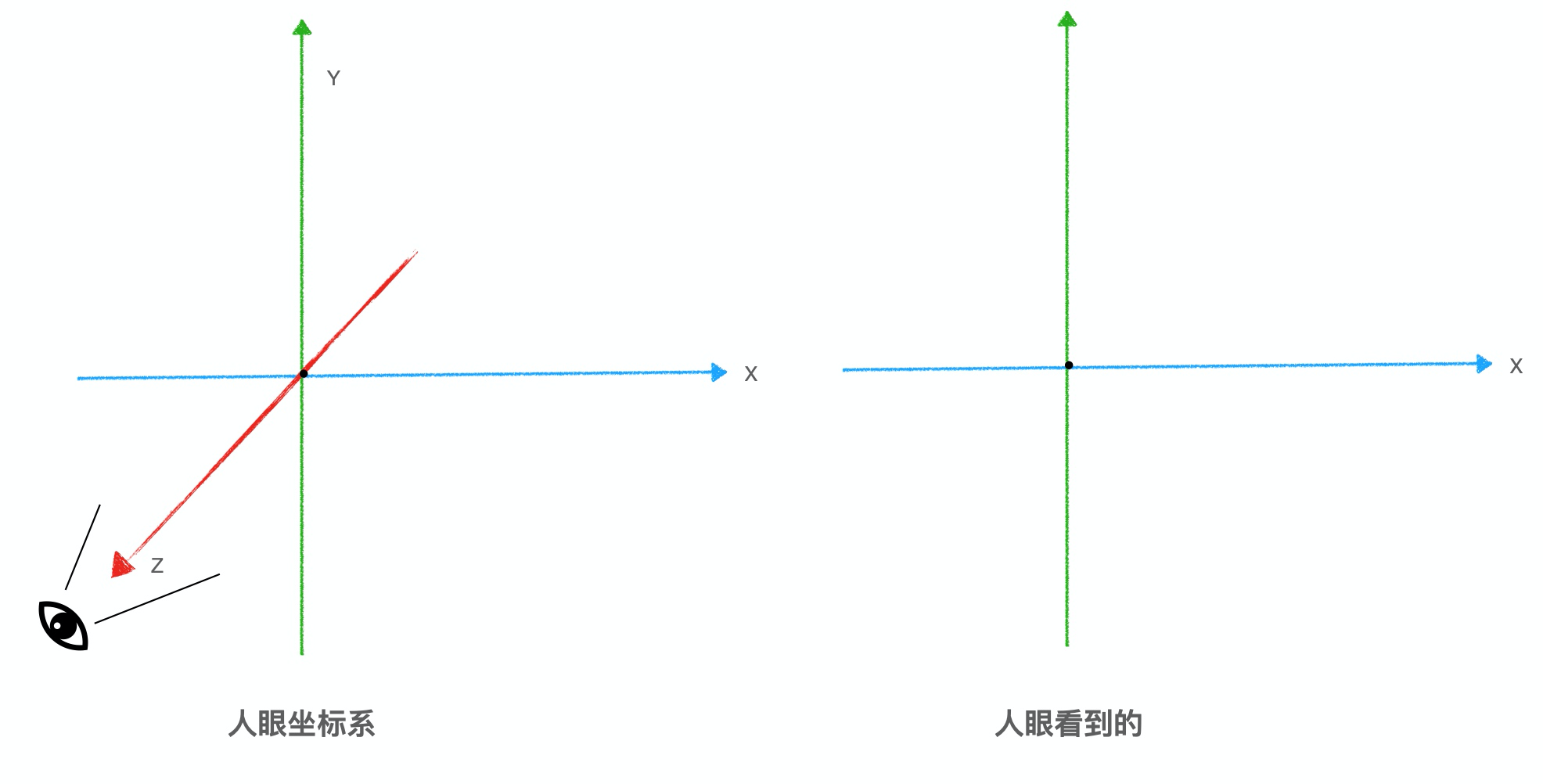
投影变换

下面是设置投影变换API，对应上图透视投影

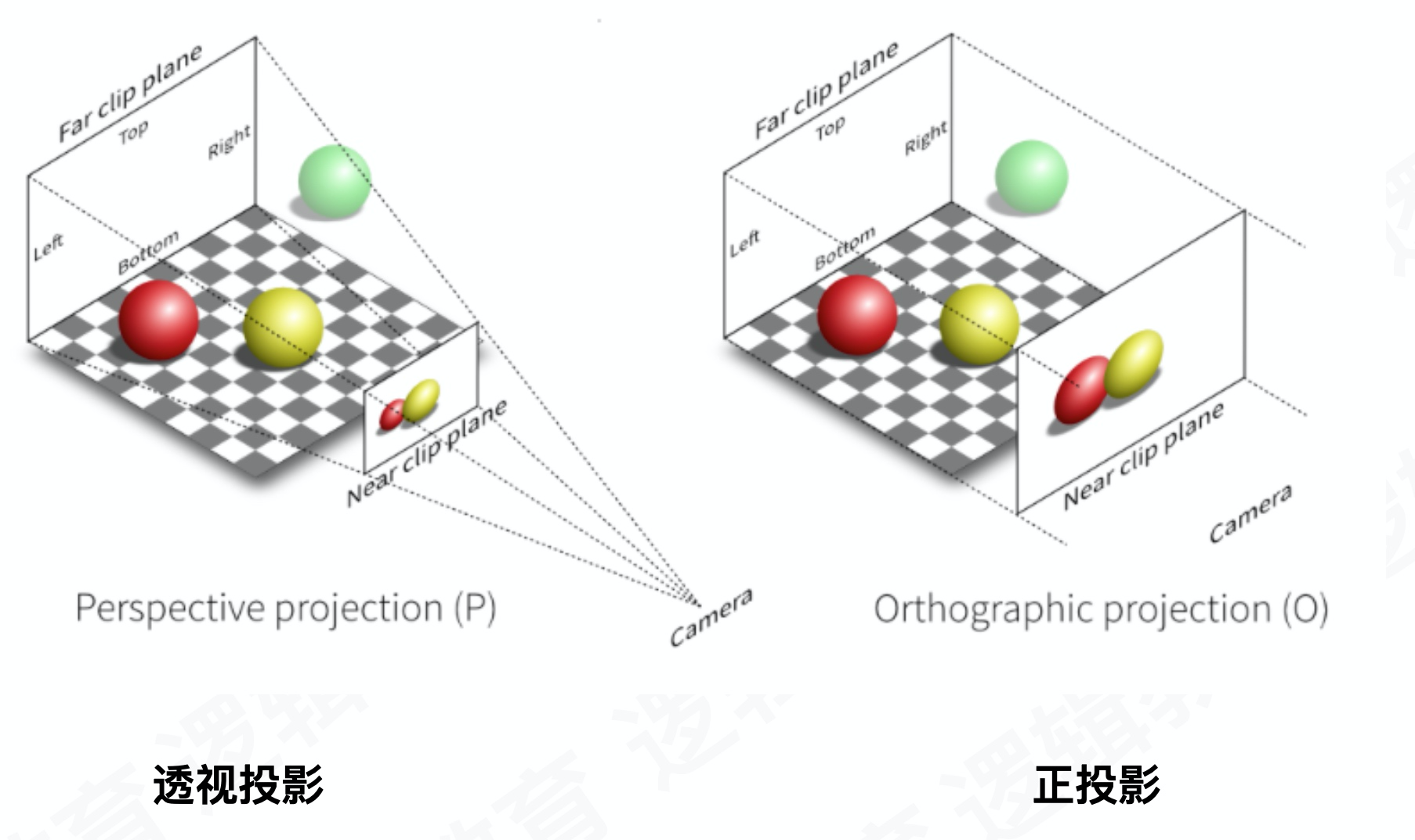
GLFrustum           viewFrustum;
// 通过调用SetPerspective函数我们可以设置投影变换
// fov 视野角度，影响视野范围
// fAspect 屏幕的宽高比
// fNear 到近端截面的距离
// fFar 到远端截面的面积
viewFrustum.SetPerspective(float fFov, float fAspect, float fNear, float fFar)

其他常用API

矩阵堆栈

//类型
GLMatrixStack::GLMatrixStack(int iStackDepth = 64);
//在堆栈顶部载⼊⼀个单元矩阵
void GLMatrixStack::LoadIdentity(void);
//在堆栈顶部载⼊任何矩阵 //参数:4*4矩阵
void GLMatrixStack::LoadMatrix(const M3DMatrix44f m);
//矩阵乘以矩阵堆栈顶部矩阵，相乘结果存储到堆栈的顶部
void GLMatrixStack::MultMatrix(const M3DMatrix44f);
//获取矩阵堆栈顶部的值 GetMatrix 函数 
//为了适应GLShaderMananger的使⽤用，或者获取顶部矩阵的副本
const M3DMatrix44f & GLMatrixStack::GetMatrix(void);
void GLMatrixStack::GetMatrix(M3DMatrix44f mMatrix);

堆栈操作API

//将当前矩阵压入堆栈(栈顶矩阵copy 一份到栈顶) 
void GLMatrixStack::PushMatrix(void);
//将M3DMatrix44f 矩阵对象压入当前矩阵堆栈
void PushMatrix(const M3DMatrix44f mMatrix);
//将GLFame 对象压⼊矩阵对象
void PushMatrix(GLFame &frame);
//出栈(出栈指的是移除顶部的矩阵对象) 
void GLMatrixStack::PopMatrix(void);

###为什么要使用堆栈矩阵？我们上面的综合变换只有一个球，而且模型视图矩阵是全局的。如果绘制比较多，没有push pop是不行的，否则别的变化都作用在mv上了，mv是全局的，本来不是你的也被影响了，push的意思就是，我先占用，等我绘制完了，pop是把我的变化从全局的mv的剔除掉，保持原来的模样，否则就乱套了，push pop就是为了把变化绘制了，还不影响整体环境，如果你不用push或者pop，那你自己精细算mv的数据也是可以的，比如mv+abc-897 绘制，完成mv-abc+897，这也可以，但是这只是规则变化，有规律可循，即使你熟悉非常牛逼，说一个复杂的图形怎么变化我都能计算出各个顶点的数值，变化完成之后我都可以复原，也可以自己算自己复原，但是，push 和 pop就搞定了。

GLFrame

//将堆栈的顶部压⼊入任何矩阵
void GLMatrixStack::LoadMatrix(GLFrame &frame);
//矩阵乘以矩阵堆栈顶部的矩阵。相乘结果存储在堆栈的顶部 void GLMatrixStack::MultMatrix(GLFrame &frame);
//将当前的矩阵压栈
void GLMatrixStack::PushMatrix(GLFrame &frame);

堆栈矩阵案例，综合使用了GLFrame的API和堆栈操作API

#include "GLTools.h"	// OpenGL toolkit
#include "GLMatrixStack.h"
#include "GLFrame.h"
#include "GLFrustum.h"
#include "GLBatch.h"
#include "GLGeometryTransform.h"
#include "StopWatch.h"

#include <math.h>
#ifdef __APPLE__
#include <glut/glut.h>
#else
#define FREEGLUT_STATIC
#include <GL/glut.h>
#endif



GLShaderManager		shaderManager;
GLMatrixStack		modelViewMatrix;
GLMatrixStack		projectionMatrix;
//观察者位置
GLFrame				cameraFrame;
//世界坐标位置
GLFrame             objectFrame;

//视景体，用来构造投影矩阵
GLFrustum			viewFrustum;

//三角形批次类
GLTriangleBatch     CC_Triangle;

//球
GLTriangleBatch     sphereBatch;
//环
GLTriangleBatch     torusBatch;
//圆柱
GLTriangleBatch     cylinderBatch;
//锥
GLTriangleBatch     coneBatch;
//磁盘
GLTriangleBatch     diskBatch;

GLGeometryTransform	transformPipeline;
M3DMatrix44f		shadowMatrix;

GLfloat vGreen[] = { 0.0f, 1.0f, 0.0f, 1.0f };
GLfloat vBlack[] = { 0.0f, 0.0f, 0.0f, 1.0f };

int nStep = 0;

// 将上下文中，进行必要的初始化
void SetupRC()
{
    //1.
    glClearColor(0.7f, 0.7f, 0.7f, 1.0f );
    shaderManager.InitializeStockShaders();
    
    //2.开启深度测试
    glEnable(GL_DEPTH_TEST);


    //3.将观察者坐标位置Z移动往屏幕里移动15个单位位置
    //表示离屏幕之间的距离 负数，是往屏幕后面移动；正数，往屏幕前面移动
    cameraFrame.MoveForward(-15.0f);

    //4.利用三角形批次类构造图形对象
    // 球
    /*
      gltMakeSphere(GLTriangleBatch& sphereBatch, GLfloat fRadius, GLint iSlices, GLint iStacks);
     参数1：sphereBatch，三角形批次类对象
     参数2：fRadius，球体半径
     参数3：iSlices，从球体底部堆叠到顶部的三角形带的数量；其实球体是一圈一圈三角形带组成
     参数4：iStacks，围绕球体一圈排列的三角形对数
     
     建议：一个对称性较好的球体的片段数量是堆叠数量的2倍，就是iStacks = 2 * iSlices;
     绘制球体都是围绕Z轴，这样+z就是球体的顶点，-z就是球体的底部。
     */
    gltMakeSphere(sphereBatch, 3.0, 10, 20);
    
    // 环面
    /*
     gltMakeTorus(GLTriangleBatch& torusBatch, GLfloat majorRadius, GLfloat minorRadius, GLint numMajor, GLint numMinor);
     参数1：torusBatch，三角形批次类对象
     参数2：majorRadius,甜甜圈中心到外边缘的半径
     参数3：minorRadius,甜甜圈中心到内边缘的半径
     参数4：numMajor,沿着主半径的三角形数量
     参数5：numMinor,沿着内部较小半径的三角形数量
     */
    gltMakeTorus(torusBatch, 3.0f, 0.75f, 15, 15);
    
    // 圆柱
    /*
     void gltMakeCylinder(GLTriangleBatch& cylinderBatch, GLfloat baseRadius, GLfloat topRadius, GLfloat fLength, GLint numSlices, GLint numStacks);
     参数1：cylinderBatch，三角形批次类对象
     参数2：baseRadius,底部半径
     参数3：topRadius,头部半径
     参数4：fLength,圆形长度
     参数5：numSlices,围绕Z轴的三角形对的数量
     参数6：numStacks,圆柱底部堆叠到顶部圆环的三角形数量
     */
    gltMakeCylinder(cylinderBatch, 2.0f, 2.0f, 3.0f, 15, 2);
    
    //锥
    /*
     void gltMakeCylinder(GLTriangleBatch& cylinderBatch, GLfloat baseRadius, GLfloat topRadius, GLfloat fLength, GLint numSlices, GLint numStacks);
     参数1：cylinderBatch，三角形批次类对象
     参数2：baseRadius,底部半径
     参数3：topRadius,头部半径
     参数4：fLength,圆形长度
     参数5：numSlices,围绕Z轴的三角形对的数量
     参数6：numStacks,圆柱底部堆叠到顶部圆环的三角形数量
     */
    //圆柱体，从0开始向Z轴正方向延伸。
    //圆锥体，是一端的半径为0，另一端半径可指定。
    gltMakeCylinder(coneBatch, 2.0f, 0.0f, 3.0f, 13, 2);
    
    // 磁盘
    /*
    void gltMakeDisk(GLTriangleBatch& diskBatch, GLfloat innerRadius, GLfloat outerRadius, GLint nSlices, GLint nStacks);
     参数1:diskBatch，三角形批次类对象
     参数2:innerRadius,内圆半径
     参数3:outerRadius,外圆半径
     参数4:nSlices,圆盘围绕Z轴的三角形对的数量
     参数5:nStacks,圆盘外网到内围的三角形数量
     */
    gltMakeDisk(diskBatch, 1.5f, 3.0f, 13, 3);
}



void DrawWireFramedBatch(GLTriangleBatch* pBatch)
{
    //----绘制图形----
    //1.平面着色器，绘制三角形
    shaderManager.UseStockShader(GLT_SHADER_FLAT, transformPipeline.GetModelViewProjectionMatrix(), vGreen);
     //传过来的参数，对应不同的图形Batch
    pBatch->Draw();
    
    //---画出黑色轮廓---
    
    //2.开启多边形偏移
    glEnable(GL_POLYGON_OFFSET_LINE);
    //多边形模型(背面、线) 将多边形背面设为线框模式
    glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
    //开启多边形偏移(设置偏移数量)
    glPolygonOffset(-1.0f, -1.0f);
    //线条宽度
    glLineWidth(2.5f);
    
    //3.开启混合功能(颜色混合&抗锯齿功能)
    glEnable(GL_BLEND);
    //开启处理线段抗锯齿功能
    glEnable(GL_LINE_SMOOTH);
    //设置颜色混合因子
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
   
   //4.平面着色器绘制线条
    shaderManager.UseStockShader(GLT_SHADER_FLAT, transformPipeline.GetModelViewProjectionMatrix(), vBlack);
    
    pBatch->Draw();
    
    //5.恢复多边形模式和深度测试
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
    glDisable(GL_POLYGON_OFFSET_LINE);
    glLineWidth(1.0f);
    glDisable(GL_BLEND);
    glDisable(GL_LINE_SMOOTH);
}

//召唤场景
void RenderScene(void)
{
    //1.用当前清除颜色清除窗口背景
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT | GL_STENCIL_BUFFER_BIT);
    
    //2.模型视图矩阵栈堆，压栈
    modelViewMatrix.PushMatrix();
    
    //3.获取摄像头矩阵
    M3DMatrix44f mCamera;
    //从camereaFrame中获取矩阵到mCamera
    cameraFrame.GetCameraMatrix(mCamera);
    //模型视图堆栈的 矩阵与mCamera矩阵 相乘之后，存储到modelViewMatrix矩阵堆栈中
    modelViewMatrix.MultMatrix(mCamera);
    
    //4.创建矩阵mObjectFrame
    M3DMatrix44f mObjectFrame;
    //从ObjectFrame 获取矩阵到mOjectFrame中
    objectFrame.GetMatrix(mObjectFrame);
    //将modelViewMatrix 的堆栈中的矩阵 与 mOjbectFrame 矩阵相乘，存储到modelViewMatrix矩阵堆栈中
    modelViewMatrix.MultMatrix(mObjectFrame);
    
    
    //5.判断你目前是绘制第几个图形
    switch(nStep) {
        case 0:
            DrawWireFramedBatch(&sphereBatch);
            break;
        case 1:
            DrawWireFramedBatch(&torusBatch);
            break;
        case 2:
            DrawWireFramedBatch(&cylinderBatch);
            break;
        case 3:
            DrawWireFramedBatch(&coneBatch);
            break;
        case 4:
            DrawWireFramedBatch(&diskBatch);
            break;
    }
    
    //6. pop
    modelViewMatrix.PopMatrix();
    
    //7.
    glutSwapBuffers();
}




//上下左右，移动图形
void SpecialKeys(int key, int x, int y)
{
    if(key == GLUT_KEY_UP)
        objectFrame.RotateWorld(m3dDegToRad(-5.0f), 1.0f, 0.0f, 0.0f);
    
    if(key == GLUT_KEY_DOWN)
        objectFrame.RotateWorld(m3dDegToRad(5.0f), 1.0f, 0.0f, 0.0f);
    
    if(key == GLUT_KEY_LEFT)
        objectFrame.RotateWorld(m3dDegToRad(-5.0f), 1.0f, 1.0f, 1.0f);
    
    if(key == GLUT_KEY_RIGHT)
        objectFrame.RotateWorld(m3dDegToRad(5.0f), 1.0f, 1.0f, 1.0f);
    
    glutPostRedisplay();
}




//点击空格，切换渲染图形
void KeyPressFunc(unsigned char key, int x, int y)
{
    if(key == 32)
    {
        nStep++;
        
        if(nStep > 4)
            nStep = 0;
    }
    
    switch(nStep)
    {
        case 0:
            glutSetWindowTitle("Sphere");
            break;
        case 1:
            glutSetWindowTitle("Torus");
            break;
        case 2:
            glutSetWindowTitle("Cylinder");
            break;
        case 3:
            glutSetWindowTitle("Cone");
            break;
        case 4:
            glutSetWindowTitle("Disk");
            break;
    }
    
    glutPostRedisplay();
}


void ChangeSize(int w, int h)
{
    //1.视口
    glViewport(0, 0, w, h);
    
    //2.透视投影
    viewFrustum.SetPerspective(35.0f, float(w) / float(h), 1.0f, 500.0f);
    //projectionMatrix 矩阵堆栈 加载透视投影矩阵
    projectionMatrix.LoadMatrix(viewFrustum.GetProjectionMatrix());
    
    //3.modelViewMatrix 矩阵堆栈 加载单元矩阵
     modelViewMatrix.LoadIdentity();
    
    //4.通过GLGeometryTransform管理矩阵堆栈
    //使用transformPipeline 管道管理模型视图矩阵堆栈 和 投影矩阵堆栈
    transformPipeline.SetMatrixStacks(modelViewMatrix, projectionMatrix);
}


int main(int argc, char* argv[])
{
    gltSetWorkingDirectory(argv[0]);
    
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH | GLUT_STENCIL);
    glutInitWindowSize(800, 600);
    glutCreateWindow("Sphere");
    glutReshapeFunc(ChangeSize);
    glutKeyboardFunc(KeyPressFunc);
    glutSpecialFunc(SpecialKeys);
    glutDisplayFunc(RenderScene);
    
    GLenum err = glewInit();
    if (GLEW_OK != err) {
        fprintf(stderr, "GLEW Error: %s\n", glewGetErrorString(err));
        return 1;
    }
    
    
    SetupRC();
    
    glutMainLoop();
    
    
    
    return 0;
}

运行结果录屏：（吐槽：只能上传5M） (pic.027cgb.com/631296/bk/通…

简单阶段一下这份代码：

点击空格键触发void KeyPressFunc(unsigned char key, int x, int y)，切换标题和触发RenderSence
上面KeyPressFunc通过glutPostRedisplay();触发RenderSence渲染显示新的图形
点击上下左右键，触发void SpecialKeys(int key, int x, int y)，完成图形的旋转变化

可以看到分别移动图形都不会改变影响其他图形之前的状态，就是因为有栈的存在。

仿射变换API

//Rotate 函数angle参数是传递的度数，⽽而不不是弧度
void MatrixStack::Rotate(GLfloat angle,GLfloat x,GLfloat y,GLfloat z);
void MatrixStack::Translate(GLfloat x,GLfloat y,GLfloat z);
void MatrixStack::Scale(GLfloat x,GLfloat y,GLfloat z);

通过案例看OpenGL的基本图形变换和矩阵操作