贝叶斯滤波的详细推导 卡尔曼滤波的详细推导 贝叶斯滤波、卡尔曼滤波和粒子滤波的关系
第一讲 很有必要的绪论
第二讲 随机过程与主观概率
概率论和数理统计研究的随机变量只考虑独立性
随机过程的随机变量之间不独立,有相关性
主观概率学说=贝叶斯学派
大数定律学说=频率学派--要做随机实验来确定概率
随机实验要满足三个条件,①可重复性=随机变量之间相互独立
随机过程不能做随机实验,因为不独立
主观概率=先验概率,观测之前的概率
后验概率=“后测“概率,观测之后的概率
先验概率 通过贝叶斯公式 转换为后验概率
第三讲 贝叶斯滤波的三大概率
三大概率
- 先验概率:凭感觉经验猜;观测前的概率
- 后验概率:观测后的概率
- 似然概率:表面测量的误差
全概率公式:结果分解为原因
似然概率是传感器的精度,是客观存在的确定的概率 ;先验概率是自己实验前猜的,也是客观存在的确定的概率所以P(Tm=10.3)是一个定值(只与似然概率和先验概率有关,由全概率公式展开可知)
第六讲 随机过程贝叶斯滤波的推导
番外票
1傅里叶变换
推导使用的傅里叶变换指数的正负号和信号与系统的不一样,主要是因为这里使用的是概率论与数理统计中定义的特征函数,用正号的话,**求矩(求期望和方差)**比较方便.
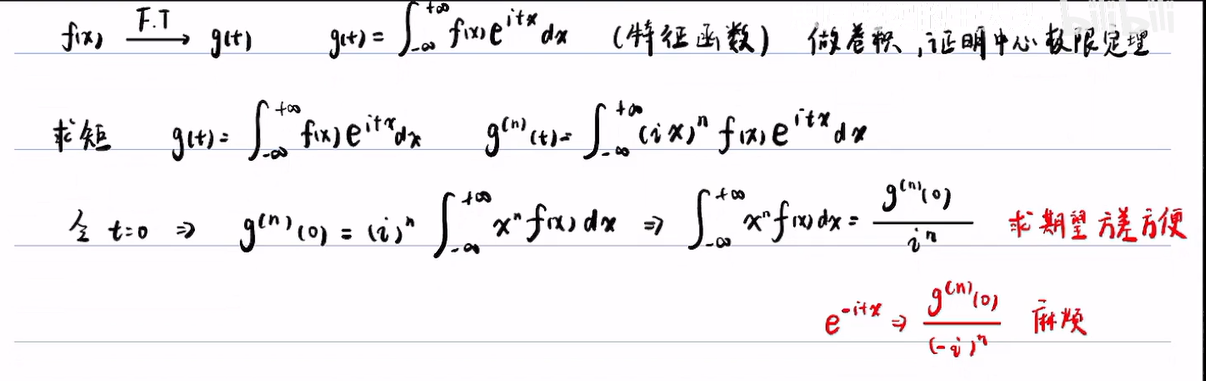
2第六讲的推导
预测步推导可以用卷积,但是也存在非线性下不好解的问题