归一化

ImmortalCoder
1,495 阅读6分钟

1. 基本概念

为了消除数据特征之间的量纲影响，需要对特征进行归一化处理，使得不同指标之间具有可比性。

归一化和标准化都属于四种 Feature scaling (特征缩放)，这四种分别是

  1. Rescaling (min-max normalization) 有时简称 normalization
x^` = \frac{x - min(x)} {max(x) - min(x)}
  1. Mean normalization
x^` = \frac{x - mean(x)} {max(x) - min(x)}
  1. Standardization (Z-score normalization)
x^` = \frac{x - mean(x)} {\sigma}
  1. Scaling to unit length
x^` = \frac{x - mean(x)} {\sigma}

在一些博客中，一般把第一种叫做归一化，第三种叫做标准化。

注：以下归一化的翻译来自《百面机器学习》

对数值类型的特征做归一化可以将所有的特征都统一到一个大致相同的数值区间内，常用的为一下两种：

1.1 线性函数归一化 (min-max normalization)

对原始数据进行线性变换，将结果映射到 [0, 1] 的范围内，实现对原始数据的等比缩放

x^` = \frac{x - mean(x)} {max(x) - min(x)}

此方法对数值进行归一，丢失了数据的分布信息，对数据之间的距离没有得到较好的保留，但保留了权值。

适用场景：

  1. 小数据 / 固定的数据
  2. 不涉及距离度量、协方差计算，数据不符合正态分布
  3. 进行多指标综合评价

缺点：

  1. 丢失样本键的距离信息
  2. 鲁棒性较差，当有新样本加入时最大值和最小值容易受到异常点的影响

目的：消除量纲，将各个指标的数据纳入到综合评价中。

1.2 零均值归一化 (Z-score normalization)

将原始数据映射到均值为 0、标准差为 1 的分布上。

x^` = \frac{x - \mu} {\sigma}

这个方法经常用于确保数据点没有因为特征的基本性质而产生较大差异，即确保数据处于同一数量级（同一量纲），提高不同特征数据的可比性。

适用场景：在分类、聚类算法中，需要使用距离来度量相似性的时候，或者使用 PCA 技术进行降维的时候，

缺点：丢失样本键的权重信息，分母是间接代表权重的标准差。

目的：便于后续的梯度下降和激活函数对数据的处理。因为零均值归一化后，数据以 0 为中心左右分布 (不一定对称)，而函数 Sigmoid、Tanh、Softmax 等都是以 0 为中心的左右分布 (不一定对称)。

1.3 两者的联系

  1. 联系：归一化广义上是包含标准化的，Z-Score 方法也是归一化的方法之一，在这里主要是从狭义上，区分两者
  2. 本质上都是进行特征提取，方便最终的数据比较认识，都通过先平移(分子相减)后缩放(分母)进行进行提取
  3. 都是为了缩小范围，便于后续的数据处理.
  4. 作用：(重点) i) 速度上：加快梯度下降，损失函数收敛 ii) 质量上：提升模型精度，也就是分类准确率 (消除不同量纲，便于综合指标评价，提高分类准确率) iii) 稳定性上：防止梯度爆炸 (消除因为数据输入差距 (1 和 2000) 过大，而带来的输出差距过大 (0.8，999)，进而在 反向传播的过程当中，导致梯度过大 (因为反向传播的过程当中进行梯度计算，会使用的之前对应层的输入 x)，从而形成梯度爆炸)

1.4 Softmax 对数归一化

S_i = \frac{e^i} {\sum_{i}e^i}

1.5 L2 归一化

向量 X = (x_1, x_2,...,x_n) 的 L2 范数为：

norm(x) = \sqrt{x_1^2 + x_2^2 +...+x_n^2}

要使得 x 归一化到单位 L2 范数，即建立一个从 x 到 x` 的映射，使得 x` 的 L2 范数为 1，即：

\begin{equation}\begin{split} 1=norm(x`)&=\frac{\sqrt{x_1^2 + x_2^2 +...+x_n^2}}{norm(x)} \\ &=\frac{\sqrt{x_1^2 + x_2^2 +...+x_n^2}}{norm(x)^2} \\ &=\sqrt{(\frac{x_1}{norm(x)})^2 + (\frac{x_2}{norm(x)^2}) + ...+(\frac{x_n}{norm(x)})^2}\\ & = \sqrt{x_1^2 + x_2^2 +...+x_n^2}\end{split}\end{equation}

即：

x_i^{`} = \frac{x_i}{norm(x)}

2. 为什么要对数值型特征做归一化

归一化可以提高梯度下降法求解最优解的速度。

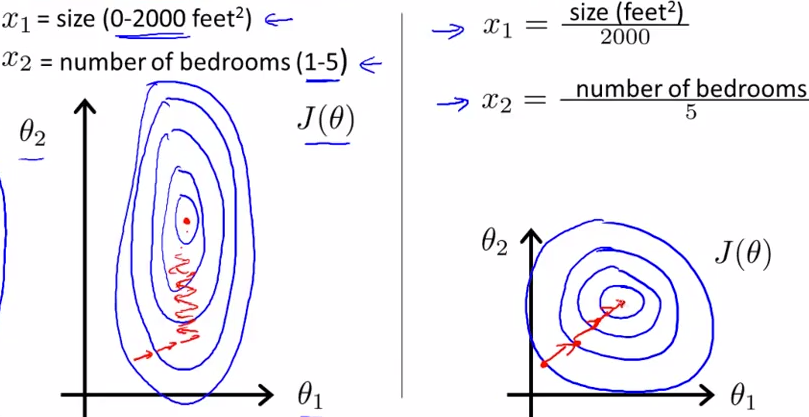
蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征 X1 和 X2 的区间相差非常大，X1 区间是 [0, 2000]，X2 区间是 [1, 5]，像这种有的数据那么大，有的数据那么小，两类之间的幅度相差这么大，其所形成的等高线非常尖。当使用梯度下降法寻求最优解时，很有可能走“之字型”路线（垂直等高线走），从而导致需要迭代很多次才能收敛；

而右图对两个原始特征进行了归一化，其对应的等高线显得很圆，在梯度下降进行求解时能较快的收敛。

因此如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。

3. 归一化的应用

需要归一化的模型：

  1. 基于距离计算的模型：KNN。
  2. 通过梯度下降法求解的模型：线性回归、逻辑回归、支持向量机、神经网络。
  • logistic regression 模型：逻辑回归，虽然迭代若几次没有影响，但实际当中远不止若干次，这样就会导致逻辑回归模型的目标函数过于扁化，导致梯度很难下降，不容易得到较好的模型参数。
  • SVM 模型：因为涉及到向量 / 数据的距离 (向量之间差异过大 / 过小，就会导致最佳分离超平面可能会由最大 / 远或者最小 / 近的几个向量支配，导致鲁棒性较差，因此需要进行标准化—可以保留向量间的模型)。
  • Neural Network 模型：初始输入值过大，反向传播时容易梯度爆炸。
  • SGD：加快梯度下降。

其中基于距离计算的模型，如果一个特征值域范围非常大，那么距离的计算就主要取决于这个特征，从而与实际情况相悖，比如实际情况是值域范围小的特征更重要。

不需要归一化的模型：

  1. 0 / 1 取值的特征通常不需要归一化，归一化会破坏它的稀疏性

  2. 概率模型不需要归一化，它们不关心变量值，而关心变量的分布、变量之间的条件概率。这类模型像决策树、随机森林。

  3. 基于平方损失的最小二乘法 OLS 不需要归一化 (因为本质上是一个抛物线,强凸函数,下降速度快.)

由于数值缩放不影响分裂点位置，对树模型的结构不造成影响。

按照特征值进行排序的，排序的顺序不变，那么所属的分支以及分裂点就不会有不同。而且，树模型是不能进行梯度下降的，因为构建树模型（回归树）寻找最优点时是通过寻找最优分裂点完成的，因此树模型是阶跃的，阶跃点是不可导的，并且求导没意义，也就不需要归一化。

avatar
文章
阅读
粉丝